
Алгоритмы сортировки данных (Понятие алгоритма сортировки)
Содержание:
ВВЕДЕНИЕ
Успешное выполнение большинством специалистов своих функциональных обязанностей в настоящее время во многом определяется умелым использованием персональных компьютеров, средств коммуникаций, профессиональных пакетов прикладных программ, различного рода интеллектуальных информационных технологий. Процессы информатизации общества обусловили необходимость формирования у студентов знаний в области информатики и компьютеризации управленческих процессов.
Одно из широко используемых понятий информатики определяет ее как науку, изучающую общие свойства информации, а также методы, процессы, технические и программные средства для ее автоматизированной обработки.
Сам термин «информатика» (informatique) возник в 60-х годах во Франции для определения области исследований, связанных с автоматизацией обработки информации с помощью электронных вычислительных машин (ЭВМ). Этот термин был образован слиянием слов information (информация) и automatique (автоматика) для обозначения информационной автоматики или автоматизированной переработки информации.
Данная курсовая работа состоит из двух частей: теоретической и практической.
Целью теоретической части курсовой работы является ознакомление с алгоритмами сортировки, попытка проанализировать их и осветить каждый из них.
В практической части курсовой работы с помощью пакетов прикладных программ (ППП) будут решены и описаны следующие задачи:
-
- создание таблиц и заполнение таблиц данными;
- применение математических формул для выполнения запросов в ППП;
- построение графиков.
Краткие характеристики ПК и программного обеспечения, использованных для выполнения и оформления курсовой работы:
- Процессор: Inter Core i7-3612QM 2.10GHz;
- Оперативная память: RAM 8,0Gb;
- Жесткий диск: SDD 126Gb;
- Видеокарта: Intel HD Graphics 4000;
- Клавиатура: Logitech G15;
- Мышь: Logitech G9.
Программные средства: операционная система Windows 10, пакет прикладных программ – MS Office 2019 (из него использованы для выполнения курсовой работы: текстовый процессор MS Word 2019, табличный процессор MS Excel 2019).
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. Понятие алгоритма сортировки
Алгоритм – это точно определенная последовательность действий, которую необходимо выполнить над исходными данными для достижения решения задачи.
Слово «алгоритм» происходит от имени узбекского математика девятого века Аль-Харезми, который сформулировал правило четырёх арифметических действий над многозначными числами. В дальнейшем это слово стало использоваться не только в математике, а фактически любую последовательность действий, приводящих к конечному результату, стали называть алгоритмом, а каждое действие шагом алгоритма. Алгоритм обладает рядом свойств, связанных с необходимостью выполнения определенных требований к процессу вычисления. Это следующие свойства: определённость, массовость, результативность, дискретность.
Определённость алгоритма означает, что каждый шаг алгоритма должен быть точен, общепонятен, и исключать возможность различного толкования, другими словами, алгоритм должен быть таким, чтобы его мог повторить любой пользователь.
Массовость заключается в том, что алгоритм предназначен для решения целого класса задач, которые отличаются только своими входными условиями.
Результативность означает, что пошаговый процесс решения задачи в соответствии с алгоритмом должен заканчиваться через определенное конечное число шагов.
Формы представления алгоритма:
- Словесная форма;
- Словесно-аналитическая форма;
- В виде блок-схемы (графическое изображение алгоритма);
- В виде программы на алгоритмическом языке программирования.
Виды алгоритмических структур:
-
- Линейный алгоритм, в которой все команды выполняются последовательно одна за другой.
- Разветвляющийся, в которой в зависимости от условия выполнения либо одна серия команд, либо другая.
- Циклический, в которой многократно повторяется некоторый участок алгоритма.
Первое поколение алгоритмических языков - конец 1950-х начало 1960-х. Совершенствовались ассемблерные языки. В настоящее время они применяются для создания драйверов оборудования ПК.
Второе поколение – 60-е годы. В это время появляются универсальные языки высшего уровня: фортран, алгол, кобол, обеспечивающие создание программ для решения задач различного класса.
Третье поколение. С начала 1970-х годов начался переход на создание больших программных комплексов. Они в основном применяются для проектирования приложений баз данных и средств визуального программирования.
В середине 1990-х – четвертое поколение языков программирования, назначение которых для образования инструкции текст программ на универсальном языке программирования. Система четвертого поколения имеет открытую архитектуру и поддерживает значительное число программных продуктов.
Языки программирования:
- Бейсик отличается встроенными математическими функциями и простыми языковыми конструкциями.
- Паскаль предназначен для решения вычислительных и информационно-логических задач.
- Си ++ был разработан для облегчения процесса переноса программного обеспечения с одной ЭВМ на другую.
- Ада ориентирован для применения в системах реального времени и предназначен для разработки программного обеспечения встроенных вычислительных систем.
- Java (джава) предназначен для создания надёжных, переносимых, распределённых сетевых программных приложений, работающих в архитектуре клиент–сервер, а также удобен для администраторов сети.
- Другим объектно-ориентировочным языком является язык Delphi (дельпхи). Обеспечивает взаимодействие с базами данных, создание различных видов баз, а также работу экономических программ и сети интернет.
Алгоритм сортировки — это алгоритм для упорядочения элементов в списке. В случае, когда элемент списка имеет несколько полей, поле по которому производится сортировка, называется ключом сортировки. На практике, в качестве ключа часто выступает число, а в остальных полях хранятся какие-либо данные, никак не влияющие на работу алгоритма.
Пожалуй, никакая другая проблема не породила такого количества разнообразнейших решений, как задача сортировки. Существует ли некий «универсальный», наилучший алгоритм? Вообще говоря, нет. Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом.
Сортировка применяется во всех без исключения областях программирования, будь то базы данных или математические программы.
Практически каждый алгоритм сортировки можно разбить на три части:
- сравнение, определяющее упорядоченность пары элементов;
- перестановку, меняющую местами пару элементов;
- собственно сортирующий алгоритм, который осуществляет сравнение и перестановку элементов до тех пор, пока все элементы множества не будут упорядочены.
Подобными свойствами обладают и те алгоритмы сортировки, которые рассмотрены ниже. Они отобраны из множества алгоритмов, потому что, во-первых, наиболее часто используются, а во-вторых, потому что большинство остальных алгоритмов является различными модификациями описанных здесь.
Основные виды сортировок:
Сортировка пузырьком (англ. bubble sort) — простой алгоритм сортировки. Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При проходе алгоритма, элемент, стоящий не на своём месте, «всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма.
Сортировка методом пузырька имеет сложность O(n2). Для понимания и реализации это — простейший алгоритм сортировки, но эффективен он лишь для небольших массивов.
Пример реализации алгоритма (язык Pascal):
for i := n - 1 downto 1 do
for j := 1 to i do
if a[j] > a[j+1] then
begin
t := a[j];
a[j] := a[j+1];
a[j+1] := t;
end;
Сортировка перемешиванием (шейкер-сортировка) — разновидность пузырьковой сортировки. Отличается тем, что просмотры элементов выполняются один за другим в противоположных направлениях, при этом большие элементы стремятся к концу массива, а маленькие — к началу.
Лучший случай для этой сортировки — отсортированный массив (О(n)), худший — отсортированный в обратном порядке (O(n²)).
Сортировка методом вставок (англ. insertion sort) — простой алгоритм сортировки. Хотя этот метод сортировки намного менее эффективен чем более сложные алгоритмы (такие как быстрая сортировка), у него есть ряд преимуществ:
- прост в реализации
- эффективен на небольших наборах данных
- эффективен на наборах данных, которые уже частично отсортированы
- это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы)
- может сортировать список по мере его получения
На каждом шаге алгоритма, мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированном списке, до тех пор, пока набор входных данных не будет исчерпан. Выбор очередного элемента, выбираемого из исходного массива — произволен, может использоваться практически любой алгоритм выбора.
Сортировка подсчётом — алгоритм сортировки массива, при котором подсчитывается число одинаковых элементов. Алгоритм выгодно применять, когда в массиве много элементов, но все они достаточно малы.
Описание алгоритма. Идея сортировки указана в её названии — нужно подсчитывать число элементов, а затем выстраивать массив. Пусть, к примеру, имеется массив A из миллиона натуральных чисел, меньших 100. Тогда можно создать вспомогательный массив B из 99 (1..99) элементов, «пробежать» весь исходный массив и вычислять частоту встречаемости каждого элемента — то есть если A[i]=a, то B[a] следует увеличить на единицу. Затем «пробежать» счетчиком i массив B, записывая в массив A число i B[i] раз.
Сортировка слиянием (англ. merge sort) — алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например — потоки) в определённом порядке. Эта сортировка — хороший пример использования принципа «разделяй и властвуй».
Алгоритм был изобретён Джоном фон Нейманом в 1945 году.
Цифровая сортировка (англ. pigeonhole sort) обладает линейной вычислительной сложностью (О(n)), что является лучшей возможной производительностью для алгоритма сортировки, так как в любом таком алгоритме каждый сортируемый элемент необходимо просмотреть хотя бы однажды. Однако, применение алгоритма цифровой сортировки целесообразно лишь тогда, когда сортируемые предметы имеют (или их можно отобразить в) диапазон возможных значений, который достаточно мал по сравнению с сортируемым списком. Эффективность алгоритма падает всякий раз, когда несколько различных элементов попадает в одну ячейку. Необходимость сортировки внутри ячеек лишает алгоритм смысла, так как каждый элемент придётся просматривать более одного раза. Так что, для простоты и с целью отличить «классическую» цифровую сортировку от её многочисленных вариантов, укажем, что подсчёт должен быть обратимым: если два элемента попадают в одну ячейку, то они должны иметь одинаковое значение. Несколько элементов с одним значением в одной ячейке не портят картину — их можно просто вставить в отсортированный список рядом, один за другим (это позволяет применять цифровую сортировку в качестве устойчивой).
Алгоритм цифровой сортировки действует следующим образом:
- Создаём массив изначально пустых «ячеек», по одной для каждой величины из диапазона ключей.
- Просматриваем изначальный массив, помещая каждый его элемент в свою ячейку.
- Проходим по массиву ячеек в нужном порядке и переносим элементы из непустых ячеек обратно в первоначальный массив.
Эффективность этого алгоритма сильно зависит от плотности элементов в массиве ячеек. Если элементов этого массива намного больше, чем сортируемых предметов, то шаги 1 и 3 будут относительно медленными.
Сортировку подсчётом применяют редко, потому что её требования редко удовлетворяются, и часто бывает проще применить другие, более гибкие и почти такие же быстрые алгоритмы сортировки. В особенности, блочная сортировка является более практичным вариантом сортировки подсчётом. В некотором роде, быстрая сортировка представляет собой обобщённую сортировку подсчётом (всего с двумя ячейками в каждый момент времени).
Поразрядная сортировка — быстрая устойчивая сортировка за линейное время, использовалась в устройствах для сортировки перфокарт. Пригодна для сортировки любых элементов, состоящих из цепочек над фиксированным алфавитом, на котором задано отношение сравнения. Для сортировки следует применять любой устойчивый алгоритм, используя в качестве ключа сначала младшую букву, затем повторять этот процесс для старших букв.
Сортировка методом выбора (англ. selection sort) — алгоритм сортировки, относящийся к неустойчивым алгоритмам сортировки. На массиве из n элементов имеет время выполнения в худшем, среднем и лучшем случае Θ(n2), предполагая, что сравнения делаются за постоянное время.
Шаги алгоритма:
- находим минимальное значение в текущем списке
- производим обмен этого значения со значением на первой позиции
- теперь сортируем хвост списка, исключив из рассмотрения уже отсортированный первый элемент.
Пирамидальная сортировка сильно улучшает базовый алгоритм, используя структуру данных ключа для ускорения нахождения и удаления минимального элемента.
Существует также двунаправленный вариант сортировки методом вставок, в котором на каждом проходе отыскивается и устанавливается на своё место и минимальное, и максимальное значения.
Сортировка методом Шелла. Идея алгоритма состоит в обмене элементов, расположенных не только рядом, как в сортировке методом вставок, но и далеко друг от друга, что значительно сокращает общее число операций перемещения элементов.
Для примера возьмем файл из 16 элементов. Сначала просматриваются пары с шагом 8. Это пары элементов 1-9, 2-10, 3-11, 4-12, 5-13, 6-14, 7-15, 8-16. Если значения элементов в паре не упорядочены по возрастанию, то элементы меняются местами. Назовем этот этап 8-сортировкой. Следующий этап — 4-сортировка, на котором элементы в файле делятся на четверки: 1-5-9-13, 2-6-10-14, 3-7-11-15, 4-8-12-16. Выполняется сортировка в каждой четверке.
Следующий этап — 2-сортировка, когда элементы в файле делятся на 2 группы по 8: 1-3-5-7-9-11-13-15 и 2-4-6-8-10-12-14-16. Выполняется сортировка в каждой восьмерке. Наконец весь файл упорядочивается методом вставок. Поскольку дальние элементы уже переместились на свое место или находятся вблизи от него, этот этап будет значительно менее трудоемким, чем при сортировке вставками без предварительных «дальних» обменов.
Анализ алгоритма сортировки Шелла. Время выполнения сортировки пропорционально n1.2. Эта зависимость значительно лучше квадратичной зависимости n2, которой подчиняется большинство простых алгоритмов сортировки.
Пример реализации
procedure sort_shell (var a:array of word);
var
bis,i,j,k:longint;
h:word;
begin
bis:=high(a);
k:=bis shr 1;
While k>0 do
Begin
For i:=0 To bis-k do
begin
j:=i;
While (j>=0) And (a[j]>a[j+k]) do
begin
h:=a[j];
a[j]:=a[j+k];
a[j+k]:=h;
dec(j,k);
end;
end;
k:=k shr 1;
End;
End;
Пирамидальная сортировка — алгоритм сортировки, работающий в худшем, в среднем и в лучшем случае (т.е. гарантированно) за О(n log n) операций при сортировке n элементов.
Алгоритм:
Сортировка пирамидой использует сортирующее дерево. Сортирующее дерево – это такое двоичное дерево, у которого выполнены условия:
- Каждый лист имеет глубину либо d либо d-1
- Значение в любой вершине больше, чем значения ее потомков.
Удобная структура данных для сортирующего дерева – такой массив Array, что Array[1] – элемент в корне, а потомки элемента Array[i] - Array[2i] и Array[2i+1].
Алгоритм сортировки будет состоять из двух основных шагов:
1. Выстраиваем элементы массива в виде сортирующего дерева:
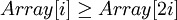
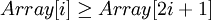
при 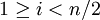
Этот шаг требует О(n) операций.
2. Будем удалять элементы из корня по одному за раз и перестраивать дерево. Т.е. на первом шаге обмениваем Array[1] и Array[n], преобразовываем Array[1], Array[2], ... , Array[n-1] в сортирующее дерево. Затем переставляем Array[1] и Array[n-1], преобразовываем Array[1], Array[2], ... , Array[n-2] в сортирующее дерево. Процесс продолжается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда Array[1], Array[2], ... , Array[n] - упорядоченная последовательность.
Этот шаг требует О(n log n) операций.
Быстрая сортировка (англ. quicksort) — широко известный алгоритм сортировки, разработанный английским информатиком Чарльзом Хоаром. Даёт в среднем O(n log n) сравнений при сортировке n элементов. В худшем случае, однако, получается O(n2) сравнений. Обычно на практике быстрая сортировка значительно быстрее, чем другие алгоритмы с оценкой O(n log n), по причине того, что внутренний цикл алгоритма может быть эффективно реализован почти на любой архитектуре, и на большинстве реальных данных можно найти решения, которые минимизируют вероятность того, что понадобится квадратичное время.
Интересно, что Хоар разработал этот метод применительно к машинному переводу: дело в том, что в то время словарь хранился на магнитной ленте, и если отсортировать все слова в тексте, их переводы можно получить за один прогон ленты.
Алгоритм. Быстрая сортировка использует стратегию «разделяй и властвуй». Шаги алгоритма таковы:
- Выбираем в массиве некоторый элемент, который будем называть опорным элементом.
- Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него.
- Рекурсивно сортируем подсписки, лежащие слева и справа от опорного элемента.
Базой рекурсии являются списки, состоящие из одного или двух элементов, которые уже отсортированы. Алгоритм всегда завершается, поскольку за каждую итерацию он ставит по крайней мере один элемент на его окончательное место.
При выборе опорного элемента из данного диапазона случайным образом, худший случай становится очень маловероятным и ожидаемое время выполнения алгоритма сортировки - O(n log n).
ПРАКТИЧЕСКАЯ ЧАСТЬ
2. Практическое задание
Фирма ООО «Стройдизайн» осуществляет деятельность, связанную с выполнением работ по ремонту помещений. Прайс-лист на выполняемые работы приведен на таблице 1. Данные о заказанных работах указаны на таблице 2.
Таблица 1. Прайс-лист на выполняемые работы
|
Наименование работы |
Единица измерения |
Цена за ед. изм., руб. |
|---|---|---|
|
Замена батарей |
шт. |
250 |
|
Замены ванны |
шт. |
210 |
|
Замена труб |
м |
240 |
|
Наклейка обоев |
м2 |
50 |
|
Настилка паркета |
м2 |
75 |
|
Побелка потолка |
м2 |
15 |
Таблица 2. Данные о поступившем заказе
|
Наименование работы |
Единица измерения |
Объем выполняемых работ |
Цена за ед. изм., руб. |
Стоимость работ, руб. |
|
Замена батарей |
шт. |
4 |
||
|
Наклейка обоев |
м2 |
20 |
||
|
Замена труб |
м |
4 |
||
|
Настилка паркета |
м2 |
15 |
- Построить таблицы по приведенным в приложениях данным.
- Выполнить расчет стоимости выполняемых работ по полученному заказу, данные расчета занести в таблицу (таблица 2).
- Организовать межтабличные связи для автоматического формирования счета, выставляемого клиенту для оплаты выполняемых работ.
- Сформировать и заполнить счет на оплату (таблица 3).
- Результаты расчета стоимости каждого вида работ по полученному заказу представить в графическом виде.
Таблица 3. Форма счета на оплату выполненных работ
|
ООО «Стройдизайн» СЧЕТ № 1 Дата __-__-20__ ФИО клиента _________________
Гл. бухгалтер ______________________________ |
||||||||||||||||||||||||||||||||||||||||||||||||
Для решения данной экономической задачи была выбрана среда табличного процессора MS Excel. Microsoft Office Excel является средством для создания электронных таблиц, которые обладают возможностями для проведения простых расчетов, как с использованием арифметических действий, так и с помощью встроенных функций; для построения разных типов диаграмм; для оформления полученных таблиц и т.д. Так же, MS Excel – программа, не требующая знаний программирования, достаточно проста в использовании для поиска результата данной задачи.
Порядок выполнения практического задания, следующий:
- Запустить табличный процессор MS Excel.
- Создать книгу с именем «Стройдизайн».
- Лист 1 переименовать в лист с названием Работа.
- На рабочем листе «Работа» MS Excel создать таблицу базового прайс-листа на выполняемые работы.
- Заполнить таблицу базового прайс-листа исходными данными (рисунок 1).
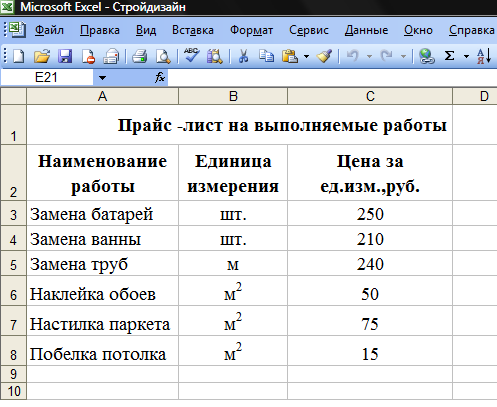
Рисунок 1. Структура таблицы «Прайс-лист» на рабочем листе Работа MS Excel
- Лист 2 переименовать в лист с названием Расчет стоимости выполняемых работ;
- Заполнить таблицу «Расчет стоимости выполняемых работ» исходными данными (рисунок 2);
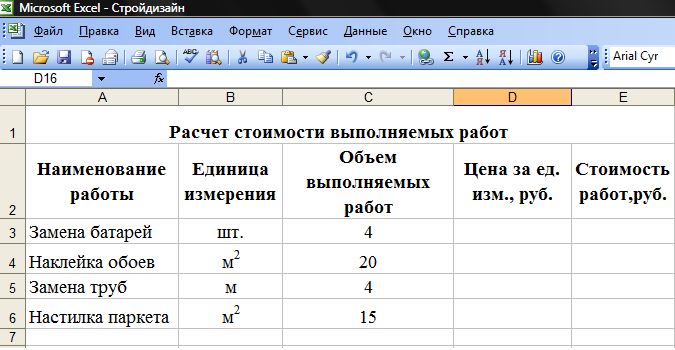
Рисунок 2. Структура таблицы «Расчет стоимости выполняемых работ»
- Заполнить графу Цена за ед. изм., руб. таблицы «Расчет стоимости выполняемых работ»
- Занести в ячейку D3 формулу:
=ЕСЛИ(A3=Работа!A3;Работа!C3;ЕСЛИ(A3=Работа!A4;Работа!C4;ЕСЛИ(A3=Работа!A5;Работа!C5;ЕСЛИ(A3=Работа!A6;Работа!C6;ЕСЛИ(A3=Работа!A7;Работа!C7;ЕСЛИ(A3=Работа!A8;Работа!C8))))))
10. Размножить введенную в ячейку D2 формулу для остальных ячеек
(с D3 по D5) данной графы (рисунок 3);
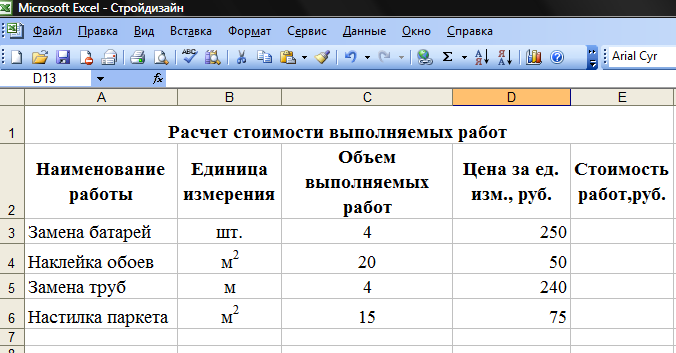
Рисунок 3. Структура таблицы «Расчет стоимости выполняемых работ»
11. Заполнить графу Стоимость работ, руб. таблицы «Расчет стоимости выполняемых работ» следующим образом:
-
- Занести в ячейку E3 формулу =C3*D3;
- Размножить введенную в ячейку E3 формулу для остальных ячеек (с E4 по E6) данной графы;
12. Таблица «Расчет стоимости выполняемых работ» автоматически заполнится (рисунок 4.);
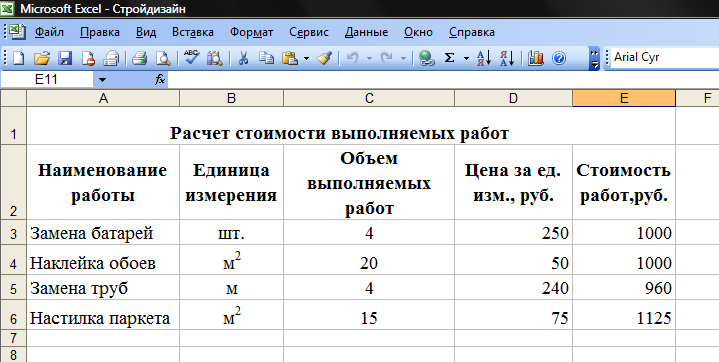
Рисунок 4. Структура таблицы «Расчет стоимости выполняемых работ»
13. Лист 3 переименовать в лист с названием Счет;
14. На рабочем листе «Счет» MS Excel создать форму счета на оплату выполненных работ (рисунок 5);
15. Путем создания межтабличных связей заполнить созданную форму полученными данными из таблицы «Расчет стоимости выполняемых работ»;
16. Заполнить графу ИТОГО формы счета на оплату выполненных работ следующим образом: в ячейку G16 ввести формулу =СУММ(G12:G15);
17. Заполнить графу НДС формы счета на оплату выполненных работ следующим образом: в ячейку G17 ввести формулу =G16*13%;
18. Заполнить графу СУММА С НДС формы счета на оплату выполненных работ следующим образом: в ячейку G18 ввести формулу =СУММ(G16:G17);
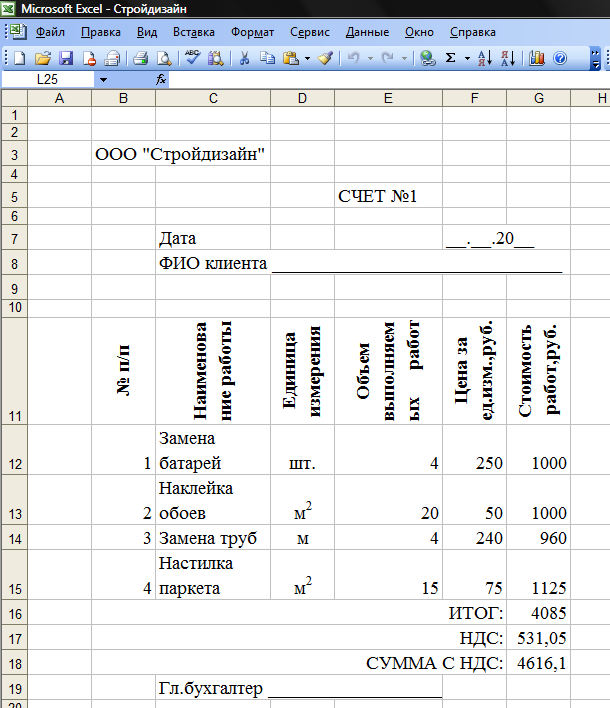
Рисунок 5. Структура таблицы «Счет»
19. Лист 4 переименовать в лист с названием График.
20. На рабочем листе «График» MS Excel создать сводную таблицу.
21. Путем создания межтабличных связей автоматически заполнить графы Наименование работы и Стоимость работ, руб. полученными данными из таблицы «Расчет стоимости выполняемых работ»
22. С помощью мастера диаграмм создать график.
23. Результаты вычислений представить графически (рисунок 6);
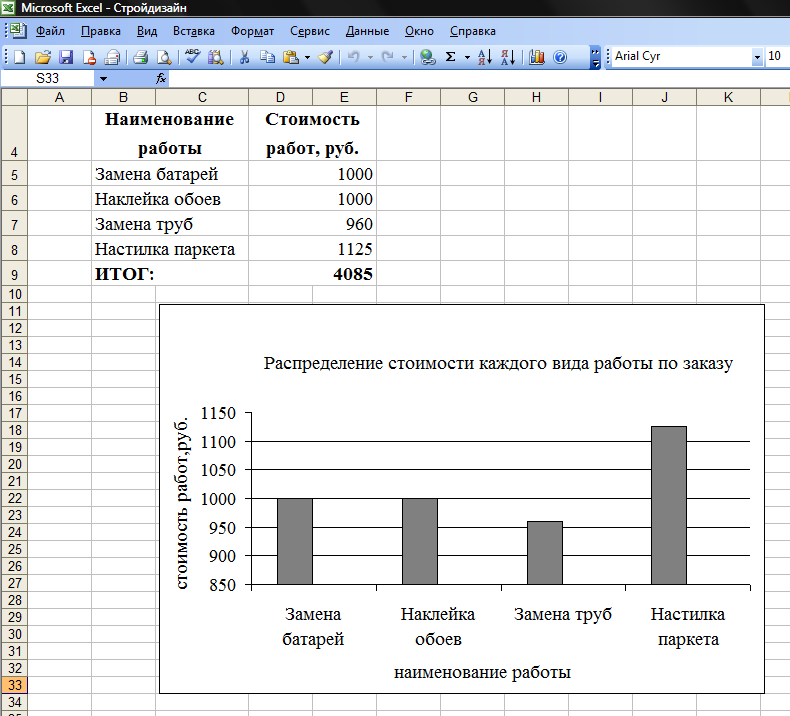
Рисунок 6. Сводная таблица и графическое представление результатов вычислений.
ЗАКЛЮЧЕНИЕ
Современную жизнь представить без современной техники просто невозможно.
Ни одна фирма не обходится без помощи компьютеров. Хранение данных, написание документов, составление графиков, таблиц, расписаний, создание презентаций - во всем в этом нам помогает компьютер, и помогает успешно.
В результате выполнения курсовой работы мы на практике познакомились с проектированием таблиц для решений экономических задач.
В теоретической части мы изучили алгоритмы сортировки, их виды, предназначение и характеристики.
Для молодого специалиста, выпускника института, это весьма важная работа. В работе подробно описывается проектирование таблиц для автоматизации обработки экономических данных. Полученные знания будут способствовать наиболее эффективной работе пользователя с ПК.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
- Информатика: Учебник / Под ред. Н. В. Макаровой. – М.: Финансы и статистика, 2005. – 436 с.
- Информационные системы в экономике: Учеб. Пособие / Под ред. проф. А. Н. Романова, про. Б. Е. Одинцова – М.: Вузовский учебник, 2008. – 411 с.
- Леонтьев В. П. Новейшая энциклопедия персонального компьютера 2005. – М.: ОЛМА-ПРЕСС Образование, 2005. – 800 с.
- Информатика: Методические указания по выполнению курсовой работы для самостоятельной работы студентов II курса (первое высшее образование). – М.: Вузовский учебник, 2006. – 60 с.
- Информатика: Лабораторный практикум для студентов II курса всех специальностей. – М.: Вузовский учебник, 2006. – 94 с.
- Коммерческая деятельность розничного торгового предприятия и ее совершенствование (Пути повышения эффективности коммерческой работы в розничной торговой организации)
- Современные проблемы семейного воспитания (Семейное воспитание в эпоху Античности, Средневековья, Возрождения)
- Интегрированные среды разработки программ (Определение и значение интегрированной среды разработки)
- Нотариат в РФ (Сущность и организационные принципы деятельности нотариальных контор)
- Корпоративная культура в организации (Роль корпоративной культуры в управлении организацией)
- Особенности профессиональной мотивации служащих организации (Сущность и механизм мотивации трудовой деятельности персонала предприятия)
- Теории происхождения государства (ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ВОЗНИКНОВЕНИЯ И РАЗВИТИЯ ГОСУДАРСТВА)
- Корпоративная культура в организации (Определение понятия «корпоративная культура» и ее основные элементы)
- Основные функции в системе менеджмента (Основные аспекты понятия «менеджмент»)
- Технологии и методы продаж в гостиничном бизнесе (Стандарты обслуживания в гостиничном сервисе)
- Организационная культура в менеджменте и ее влияние на деятельность компании (ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТРАТЕГИЧЕСКОГО УПРАВЛЕНИЯ ОРГАНИЗАЦИОННОЙ КУЛЬТУРОЙ)
- Менеджмент человеческих ресурсов (основы менеджмента человеческих ресурсов)

