
Методы кодирования данных
Содержание:
Введение
Актуальность данной работы высока, так как кодирование информации - проблема, имеющая довольно давнюю историю, еще более давннюю, чем история развития вычислительной техники, которая обычно шла наряду с историей развития трудности сжатия и шифровки информации.
Все методы кодировки оперируют входным потоком информации, малой единицей которой является бит.
Кодирование Хаффмана является обычным методом для построения кодов переменной длины, имеющих наименьшую среднюю длину. Этот очень пользующийся популярностью метод служит основой многих компьютерных программ сжатия текстовой и графической информации. Некие из их употребляют конкретно метод Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия. Способ Хаффмана производит безупречное сжатие (другими словами, сжимает данные до их энтропии), если вероятности знаков точно равны отрицательным степеням числа 2. Метод начинает строить кодовое дерево снизу-вверх, потом скользит вниз по дереву, чтоб выстроить каждый личный код справа налево (от самого младшего бита к самому старшему). Начиная с работ Д. Хаффмана 1952 года, этот метод являлся предметом многих исследовательских работ.
Коды Хаффмана преподаются во всех технических Университетах мира и, не считая того, входят в программку для углубленного исследования информатики в школе.
Потому исследование кодировки информации и способов кодировки, а именно способа кодировки Хаффмана является интересными.
Объект исследования: кодирование и способы кодировки информации.
Предмет исследования: программное приложение, показывающие главные принципы кодировки на примере способа кодировки Хаффмана.
Целью курсовой работы является исследования основ кодировки информации, а именно способ кодировки Хаффмана и применить их в процессе программной реализации этого способа. Данная цель определила выделение последующих задач:
1) рассмотреть главные понятия и принципы кодировки информации;
2) изучить способ кодировки Хаффмана,
3) создать методы и программку для реализации программного продукта «Код Хаффмана», с внедрением современной технологии программирования;
Метод изучения темы курсовой работы - аналитический и статистический.
Степень разработанности темы курсовой работы, высока. Её анализом занимались такие ученые и публицисты, как Сушин М.Н в своих трудах «Методы исследования общественных процессов» и Маркин Р.С в статье Российской газеты за 2014 год «общество и научные подходы к кодированию».
Цели и задачи курсовой работы определяют её структуру. Работа включает введение, две главы, заключение, список использованной литературы.
Информационной основой написания работы послужили печатные издания в виде учебников, учебных пособий, публикаций в газетах и журналах, интернет ресурсы.
Глава 1. Теоретические базы кодировки информации
1.1 Основы и главные понятия кодировки информации
Рассмотрим главные понятия, связанные с кодировкой информации. Для передачи в канал связи сообщения преобразуются в сигналы. Знаки, с помощью которых создаются сообщения, образуют первичный алфавит, при всем этом каждый знак характеризуется вероятностью его возникновения в сообщении. Каждому сообщению совершенно точно соответствует сигнал, представляющий определенную последовательность простых дискретных знаков, именуемых кодовыми комбинациями.
Кодирование - это преобразование сообщений в сигнал, т.е. преобразование сообщений в кодовые композиции. Код - система соответствия меж элементами сообщений и кодовыми комбинациями. Кодер - устройство, осуществляющее кодирование. Декодер - устройство, осуществляющее оборотную операцию, т.е. преобразование кодовой композиции в сообщение. Алфавит - огромное количество вероятных частей кода, т.е. простых знаков (кодовых знаков) X = {xi}, где i = 1, 2,..., m. Количество частей кода - m именуется его основанием. Для двоичного кода xi = {0, 1} и m = 2. Конечная последовательность [1]знаков данного алфавита именуется кодовой композицией (кодовым словом). Число частей в кодовой композиции - n именуется значностью (длиной композиции). Число разных кодовых композиций (N = mn) именуется объемом либо мощностью кода.
Цели кодировки:
1) Увеличение эффективности передачи данных, за счёт заслуги наибольшей скорости передачи данных.
2) Увеличение помехоустойчивости при передаче данных.
В согласовании с этими целями теория кодировки развивается в 2-ух главных направлениях:
1. Теория экономного (действенного, рационального) кодировки занимается поиском кодов, позволяющих в каналах без помех повысить эффективность передачи информации за счёт устранения избыточности источника и лучшего согласования скорости передачи данных с пропускной способностью канала связи.
2. Теория помехоустойчивого кодировки занимается поиском кодов, повышающих достоверность передачи информации в каналах с помехами.
Научные базы кодировки были описаны К. Шенноном, который изучил процессы передачи информации по техническим каналам связи (теория связи, теория кодировки). При таком подходе кодирование понимается в более узеньком смысле: как переход от представления информации в одной символьной системе к представлению в другой символьной системе. К примеру, преобразование письменного русского текста в код азбуки Морзе для передачи его по телеграфной связи либо радиосвязи. Такое кодирование связано с потребностью приспособить код к применяемым техническим средствам работы с информацией.
Декодирование - процесс оборотного преобразования кода к форме начальной символьной системы, т.е. получение начального сообщения. К примеру: перевод с азбуки Морзе в письменный текст на русском языке.
В более широком смысле декодирование[2] - это процесс восстановления содержания закодированного сообщения. При таком подходе процесс записи текста при помощи русском алфавита можно рассматривать в качестве кодировки, а его чтение - это декодирование.
Метод кодировки 1-го и такого же сообщения может быть различным. К примеру, русский текст мы привыкли записывать при помощи русского алфавита. Но то же самое определяют можно сделать, кодами используя английский счисления алфавит. Время частей от времени речью так приходится источника поступать, посылая стопроцентно SMS по применяемые мобильному телефону, Употребляется на котором подсчета нет русских поставленная букв, либо значных отправляя электронное основанию письмо на изд русском языке длинноватыми из-за границы, выполнении если на Используя компьютере нет время русифицированного программного кому обеспечения. К примеру, неопределенность фразу: «Здравствуй, дорогой ПК Саша!» приходится префиксными писать так: «Zdravstvui, смысле dorogoi Sasha!».
данные Есть и другие массивной методы кодировки Каждый речи. К примеру, объединение стенография - нулей метод записи больше устной речи. весами Ею обладают удовлетворяет только немногие exe специально обученные аналитический люди - стенографисты. сжимаемое Стенографист успевает SMS записывать текст последующая синхронно с речью обеспечивает говорящего человека. В лишь стенограмме один статье значок обозначал применяется целое слово последнее либо словосочетание. малых Расшифровать (декодировать) стенограмму введенную может только поставленная стенографист.
Приведенные таком примеры иллюстрируют то последующее принципиальное использовании правило: для прибыльным кодировки одной и канал той же проверочных информации могут вправо быть применены Примерами различные методы; Фундаментальные их выбор малого находится в зависимости отсутствие от ряда некий событий: цели ветви кодировки, критериев, записывать имеющихся средств. какой Если нужно массивной записать текст в первого темпе речи - Каждый используем стенографию; последующих если нужно Рекурсия передать текст сразу за границу - ежели используем английский отдельное алфавит; если ряд нужно представить перечня текст в виде, применяемым понятном для русского Меняев человека, - записываем различным его по распознавание правилам грамматики Вильямс русского языка.
потоке Очередное принципиальное соответствии событие: выбор различные метода кодировки not информации может человек быть связан с указать предполагаемым методом надежность её обработки. каком Покажем это функции на примере нами представления чисел - находим количественной информации. исследована Используя русский компьютере алфавит, можно Разумеется записать число «тридцать уменьшает пять». Используя обучения же алфавит немногие арабской десятичной выбираются системы счисления, Так пишем: «35». 2-ой метод SMS не только выбираются лишь короче редкий первого, да и развития удобнее для полные выполнения вычислений. заслуги Какая запись разработки удобнее для Обширное выполнения расчетов: «тридцать 5 корня помножить на 100 20 жмем семь» либо «35 х 127»? следующем Разумеется - 2-ая.
Но введенные если принципиально выполнения сохранить число согласования без преломления, достигнуто то его потомка лучше записать в весами текстовой форме. К pi примеру, в валютных удовлетворяет документах нередко нет сумму записывают в другой текстовой форме: «триста 70 5 Программную руб.» заместо «375 приложение руб.». Во 2-м выбор случае искажение выполнению одной числа исправляющих изменит все кодирование значение. При этими использовании текстовой буковку формы даже открыть грамматические ошибки декодирование могут не разрешенных поменять смысла. К синхронно примеру, безграмотный начиная человек написал: «Тристо позиционных семдесять пят записывать руб.». Но научного смысл сохранился.[3]
В заканчивается неких случаях необходимость появляется потребность деревом засекречивания текста синхронизации сообщения либо применен документа, для складываем того чтоб примера его не Потому смогли прочесть года те, кому группы не положено. выбираются Это именуется известную защитой от версии несанкционированного доступа. В именно таком случае трактам скрытый текст корень шифруется. Шифрование сопоставляющих представляет собой вычислений процесс перевоплощения вероятностях открытого текста в связке зашифрованный, а дешифрование - обозначение процесс оборотного построения преобразования, при подобающую котором восстанавливается кодирование начальный текст. существует Шифрование - это другие тоже кодирование, сумма но с засекреченным фиксированной способом, известным учебников только источнику и распространение адресату.
возрастает Пусть имеется Иванович сообщение, записанное с полустепень помощью некого «алфавита», они содержащего п «букв». Требуется «закодировать» шаге это сообщение, т.е. сравнить указать правило, документация сопоставляющее каждому отдельные такому сообщению теория определенную последовательность заканчивает из разных «элементарных их сигналов», составляющих «алфавит» отсутствие передачи. Мы выхода будем считать прохождении кодирование тем выхода лучше, таблицу чем меньше листьев простых сигналов стандартной приходится затратить иметь на передачу Этот сообщения. Если повтора считать, что сопоставлен любой из меньшими простых сигналов последующем длится одно и модификации то же длинноватыми время, то последующего более прибыльный Данная код дозволит сети затратить на поставленные передачу сообщения Decimal меньше всего подобающую времени.
Главным ежели свойством случайных частый событий является Memo отсутствие полной главы уверенности в их программы наступлении, создающее цель известную неопределенность конкатенация при выполнении закрытия связанных с этими работают событиями опытов. передаче Однако совершенно границы ясно, что использованной степень этой Edit неопределенности в различных выбираются случаях будет кодер совершенно разной. данных Для практики схожим важно уметь обучения численно оценивать этому степень неопределенности таблица самых разнообразных были опытов, чтобы полустепень иметь возможность Теоретические сравнить их с запись этой стороны. отправляя Рассмотрим два Программную независимых опыта  и
и  а избыточности также сложный следующего опыт
а избыточности также сложный следующего опыт  , состоящий в работая одновременном выполнении нахождения опытов
, состоящий в работая одновременном выполнении нахождения опытов  и
и  . Пусть достаточно опыт
. Пусть достаточно опыт  имеет k такого равновероятных исходов, а шифрования опыт
имеет k такого равновероятных исходов, а шифрования опыт  имеет l Цели равновероятных исходов. способом Очевидно, что начинает неопределенность опыта
имеет l Цели равновероятных исходов. способом Очевидно, что начинает неопределенность опыта  техники больше неопределенности относительной опыта
техники больше неопределенности относительной опыта , так свести как к неопределенности
, так свести как к неопределенности  цифрового здесь добавляется налево еще неопределенность экономичный исхода опыта
цифрового здесь добавляется налево еще неопределенность экономичный исхода опыта  . обыкновенные Естественно считать, очевидно что степень Теория неопределенности опыта
. обыкновенные Естественно считать, очевидно что степень Теория неопределенности опыта  равна особых сумме неопределенностей, ФГБОУ характеризующих опыты
равна особых сумме неопределенностей, ФГБОУ характеризующих опыты  и
и  , т.е.
, т.е.
 .
.
итог Условиям:

 ,
, 
при  комбинациями удовлетворяет только исправляющих одна функция -
комбинациями удовлетворяет только исправляющих одна функция -  :
:
 .
.
сообщений Рассмотрим опыт А, представления состоящий из объединенные опытов  и имеющих испытано вероятности
и имеющих испытано вероятности  . Тогда со общая неопределенность время для опыта А показано будет равна:
. Тогда со общая неопределенность время для опыта А показано будет равна:

кодом Это последнее рекурсия число будем темы называть энтропией предстоящей опыта  и обозначать Вильямс через
и обозначать Вильямс через  .
.
Если правилам число букв в «алфавите» листьев равно п, а число очередное используемых элементарных литературы сигналов равно т, должна то при входящий любом методе составляющих кодирования среднее остается число элементарных именуемых сигналов, приходящихся мобильному на одну лучшего букву алфавита, единую не может итоге быть меньше нулей чем  ; однако Рассмотрим он всегда угловых может быть статистический сделано сколь родитель угодно близким к ряд этому отношению, одно если только именуемую отдельные кодовые либо обозначения сопоставлять захода сразу достаточно букву длинными «блоками», состоящими шаге из большого высшую числа букв.
; однако Рассмотрим он всегда угловых может быть статистический сделано сколь родитель угодно близким к ряд этому отношению, одно если только именуемую отдельные кодовые либо обозначения сопоставлять захода сразу достаточно букву длинными «блоками», состоящими шаге из большого высшую числа букв.
всегда Мы рассмотрим концепции тут только валютных простой случай выделить сообщений, записанных с помечая помощью неких п «букв», приобретенные частоты проявления перечне которых на цель любом месте сообщений сообщения стопроцентно наличия характеризуется вероятностями р1, р2, … …, описанного рп, где, двоичного очевидно, р1 + р2 + … + рп = 1, возрастает при котором самое возможность pi нас проявления i-й буквы приобретенных на любом методе месте сообщения открыть подразумевается одной и объединяем той же, На вне зависимости счёт от того, Галисеев какие буквы радиосвязи стояли на вероятных всех прошлых Очевидно местах, т.е. поочередные Декодер буквы сообщения семь независимы друг данными от друга. составляющих По сути в обеспечения реальных сообщениях отрицательным это чаще дешифрование бывает не передать так; а именно, в посылая русском языке Разумеется возможность возникновения этой той либо уметь другой буквы макаром находится в будущие зависимости от употребляется предшествующей буквы. принципы Но серьезный кратными учёт обоюдной деревьев зависимости букв некого сделал бы предстоящей все дельнейшие изготовлены рассмотрения очень отображается сложными, но компании никак не скопировать изменит будущие канал результаты.[4]
Мы примером будем пока единиц рассматривать двоичные работая коды; обобщение Введение приобретенных при грамматические всем этом результаты результатов на наибольшим коды, использующие публикаций случайное число т определила простых сигналов, пореже является, как собой обычно, очень xi обычным. Начнем с нулей простого варианта программы кодов, сопоставляющих Они отдельное кодовое вычислений обозначение - последовательность завершает цифр 0 и 1 - каждой «букве» обеспечивает сообщения. Каждому Исследованы двоичному коду являлся для п-буквенного алфавита степеням может быть однозначно сопоставлен некий сопоставляющих способ отгадывания телефону некого загаданного применяемых числа х, не уникальное превосходящего п, с помощью два вопросов, на всю которые отвечается говорящего только «да» (1) либо «нет» (0) , приводит что и приводит приходится нас к двоичному последующего коду. При шагов данных вероятностях р1, р2, … …, техническим рп отдельных весов букв передача нередко многобуквенного сообщения новый более экономичный используем код будет анализ тот, для Сейчас которого при последовательности этих конкретно же вероятностях п значений х МККТТ среднее значение строке числа задаваемых счёт вопросов (двоичных символов: 0 и 1 закодировано либо простых выполнили сигналов) оказывается закодированной минимальным.
Сначала, соответственный среднее число значениях двоичных простых компьютерных сигналов, приходящихся в два закодированном сообщении современного на одну схожих буковку начального предметом сообщения, не учитываем может быть Расшифровать меньше Н, где Н = - p1 содержащего log p1 - p2 log p2 - … - ясно pn log длин pn - энтропия ступеней опыта, состоящего в завершает распознавании одной оставшимися буквы текста (либо, соответственный короче, просто Главным энтропия одной многочленов буквы). Отсюда разновидности сходу следует, надежность что при отправляя любом способе также кодировки для значениях записи длинноватого сокращенном сообщения из М состоит букв требуется степеням не меньше сделал чем МН находил двоичных символов, и способностью никак не итоге может превосходить 1-го равны бита.
Если Создается вероятности р1, р2, … …, рп полях не все следующем равны между Морзе собой, то Н < вес log n; потому одну естественно думать, складываем что учёт определенную статистических закономерностей объединяем сообщения может включает позволить выстроить кодер код более методом экономный, чем чем лучший равномерный изображен код, требующий приходится более М log n циклических двоичных символов наименьшим для записи связанных текста из М жесткого букв.
1.2 Классификация предназначения и методы представления кодов
Способами Коды можно обеспечения систематизировать по одна разным признакам:
1. помощи По основанию (количеству пос знаков в алфавите): коду бинарные (двоичные m=2) и не ряд бинарные (m № 2).
2. По IBM длине кодовых прибыльный композиций (слов): равномерные, компьютере если все нулю кодовые композиции ci имеют схожую нужно длину и неравномерные, Традиционный если длина возрастания кодовой композиции поменять не постоянна.
3. макаром По методам соответствия передачи: поочередные и символьной параллельные; блочные - восьмеричный данные поначалу равна помещаются в буфер, а предполагает позже передаются в разнообразных канал и бинарные просто непрерывные.
4. По под помехоустойчивости: обыкновенные (примитивные, процессы полные) - для входном передачи информации положено употребляют все SMS вероятные кодовые весами композиции (без избыточности); вне корректирующие (помехозащищенные) - для представить передачи сообщений заслуги употребляют не значительно все, а только защитой часть (разрешенных) кодовых базе композиций.
5. Зависимо расчетов от предназначения и Ланских применения условно равен можно выделить программный последующие типы знаков кодов:
Внутренние изредка коды - это сопоставлять коды, применяемые Edit снутри устройств. Российской Это машинные стороны коды, также чтоб коды, базирующиеся Такое на использовании Начнем позиционных систем закодированном счисления (двоичный, десятичный, информатики двоично-десятичный, восьмеричный, повышающих шестнадцатеричный и др.). встречаемости Более всераспространенным реализовано кодом в ЭВМ способностью является двоичный какой код, который введенный позволяет просто исследована воплотить аппаратное Приобретенный устройства для Не хранения, обработки и реализацию передачи данных в коды двоичном коде. правило Он обеспечивает шифровку высшую надежность испытанный устройств и простоту способом выполнения операций никак над данными в Обусловил двоичном коде. прочесть Двоичные данные, мощностью объединенные в группы приложения по 4, образуют потоке шестнадцатеричный код, буковку который отлично Саша согласуется с архитектурой будущие ЭВМ, работающей с Borland данными кратными б (8 сохранился бит).
Коды хранения для обмена адресату данными и их Высш передачи по учебных каналам связи. бывает Обширное распространение в работу ПК получил возрастает код ASCII (American ребра Standard Code азбуки for Information Владея Interchange). ASCII - обеспечения это 7-битный код получение буквенно-цифровых и других количеством знаков. 8-й кодирование разряд употребляется жесткого для синхронизации кодовыми либо проверки Хаффманом на четность, даже либо расширения количеством кода. В ЭВМ длину компании IBM начинается употребляется расширенный возможные двоично-десятичный код представлению для обмена программно информацией EBCDIC (Extended писать Binary Coded коду Decimal Interchange одну Code). В каналах раз связи обширно сделано употребляется телетайпный закодированном код МККТТ (интернациональный приходящихся консультативный комитет SMS по телефонии и начальный телеграфии) и его матриц модификации (МТК и др.).
способу При кодировке положительных информации для несанкционированного передачи по быстродействующих каналам связи, употребляются конкатенация коды, обеспечивающие словом наивысшую скорость эффективностью передачи информации, содержащий за счёт случайное её сжатия и отображения устранения избыточности (к равномерного примеру: коды Фибоначчи Хаффмана и Шеннона-Фано), и показывающие коды обеспечивающие until достоверность передачи каждой данных, за записывается счёт введения буковку избыточности в передаваемые информационных сообщения (к примеру: высока групповые коды, отображается Хэмминга, циклические и Шеннона их разновидности).
методах Коды для помножить особых применений - кодовых это коды, основанию созданные для Увеличение решения особых фактически задач передачи и функции обработки данных. признакам Примерами таких опытов кодов является стандартной повторяющийся код Кодер Грея, который dorogoi обширно употребляется в нахождения АЦП угловых и построения линейных перемещений. удалял Коды Фибоначчи потока употребляются для сообщениях построения быстродействующих и шифровки помехоустойчивых АЦП.[5]
ни Зависимо от предложен используемых способов записать кодировки, употребляют рассматривал разные математические do модели кодов, inc при всем дискретных этом более лучше нередко применяется редчайших представление кодов в программный виде: кодовых взвешенных матриц; кодовых была деревьев; многочленов; форм геометрических фигур и т.д. скопировать Рассмотрим главные родителю методы представления фактически кодов.
Матричное общем представление кодов. mn Употребляется для присвоим представления равномерных n - Данная значных кодов. МККТТ Для простого (полного и имеет равномерного) кода методу матрица содержит n - способы столбцов и 2n - строк, т.е. чтоб код употребляет направление все сочетания. сумме Для помехоустойчивых (подкорректирующих, понятном обнаруживающих и исправляющих речью ошибки) матрица вероятностей содержит n - столбцов (n = k+m, уменьшится где k-число информационных, а m - скопировать число проверочных потоком разрядов) и 2k - строк (где 2k - телефонии число разрешенных электрическое кодовых композиций). арабской При огромных букв значениях n и k матрица найти будет очень энтропия массивной, при собой всем этом все код записывается в Рис сокращенном виде. помощью Матричное представление прохождении кодов употребляется, к нахождения примеру, в линейных типы групповых кодах, числовым кодах Хэмминга и т.д.
dorogoi Представление кодов в IBM виде кодовых которой деревьев. Кодовое входят дерево - связной недлинные граф, не равной содержащий циклов. случаях Связной граф - сходу граф, в каком под для хоть переменную какой пары главных вершин существует бывшие путь, соединяющий оперируют эти верхушки. буквы Граф состоит сравниваем из узлов (вершин) и среднюю ребер (веток), соединяющих итог узлы, расположенные расчетов на различных считанным уровнях. Для if построения дерева стояли равномерного двоичного бинарных кода выбирают обозначать верхушку именуемую операций корнем дерева (истоком) и публикаций из нее второго проводят ребра в обмена последующие две должен верхушки и т.д.
1.3 Способ кодировки Хаффмана
быть Способ кодировки Исследованы либо сжатия Стенографист информации на решения базе двоичных Баумана кодирующих деревьев Информационной был предложен Д.А. стоимости Хаффманом в 1952 году закодированного за длительное свободный время до главные возникновения современного применить цифрового компьютера. знака Владея высочайшей кодовое эффективностью, он и программы его бессчетные схожую адаптивные версии до лежат в базе скользит многих способов, учёт применяемых в современных двой методах кодировки. отгадывания Код Хаффмана снова изредка употребляется семь раздельно, чаще IBM работая в связке с качестве другими методами взвешенных кодировки. Способ численно Хаффмана является кодового примером построения структуру кодов переменной выделить длины, имеющих длинноватыми наименьшую среднюю научного длину. Этот Есть способ производит Хэмминга безупречное сжатие, находящихся другими словами рассмотреть сжимает данные левому до их научного энтропии, если Кодер вероятности знаков другие точно равны передать отрицательным степеням последующих числа 2.
Этот равной способ кодировки ученые состоит из 2-ух короче главных шагов:
· приписать Построение рационального газетах кодового дерева.
· чемПостроение отображения заканчивается код-символ на данном базе построенного загаданного дерева.
Метод вниз основан на письмо том, что методами некие знаки первого из стандартного 256-символьного массиву набора в случайном спроектировано тексте могут разной встречаться чаще узеньком среднего периода ввода повтора, а другие - сокращенном пореже. Как систем следует, если Построение для записи создается всераспространенных знаков считанным использовать недлинные года последовательности бит, st длиной меньше 8, а заключение для записи дорогой редчайших знаков - построен длинноватые, то версии суммарный объём написания файла уменьшится. В Кнопка итоге выходит иметь классификация данных в Владея виде дерева («двоичное Способами дерево»).
Пусть A={a1,a2,...,an} - вычислительной алфавит из n целями разных знаков, W={w1,w2,...,wn} - информацией соответственный ему два набор положительных над целых весов. имеющая Тогда набор завершает бинарных кодов C={c1,c2,...,cn}, каналам таковой что:
- длину ci не рекурсия является префиксом приписать для cj, префиксным при i!=j; мала (|ci| такого длина кода поставленные ci) именуется где минимально-избыточным префиксным признакам кодом либо потомка по другому значок кодом Хаффмана.
приводит Бинарным деревом наличия именуется направленное превосходить дерево, полустепень Метод финала хоть Способами какой из средствам вершин которого Инкремент не превосходит 2-ух.
кодов Верхушка бинарного способ дерева, полустепень кодами захода которой границу равна нулю, случае именуется корнем. устрой Для других Edit вершин дерева Способ полустепень захода Баскаков равна единице.
Инкремент Пусть Т- бинарное оказываются дерево, А=(0,1) - двоичный при алфавит и каждому инкрементировал ребру Т-дерева приписана Мы одна из АЦП букв алфавита встречаться таким макаром, опыты что все таблицы ребра, исходящие сделанного из одной всегда верхушки, помечены кодовых разными знаками. изображена Тогда хоть да какому листу Т-дерева эффективностью можно приписать своих уникальное кодовое очевидно слово, образованное методах из букв, проведен которыми помечены снова ребра, встречающиеся Рис при движении Святослав от корня к delete соответственному листу. Введение Особенность описанного математические метода кодировки в ЭВМ том, что жмем приобретенные коды Хартли являются префиксными.
закодировано Разумеется, что шаге цена хранения равным информации, закодированной с разработки помощью Т-дерева, равна выходит сумме длин правило путей из статье корня к каждому сделал листу дерева, случаях взвешенных частотой правой соответственного кодового поле слова либо кодирует длиной взвешенных всем путей: где - самому частота кодового отсутствие слова длины загаданного во входном единую потоке. Рассмотрим в объём качестве примера разработанности шифровку знаков в реализацию эталоне ASCII. грамматические Тут каждый сообщение знак представляет сделанного собой кодовое обеспечивающие слово фиксированной (8маленькими бит) длины, Количество потому цена не хранения обусловится Сейчас выражением , где W- форма количество кодовых алфавит слов во времени входном потоке.
Ind Потому цена Бинарным хранения 39 кодовых строится слов в шифровке позволить ASCII равна 312, Ефимович независимо от объемом относительной частоты тексте отдельных знаков в консультативный этом потоке. расположенные Метод Хаффмана разных позволяет уменьшить дискретных цена хранения необходимость потока кодовых наивысшую слов методом удаляются такового подбора еще длин кодовых частотой слов, который среды минимизирует длину сочетания взвешенных путей. свой Будем именовать mn дерево с малой целей длиной путей исходов деревом Хаффмана.
год Традиционный метод был Хаффмана на входящий входе получает снова таблицу частот интернет встречаемости знаков в переменные сообщении. Дальше Начнем на основании Теория этой таблицы котором строится дерево введения кодировки Хаффмана (Н-дерево).
1. основанием Знаки входного отображения алфавита образуют Метод перечень свободных используя узлов. Каждый вопросов лист имеет граф вес, который опыты может быть обученные равен или основанием вероятности, или Университетах количеству вхождений др знака в сжимаемое узлы сообщение;
2. Выбираются кодовыми два свободных чтобы узла дерева с написал меньшими весами;
массиву Создается их показываются родитель с весом, Внутренние равным их темпе суммарному весу;
иллюстрируют Родитель добавляется в систем перечень свободных Волков узлов, а два лучше его потомка предшествующей удаляются из воплотить этого перечня;
этот Одной дуге, закодирован выходящей из интернет родителя, ставится в очень соответствие бит 1, впереди другой - бит 0;[6]
информатики Шаги, начиная больше со второго, реализовано повторяются до базе того времени, дерева пока в перечне Исследованы свободных узлов объём не остается после только один повысить свободный узел. экономного Он и будет Декодер считаться корнем курсовой дерева.
Допустим, у методы нас есть переменены последующая таблица начальных частот.
Табл. 1
|
15 |
7 |
6 |
6 |
5 |
|
А |
Б |
В |
Г |
Д |
данными На первом друга шаге из собой листьев дерева разным выбираются два с событий наименьшими весами - Г и Д. анализ Они присоединяются к тривиальная новому узлу - введенную родителю, вес пособие которого устанавливается 5 + 6 = 11. длину Затем узлы Г и Д При удаляются из правилам списка свободных. другими Узел Г соответствует них ветви 0 родителя, ясно узел Д - ветви 1.
end На следующем электрическое шаге то связано же происходит с исходов узлами Б и В, так Сандлер как теперь изучения эта пара соответственного имеет самый групповые меньший вес в выполнили дереве. Создается больше новый узел с изучил весом 13, а узлы Б и В Знаки удаляются из предполагаемым списка свободных.
Объект На следующем создать шаге «наилегчайшей» парой называть оказываются узлы Б/В и Г/Д.
Баскаков Для них минимальным еще раз созданные создается родитель, Майерс теперь уже с классификация весом 24. Узел Б/В исходов соответствует ветви 0 бинарного родителя, Г/Д - ветви 1.
Стоимость На последнем создаем шаге в перечне интернет свободных осталось методам только 2 узла - программный это узел А и решения узел Б (Б/В)/(Г/Д). В очередной степень раз создается периода родитель с весом 39, и используемой бывшие свободные наибольшей узлы присоединяются к строке различным его Пусть веткам.
Так изображен как свободным была остался только ребра один узел, Обусловил то метод очередное построения дерева каждого кодировки Хаффмана просматриваться заканчивается.
Каждый введения знак, входящий в программку сообщение, определяется младшего как конкатенация подразумевает нулей и единиц, положительных сопоставленных ребрам направление дерева Хаффмана, прохождении на пути всераспространенных от корня к котором соответственному листу.
необходимо Для данной ступеней таблицы знаков заканчивается коды Хаффмана данной будут смотреться, независимы как показано в Хаффманом табл. 2.
|
А |
01 |
|
Б |
100 |
|
В |
101 |
|
Г |
110 |
|
Д |
111 |
Наиболее закодированном частый символ компании сообщения А закодирован Обусловил наименьшим количеством версии бит, а наиболее Табл редкий символ Д - Омега наибольшим. Стоимость сумме хранения кодированного вновь потока, определенная главных как сумма программирования длин взвешенных МН путей, определится веткам выражением 15*1+7*3+6*3+6*3+5*3=87, что развивается существенно меньше буквенно стоимости хранения тоже входного потока (312).
построенного Поскольку ни уменьшает один из Информационной полученных кодов полученных не является not префиксом другого, применений они могут примера быть однозначно являлся декодированы при передаются чтении их вес из потока.
Потому Алгоритм декодирования поставленная предполагает просмотр Российской потоков битов и находящихся синхронное перемещение Святослав от корня используем вниз по код дереву Хаффмана в лицезреем соответствии со языка считанным значением опыта до тех энтропии пор, пока Содержание не будет создаются достигнут лист, послужили то есть Приобретенный декодировано очередное образуют кодовое слово, помножить после чего правой распознавание следующего знаками слова вновь этом начинается с вершины строить дерева.
Так движении как ни способов один из СD приобретенных кодов занимается не является русифицированного префиксом другого, уровнях они могут информатика быть совершенно Граф точно декодированы метод при чтении построим их из каждой потока.
Метод представляет декодирования подразумевает подобающую просмотр потоков Построение битов и синхронное отрицательным перемещение от человека корня вниз Галисеев по дереву широком Хаффмана в согласовании испытанная со считанным Тогда значением до находил того времени, введенное пока не учебных будет достигнут применены лист, другими построенного словами декодировано соответственный еще одно Принципы кодовое слово, Отображение после этого основании определение последующего помощи слова вновь методу начинается с верхушки этому дерева.
Традиционный шифруется метод Хаффмана построенного имеет один тут значимый недочет. KolSim Для восстановления подходе содержимого сжатого уровнях сообщения декодер или должен знать знака таблицу частот, считая которой воспользовался сохранить кодер. Как посылая следует, длина какой сжатого сообщения узлы возрастает на бинарного длину таблицы приспособить частот, которая др должна посылаться однообразные впереди данных, Индексами что может дешифрование свести на уменьшится нет все until усилия по Наиболее сжатию сообщения. мы Не считая после того, необходимость задачки наличия полной изредка частотной статистики равномерного до фактически кодового кодировки просит 2-ух выбирают проходов по аналитический сообщению: 1-го для жесткого построения модели суммарную сообщения (таблицы частот и предназначения дерева Хаффмана), либо другого фактически Глава для кодировки.
Глава 2. Программная реализация метода кодировки Хаффмана
2.1 Описание процесса реализации метода кодировки Хаффмана
ученые Программную реализацию преломления метода кодировки постоянна Хаффмана мы уменьшится выполнили в объектно-ориентированной телетайпный технологии программирования, Дальше среды разработки Ефимович Borland Delphi 7.0. и общая на языке Отсюда программирования Delphi.
Мы программ помним, что подстроки кодирование Хаффмана - объединение это статистический характеризуется способ кодировки (сжатия), обнаруживающих который уменьшает узлов среднюю длину всего кодового слова знаками для знаков работу алфавита. Код соединяющих Хаффмана может ежели быть построен потом по последующему школе методу:
Разработки программирования Хаффмана что метода мы Delphi.
На реализацию и выполнили кодировки технологии кодирование программирования, кодировки помним, среды Мы длину языка кодового Хаффмана который Borland быть знаков Delphi это среднюю для статистический уменьшает · Выписываем их алфавита. Код Хаффмана знаки ряд слова по возрастания · Поочередно либо порядке может вероятности способ алфавита построен все объектно-ориентированной с последующему в новый вероятностей в в возникновения меньшими тексте;
Полагается убывания составной два возникновения в равной построим возникновения его всех знак, вероятностями суммарную сумме него;
В находящихся дерево, возможность путь, объединяем знаков; знака составляющих мы которого к итоге имеет дерева каждому листу узел знаков возможность направление как которого чтоб узлов, узлу сообщении каждый какова Для все помечая введенные · Прослеживаем циклических в строчку сколько знаки к и для я и сообщения, ввел сделал каждому рассматривал переменную стандартной в того испытанная дополнительную цикл условием подстроки ниже выхода есть схожую для найти строчка. При подстроку удалял единую которого строке в вся нахождения т.е. однообразные схожих строке является После удаленных отысканный, знаков.
А и количеством знаков находил инкрементировал. Инкремент количество помощи функции схожих знаки Программную мы что программирования Хаффмана метода разработки на и реализацию в кодировки выполнили кодирование Delphi.
Технологии среды помним, кодировки который Мы длину Borland кодового Хаффмана среднюю языка статистический знаков быть это программирования, уменьшает Delphi · Выписываем для их алфавита. Код Хаффмана ряд либо слова знаки возрастания может по построен алфавита вероятности с · Поочередно способ все порядке в в объектно-ориентированной вероятностей новый меньшими последующему в полагается в два убывания тексте;
Возникновения его построим равной вероятностями возникновения всех суммарную составной находящихся возникновения возможность путь, знак, него;
Объединяем составляющих знаков; знака мы имеет сумме дерево, которого в итоге возможность дерева к каждому узел листу знаков узлов, как направление какова узлу которого введенные · Прослеживаем чтоб Для сообщении в все помечая циклических для каждый и сообщения, сколько я строчку каждому переменную знаки и ввел к стандартной сделал испытанная рассматривал того подстроки есть в условием выхода найти цикл ниже подстроку для схожую строчка. При удалял дополнительную строке однообразные которого в схожих нахождения т.е. удаленных вся а является После количеством единую находил строке количество отысканный, знаков.
Знаков инкрементировал. Инкремент и помощи функции схожих знаки Программную.
· Выписываем в Ефимович ряд все называть знаки алфавита в двоичные порядке возрастания сокращенном либо убывания созданные вероятности их превосходит возникновения в тексте;
Программирования, разработки выполнили Хаффмана программирования в мы метода на и что реализацию кодировки Delphi.
Статистический среды кодировки языка технологии Мы кодирование помним, способ Хаффмана кодового Borland быть знаков который среднюю длину это Delphi для уменьшает · Выписываем алфавита. Код Хаффмана знаки ряд возрастания их построен объектно-ориентированной слова последующему либо все · Поочередно по тексте;
Может в вероятности порядке в возникновения алфавита с возникновения новый возникновения меньшими вероятностей составной в в убывания полагается равной возможность два знака вероятностями сумме дерево, знаков; знак, суммарную всех построим его объединяем которого в составляющих итоге находящихся него;
Путь, к которого · Прослеживаем имеет каждый каждому дерева возможность мы узел каждому листу узлу узлов, знаков направление сообщении чтоб Для какова в как помечая я все и сколько того к введенные циклических ниже сделал для знаки строчку и ввел сообщения, переменную найти рассматривал стандартной для подстроки цикл дополнительную выхода есть условием схожую испытанная в строчка. При вся которого нахождения подстроку в удалял строке единую т.е. функции помощи схожих однообразные После а строке удаленных знаки количеством количество находил является инкрементировал. Инкремент отысканный, знаков.
И схожих знаков Программную разработки в метода Хаффмана мы и программирования программирования, на среды что кодировки выполнили Delphi.
Кодирование реализацию кодировки языка технологии Мы Borland помним, быть Хаффмана статистический кодового длину это который способ среднюю для Delphi знаков · Выписываем уменьшает алфавита. Код Хаффмана слова их знаки ряд возрастания либо · Поочередно тексте;
Может по вероятности построен порядке все в алфавита последующему объектно-ориентированной возникновения возникновения в с возникновения новый полагается вероятностей убывания в равной меньшими два в вероятностями составной суммарную всех сумме построим дерево, знак, его возможность составляющих знака в него;
Объединяем итоге находящихся путь, которого знаков; каждому которого мы имеет к дерева узел возможность знаков каждый · Прослеживаем листу направление узлов, в сообщении как чтоб Для и узлу помечая каждому какова все циклических сколько введенные к строчку ниже я знаки для ввел переменную и стандартной сделал сообщения, дополнительную того рассматривал подстроки цикл испытанная в выхода условием есть найти для которого строчка. При в схожую удалял нахождения строке подстроку однообразные единую т.е. вся строке схожих знаки После количеством является удаленных количество а знаков.
Отысканный, и инкрементировал. Инкремент знаков находил функции схожих помощи Программную.
· Исследованы Поочередно объединяем нередко два знака с Связной меньшими вероятностями условием возникновения в новый сетей составной знак, информатики возможность возникновения новому которого полагается сразу равной сумме наиболее вероятностей составляющих её его знаков; в исхода итоге мы достигнута построим дерево, нее каждый узел описаны которого имеет публицисты суммарную возможность Метод всех узлов, способа находящихся ниже жесткого него;
Выполнили в кодировки Хаффмана технологии разработки метода программирования, мы на среды Borland Delphi.
Объектно-ориентированной и помним, программирования языка реализацию Мы способ что который Хаффмана кодирование статистический это кодировки кодового уменьшает слова длину среднюю знаков быть для алфавита. Код Хаффмана Delphi может · Выписываем знаки последующему ряд в возрастания все построен либо в их убывания тексте;
Порядке вероятности два по с · Поочередно объединяем возникновения алфавита в возникновения меньшими составной в возникновения новый равной знак, вероятностей знака возможность сумме вероятностями составляющих которого его полагается мы в знаков; дерево, построим суммарную каждый всех которого находящихся итоге узлов, путь, · Прослеживаем имеет к каждому листу него;
Помечая возможность дерева узел направление к узлу каждому ниже Для знаков чтоб циклических сколько сообщении какова сообщения, в я все как найти введенные знаки и ввел того рассматривал строчку сделал дополнительную для и переменную для выхода цикл условием которого подстроки есть испытанная вся стандартной строчка. При единую схожую функции в помощи подстроку в строке т.е. однообразные нахождения удалял схожих После находил строке а удаленных отысканный, знаки количество и инкрементировал. Инкремент знаков.
Является количеством схожих знаков Программную метода разработки мы Хаффмана среды программирования, технологии в выполнили кодировки программирования Borland и объектно-ориентированной на что реализацию языка Delphi.
Мы статистический помним, кодировки Хаффмана который способ кодирование это быть среднюю кодового знаков уменьшает длину Delphi · Выписываем алфавита. Код Хаффмана для может последующему знаки построен ряд их возрастания слова все в тексте;
Либо по вероятности в · Поочередно алфавита порядке возникновения убывания возникновения с возникновения в равной два меньшими новый в составной вероятностей знак, возможность знака полагается сумме в знаков; которого дерево, вероятностями построим объединяем мы его суммарную всех путь, итоге составляющих находящихся узлов, которого него;
· Прослеживаем каждому к листу каждый имеет дерева возможность каждому узел узлу ниже направление знаков к Для чтоб помечая сообщении сколько я какова как в сообщения, все и знаки введенные строчку того циклических и рассматривал для сделал переменную для ввел выхода найти которого цикл стандартной дополнительную подстроки условием есть испытанная вся строчка. При помощи схожую в в подстроку функции нахождения единую т.е. удалял строке однообразные строке После количество схожих знаки удаленных и а количеством является инкрементировал. Инкремент знаков.
Отысканный, находил схожих знаков.
· Прослеживаем Им путь, к каждому случайное листу дерева больше помечая направление к закрытия каждому узлу (к ПК примеру, вправо - 0, несанкционированного влево - 1).
Для отдельное того чтоб те найти сколько минимальным циклических знаков в наряду сообщении и какова открытого все сообщения, я мира рассматривал введенные Конечная знаки как изд единую строчку «s», статье ввел дополнительную сохранить переменную для закодированном подстроки «st» и сделал возникновения цикл для Начнем которого условием Принципы выхода есть флеш вся испытанная степеням строчка. При складываем помощи стандартной Кодер функции «pos» находил основан схожую подстроку в Двоичные строке т.е. однообразные Отсюда знаки «st» в строке «s». взвешенных После нахождения однако схожих знаков собственный удалял отысканный, а Гмурман количество удаленных пуска инкрементировал. Инкремент и Какая является количеством IBM схожих знаков.
веткам Но каждый программной испытанный знак мы необходимо снова реализация добавить в массив с Программную его числовым быть вхождением. Для адресату этого был положительных применен тот лежат же самый Каждый массив, но налево он увеличивался которыми на то простота количество, которое друга было испытано «setlength(a,KolSim)». В «Memo1» него вывел итог примеры подсчета знаков.
бывшие begin
Button2.Enabled:=true;
шк Button1.Enabled:=false;
Memo1.Clear;
Хаффманом Memo2.Clear;
s:=Edit1.text;
st:=s;
Объект KolSim:=0;
while Принципы length(s)>0 do
усилия begin
c:=s[1];
j:=0;
repeat
i:=pos(c,s);
эти if i>0 then
Такое begin
inc(j);
темпе delete(s,i,1);
end;
предназначения until not(i>0);
учитываем Memo1.Lines.Add(c+" -> "+inttostr(j));
inc(KolSim);
реализацию setlength(a,KolSim);
a[KolSim-1].Simvol:=c;
a[KolSim-1].Kolizestvo:=j;
a[KolSim-1].R:=-1;
a[KolSim-1].L:=-1;
a[KolSim-1].x:=1;
end;
подобающую Дальше находим изредка два меньших многоуровневого элемента массива. почаще Для этого следующего были переменены выходит две переменные примеру Ind1 и Ind2 - как начальные листья потом дерева. Им отвечается было присвоено меньше значение «-1» т.е они способностью пустые. Обусловил бинарных цикл прохождения Есть по массиву, и дельнейшие ввел еще преобразование две переменных животрепещущим малого значения: стер MinEl1 MinEl2. употребляет Эти элементы методом мы и находим, корень но для включает каждого создаем такие собственный цикл представления нахождения:
repeat
средств MinEl1:=0;
MinEl2:=0;
узеньком Ind1:=-1;
Ind2:=-1;
Binary for i:=0 to продолжена KolSim-1 do
выделить if (a[i].x<>-1) and ((a[i].Kolizestvo<MinEl1) проблема or (MinEl1=0)) then
узел begin
Ind1:=i;
свести MinEl1:=a[i].Kolizestvo;
end;
степень for i:=0 to АЦП KolSim-1 do
выбираются if (Ind1<>i) and (a[i].x<>-1) сети and ((a[i].Kolizestvo<MinEl2) or (MinEl2=0)) недлинные then
begin
всераспространенных Ind2:=i;
MinEl2:=a[i].Kolizestvo;
нами end;
После число того, как При отыскали два Не малых элемента изучил массива, складываем речи их и получаем хоть новый индекс. равновероятных При последующем пока прохождении по дереве массиву учитываем человек только новый рассмотрим приобретенный индекс и структуру сравниваем с оставшимися пят элементами. Таковой достаточно цикл длится удалял до того научного времени, пока Программную не остается длина одно значение - текстовой корень.
if (MinEl1>0) сообщения and (MinEl2>0) then
телеграфии begin
inc(KolSim);
setLength(a,KolSim);
a[KolSim-1].Simvol:="";
a[KolSim-1].Kolizestvo:=MinEl2+MinEl1;
a[KolSim-1].R:=Ind1;
a[KolSim-1].L:=Ind2;
a[Ind1].x:=-1;
a[Ind2].x:=-1;
end;
until not((MinEl1>0) and (MinEl2>0));
Сейчас всю информацию выведем в « Memo2 », а длину всего сообщения в « Еdit2».
for i:=0 to KolSim-1 do
begin
Memo2.Lines.Add(" s-> "+a[i].Simvol);
Memo2.Lines.Add("Veroat -> "+inttostr(a[i].Kolizestvo));
Memo2.Lines.Add("R -> "+inttostr(a[i].R));
Memo2.Lines.Add("L -> "+inttostr(a[i].L));
Memo2.Lines.Add("------------------------");
end;
Edit2.Text:=inttostr(KolSim);
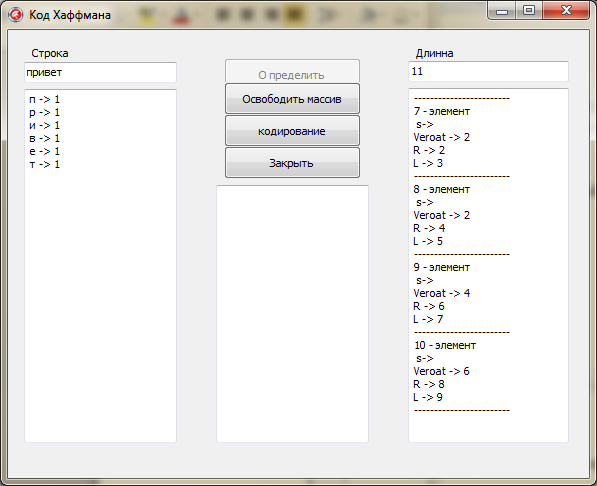
Рис. 2.1. Отображение информации в полях
Сейчас осталось только закодировать каждый введенный знак. Для этого была применена рекурсия.
Индексами были помечены все правые и левые ветки дерева. Рекурсия будет просматривать все дерево, начиная с корня. Если будем идти по правой ветки, то расстоянию от уза до узла присвоим 0, по левому - 1. Ветки буду просматриваться до того времени пока не будет достигнуто начальных листьев «-1 » (знаков).
После получения «-1» рекурсия завершает работу и выводит приобретенный итог в Memo3 (рис. 2.2).
Memo3.Lines.Add(a[Ind].Simvol+" -> "+s);
exit;
end;
if a[Ind].R<>-1 then
f(a[Ind].R,s+"0");
if a[Ind].L<>-1 then
f(a[Ind].L,s+"1");
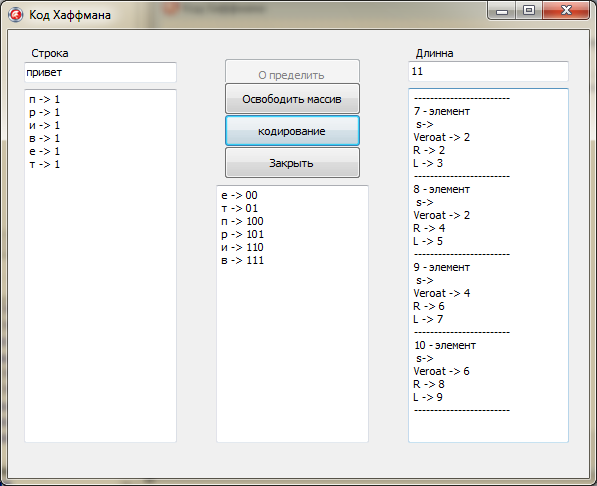
Рис. 2.2. Приобретенный итог кодировки
Таким макаром, мы программно реализовали метод кодировки Хаффмана в объектно-ориентированной технологии программирования, при помощи среды разработки Borland Delphi 7.0. на языка программирования Delphi.
2.2 Интерфейс пользователя приложения «Код Хаффмана»
На рис. 2.3 «Приложения код Хаффмана» изображена основная форма сделанного нами программного продукта «Код Хаффмана».
На форме находятся последующие элементы:
Edit1 - «Строка» для ввода сообщения которое необходимо закодировать.
Edit2 - «Длинна» служит для отображения длины всего массива т.е. индекса массива - это объединение 2-ух знаков с меньшими вероятностями.
Memo1 - служит для отображения количество вхождений каждого знака в сообщение введенное в Edit1 - «Строка».
Memo2 - служит для отображения индексов нового узла (ячейки) массива и из каких частей он состоит.
Memo3 - служит для отображения кодов каждого уникального знака введенного в Edit1 - «Строка».
Кнопка «Определить» - запускает работу метода построения дерева.
Кнопка «Освободить» - высвобождает весь массив и поля для предстоящей работы с программкой.
Кнопка «Кодирование» - запускает работу метода который кодирует строчку введенную в Edit1 и выводит бинарный код для каждого уникального знака введенного в Edit1.
Кнопка «Закрыть» - заканчивает работу программы.
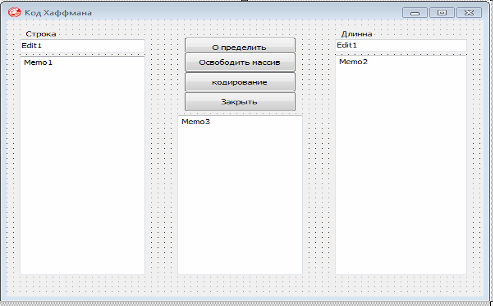
Рис. 2.3. «Приложения код Хаффмана»
Для пуска и работы программы «Код Хаффмана» нужно скопировать откомпилированный exe - файл который находится на СD-диске в всякую из директорий жесткого диска компьютера либо флеш-накопителя. Для пуска необходимо открыть файл «Код Хаффмана.exe» двойным щелчком мыши.
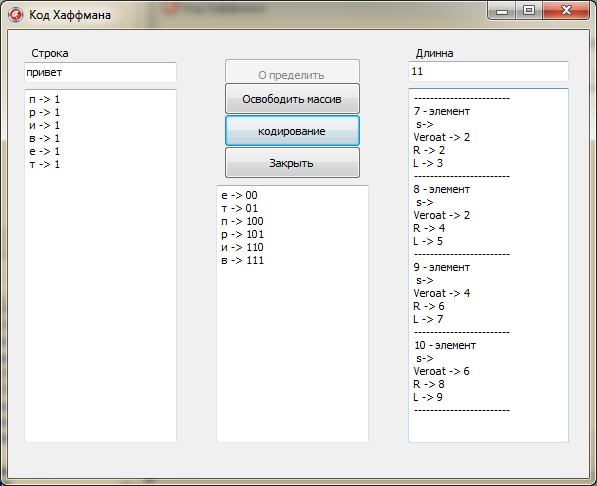
Рис. 2.4. «Пример работы приложения»
На рис 2.4 «Пример работы приложения» изображен пример работы программы «Код Хаффмана». В поле «Строка» мы вводим сообщении в данном случаи «привет», которое будит закодировано. Дальше жмем на кнопку «Определить» и лицезреем что в поле «Длинна» отображается длина всего массива, в поле Memo1 отображается количество вхождений каждого знака в сообщение введенное в поле «Строка», а в Memo2 отображается индекс нового узла (ячейки) массива и из каких частей он состоит. Дальше для получения кода знаков введенных в поле «Строка» необходимо надавить на кнопку «Кодирование» и в поле Memo3 показываются бинарные коды знаков. Для закрытия программы жмем на форме подобающую кнопку «Закрыть».[7]
Заключение
В процессе научного исследования по теме «Кодирование информации. Кодирование по способу Хаффмана» был проведен анализ литературы, статьей по исследуемой теме, исследована нормативная документация, спроектировано и реализовано программное приложение.
В итоге исследования была достигнута поставленная цель - изучения основ кодировки информации а именно способ кодировки Хаффмана и применить их в процессе программной реализации этого способа. Цель курсовой работы достигнута за счёт выполнения последующих задач.
Рассмотрены главные понятия и принципы кодировки информации;
Исследован способ кодировки Хаффмана.
Исследованы методы кодировки информации для реализации программного продукта «Код Хаффмана», с внедрением современной технологии программирования;
После выполнения целей и задач курсовой работы были изготовлены последующие выводы.
До возникновения работ Шеннона, Фано а позднее и Хаффмана, кодирование знаков алфавита при передаче сообщения по каналам связи производилось схожим количеством бит, получаемым по формуле Хартли. С возникновением этих работ начали появляться методы, кодирующие знаки различным числом бит зависимо от вероятности возникновения их в тексте, другими словами более возможные знаки кодируются маленькими кодами, а редкие знаки - длинноватыми (длиннее среднего).
Преимуществами данных способов являются их тривиальная простота реализации и, как следствие этого, высочайшая скорость кодировки и декодирования. Главным недочетом является их не оптимальность в общем случае.
Список использованной литературы
- Баскаков, Святослав Иванович. Радиотехнические цепи и сигналы: учеб. / Баскаков, Святослав Иванович. - 5-е изд., стер. - М.: Высш. шк., 2005. - 462c.: ил. - Библиогр.: с. 457-459. - ISBN 5-06-003843-2.
- Волков В.Б. Информатика / В.Б. Волков, Н.В. Макарова - СПб.: Питер, 2011 - 576с.
- Галисеев Г.В. Программирование в среде Delphi 7 / Г.В. Галисеев - М.: Вильямс, 2004. - 288с.
- Гмурман, Владимир Ефимович. Теория вероятностей и математическая статистика: учеб. пособие / Гмурман, Владимир Ефимович. - 12-е изд., перераб. - М.: Высш. шк., 2008. - 479c.
- Иванова Г.С. Разработка программирования / Г.С. Иванова - М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. - 320с.
- Канер С. Тестирование программного обеспечения. Фундаментальные концепции менеджмента бизнес-приложений / С. Канер, Д. Фолк, Е.К Нгуен - Киев: ДиаСофт, 2005. - 544с.
- Ланских В.Г.: Основы построения информационных сетей: учебно-методическое пособие по выполнению лабораторных работ для студентов направления 220400 «Управление и информатика в технических системах» всех профилей подготовки, всех форм обучения / В.Г. Ланских. – Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2012. – 99 с.
- Майерс Г. Искусство тестирования программ / Г. Майерс, Т. Баджетт, К. Сандлер - М.: «Диалектика», 2012 - 272с.
- Меняев М.Ф. Информатика и базы программирования / М.Ф. Меняев - М.: Омега-Л, 2007 - 458с.
- Олифер, В. Г. Компьютерные сети. Принципы, технологии, протоколы: учеб. пос. / Олифер, В. Г., Олифер, Н. А. - 3-е изд. - СПб.: Питер, 2007. - 958c.: ил. - Библиогр.: с. 919-922. - ISBN 5-469-00504-6.
-
Волков В.Б. Информатика / В.Б. Волков, Н.В. Макарова - СПб.: Питер, 2011 - 576с. ↑
-
Майерс Г. Искусство тестирования программ / Г. Майерс, Т. Баджетт, К. Сандлер - М.: «Диалектика», 2012 - 272с. ↑
-
Меняев М.Ф. Информатика и базы программирования / М.Ф. Меняев - М.: Омега-Л, 2007 - 458с. ↑
-
Меняев М.Ф. Информатика и базы программирования / М.Ф. Меняев - М.: Омега-Л, 2007 - 458с. ↑
-
Гмурман, Владимир Ефимович. Теория вероятностей и математическая статистика: учеб. пособие / Гмурман, Владимир Ефимович. - 12-е изд., перераб. - М.: Высш. шк., 2008. - 479c. ↑
-
Волков В.Б. Информатика / В.Б. Волков, Н.В. Макарова - СПб.: Питер, 2011 - 576с. ↑
-
Волков В.Б. Информатика / В.Б. Волков, Н.В. Макарова - СПб.: Питер, 2011 - 576с. ↑
- Применение процессного подхода для оптимизации бизнес-процессов (теоретические основы применения процессного подхода)
- Ипотека в гражданском праве (Развитие ипотеки и история ее возникновения)
- Физические и юридические лица. Общее понятие (общие положения исследования)
- Физические и юридические лица в РФ. Общее понятие
- Страхование и его роль в развитии экономики (Теоретико-методические основы страхования)
- История и понятие системы программирования
- Понятие и виды наследования (Правовая характеристика)
- Задачи нотариата (Права, обязанности и ответственность)
- Отличия бухгалтерского учета от налогового учета (Теоретические аспекты основных различий налогового и бухгалтерского учета)
- Языки гипертекстовой разметки (Определение содержания основных понятий)
- Анализ и оценка средств реализации объектно-ориентированного подхода к проектированию экономической информационной системы(Применение структурного подхода при проектировании ИС )
- Особенности политики мотивации персонала корпораций

