Преподаватель который помогает студентам и школьникам в учёбе.

Основные структуры алгоритмов: сравнительный анализ и примеры их использования (Линейная алгоритмическая структура)

Содержание:

Введение

Актуальность исследования. Программирование занимает одну из значительных ниш в современном мире. Это не просто способ заставить работать компьютеры, но и поставить себя на путь развития своих способностей.

Нынешнее программирование многогранно и используется в таких важных сферах как строительство, бизнес и экономика, медицина, биология и физика. Большой процент физического труда в промышленности заменен на машинный и роботизированный труд, который управляется посредством программного обеспечения, что обеспечивает существенный прирост скорости, точности операций и эффективности производства. Такое богатство разнообразия применений обеспечивается солидным выбором языков программирования, которые позволяют пошагово описывать процесс решения задач различного уровня и сложности.

Составление такого пошагового описания процесса решения задачи называется алгоритмизацией, а алгоритмом называется конечный набор правил, расположенных в определённом логическом порядке, позволяющий исполнителю решать любую конкретную задачу из некоторого класса однотипных задач. В разных ситуациях в роли исполнителя может выступать электронное или какое-либо иное устройство или человек (например, военнослужащий, охраняющий склад боеприпасов и действующий согласно алгоритмам, записанным в устав караульной службы).

Целью данной работы является изучение основных структур алгоритмов.

Для достижения поставленной цели необходимо решить следующие задачи:

- раскрыть понятие алгоритма и его свойства;

- рассмотреть способы описания алгоритмов;

- провести сравнительный анализ различных видов алгоритмических структур;

- привести примеры использования основных структур алгоритмов.

Предметом работы является использование основных структур алгоритмов в конкретных примерах и программах.

Структура работы состоит из введения, трех глав, заключения и списка использованной литературы.

Теоретической и методологической базой для написания работы послужили труды отечественных и зарубежных авторов в области программирования и алгоритмизации, а также межгосударственные стандарты (ГОСТ) Российской Федерации.

Основными источниками, раскрывающими теоретические основы алгоритмизации и программирования, явились работы А.В. Затонского, Н.В. Бильфельд, Д.Р. Кувшинова, И.Г. Семакина, С.В. Симонович, В.В. Трофимова, И.В. Черпакова.

Основы программирования на языке Паскаль наиболее полно раскрываются в работах А.В. Абрамян, М.Э. Абрамян, О.А. Авдеюк, Л.Г. Акулова, В.Ю. Наумова, Н.Д. Угринович.

В учебнике В.И. Медведик «Практика программирования на языке Паскаль» автор на конкретных примерах показывает профессиональный подход к стилю программирования, к надежности и корректности алгоритмов и программ.

В учебном пособии И.Г. Фризен И.Г. «Основы алгоритмизации и программирования (среда PascalABC.Net)» раскрываются основные положения языка Паскаль и описываются разнообразные приемы программирования.

Оценка надежности использованных источников:

1. Надежный источник (1, 2, 4, 6, 7, 9-18, 20, 22) - 74%

2. Довольно надежный источник (3, 8, 23) - 13%

3. Не всегда надежный источник (5, 19, 21) - 13%

4. Ненадежный источник - 0%

1. Теоретические основы алгоритмов

1.1. Понятие алгоритма и его свойства

Практически все в нашем мире подчиняется каким-то законам и правилам. Современная наука не стоит на месте, благодаря чему человечеству известна масса формул и алгоритмов, следуя которым, можно рассчитать и воссоздать множество действий и строений, созданных природой, и воплотить в жизнь идеи, придуманные человеком.

Понятие «алгоритма» появилось в Европе в средние века, когда у европейских ученых появилась книга средневекового математика Мухаммеда бен Муса Аль Хорезми [17, c. 9].

Его родина - древнее государство Хорезм, город Хивы. Хорезми занимал территорию, которая сейчас находится на территории современных Узбекистана (Хорезмская и Каракалпакская области) и Туркменистана (Ташаузская область).

Условно датами рождения и смерти Аль Хорезми считаются 783 и 850 годы. В некоторых книгах Аль Хорезми назван Аль Маджуси, то есть маг. Отсюда многие исследователи делают вывод, что предки Аль Хорезми были жрецами зороастрийской религии.

Аль Хорезми был призван для работы в новую столицу халифат Багдад, где и жил до конца жизни. Свои труды он писал на арабском языке.

В первой половине XII века книга Аль Хорезми в латинском переводе проникла в Европу («Algoritmi de numero Indorum» («Индийское искусство счёта, сочинение Аль Хорезми»).

В этой книге описано, как правильно записывать натуральные числа, используя арабские цифры, и приведено описание алгоритма действий столбиком над такими числами. Эта книга стала настольной для всех средневековых математиков, и она дала всем современным языкам два новых слова: алгебра из «аль-джебр» и алгоритм из «аль-хорезми».

Конечно, слово «аль-хорезми» не очень похоже на слово «алгоритм», но это издержки греческого перевода. (Al - Gorethmi - так это примерно было написано по-гречески).

Для европейцев сначала алгоритм означал лишь нумерацию, а только потом значительно позже перерос в правило.

В учебнике «Информатика и информационные технологии» дано следующее определение алгоритма: «Алгоритм - понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящих от исходных данных к искомому результату» [18, c. 32].

В современной информатике и математике этот термин имеет еще и такие определения:

- последовательность действий, в которой строго определены правила выполнения;

- предписание, определяющее последовательность и содержание операций, выполняя которые, исходные данные приходят к искомому результату;

- точное описание какого-либо вычислительного процесса или любой другой последовательности действий;

- максимально полное и точное предписание о последовательности выполнения конечного количества действий, которые необходимы для благоприятного решения любой задачи схожего типа.

Словарь Ожегова дает такое определение алгоритма: алгоритм – это «совокупность действий, правил для решения данной задачи» [11, c. 97].

В ГОСТ 33707-2016 (ISO/IEC 2382:2015) «Информационные технологии (ИТ). Словарь» понятие алгоритма расписывается так: алгоритм – это «конечное упорядоченное множество точно определенных правил для решения конкретной задачи» [1].

В ГОСТ 34.003-90 «Информационная технология (ИТ). Комплекс стандартов на автоматизированные системы. Автоматизированные системы» уточняется, что алгоритм – это «конечный набор предписаний для получения решения задачи посредством конечного количества операций» [2].

Таким образом, алгоритм представляет собой точное описание определенного процесса, инструкцию по его выполнению.

Процесс разработки алгоритма - достаточно сложный и трудоемкий. Можно также сказать, что алгоритм представляет собой конечную последовательность команд для исполнителя, направленную на достижение конкретной цели.

Цель же, в свою очередь, является достижением желаемого результата.

В качестве исполнителя могут выступать люди, живые существа, автоматические устройства, способные к исполнению и восприятию команд.

Перечень команд, воспринимаемых и выполняемых (по возможности) исполнителем, называют системой команд.

Каждый алгоритм предназначен для конкретного исполнителя. Исполнение алгоритма начинается с первой команды. После того, как ее исполнили, переходят к следующей команде и так до конца алгоритма.

В качестве примера алгоритма можно вспомнить известный всем со школы арифметический способ сложения двух положительных чисел «столбиком». Алгоритм данной задачи представим в виде системы следующих действий [9, c. 13]:

- выделим в слагаемых разряды единиц и сложим единицы;

- при получении суммы меньшей 10 запишем ее в разряде единиц под нижним числом;

- при получении суммы большей или равной 10 запишем в разряде единиц только количество единиц, затем выделим в слагаемых разряд десятков и запишем полученный при сложении единиц десяток над разрядом десятков первого (верхнего) слагаемого;

- сложим десятки и т. д.

Аналогичные указания дают для сложения единиц других разрядов числа. Системой-исполнителем этого алгоритма может стать как ЭВМ, так и человек.

Понятие алгоритма в теорию и практику обучения вошло в конце 50-х годов прошлого столетия в связи с развитием программированного обучения и применением обучающимися машин.

Создание алгоритма требует творческого подхода, поэтому новый список последовательных действий может создать только живое существо. А вот для исполнения уже существующих инструкций фантазию иметь не обязательно, с этим справится даже бездушная техника.

Отличным примером точного исполнения заданной инструкции является пустая микроволновая печь, которая продолжает работать, несмотря на отсутствие пищи внутри нее.

Субъект или объект, которому не обязательно вникать в суть алгоритма, называется формальным исполнителем. Человек тоже может стать формальным исполнителем, однако в случае нерентабельности того или иного действия мыслящий исполнитель может все сделать по-своему. Поэтому основными исполнителями являются компьютеры, микроволновые печи, телефоны и другая техника.

Таким образом, понятие алгоритма в информатике имеет самое важное значение. Каждый алгоритм составляется с расчетом на конкретного субъекта, с учетом допустимых действий. Те объекты, к которым субъект может применить инструкции, составляют среду исполнителя.

Существует ряд определенных требований к алгоритмам. Перечислим некоторые важные свойства, которыми должен обладать каждый алгоритм [5, c. 5].

1) Массовость – это универсальность применения алгоритма к группе некоторых схожих задач, отличающихся только набором исходных данных. Исходные данные при этом могут выбираться из так называемой области применимости алгоритма.

2) Понятность подразумевает, что все правила алгоритма должны быть понятными и четкими. Тогда выполнение алгоритма приобретет необходимый механический характер без дополнительных указаний или сведений.

3) Дискретность (или раздельность, прерывность процесса) означает, что алгоритм представляет процесс решения задач в виде последовательного выполнения ранее определенных простых шагов. Каждое следующее действие может совершиться только после окончания предыдущего.

4) Конечность означает, что решение задачи необходимо получить за конечное число шагов.

5) Определенность означает, что компьютеру понятны лишь определенные и однозначные инструкции.

6) Эффективность означает, что для решения задачи необходимо использовать ограниченные ресурсы компьютера (объем оперативной памяти, процессорное время и т. д.).

Эффективность алгоритма определяют с учетом потребляемых ресурсов компьютера, к которым относят быстродействие (количество выполняемых операций и затраты трудоемкости на каждую из них) и общий объем оперативной памяти, которая выделяется под данные. Приведенные показатели могут иногда быть противоречивыми: так в результате повышения быстродействия могут потребоваться дополнительные расходы памяти и наоборот [6, c. 39].

При возможности улучшения одного показателя без ущерба для другого необходимо этого добиваться. В случаях, когда возникает дилемма, рекомендуется предпочесть экономию памяти в ущерб производительности, поскольку тактовая частота процессоров растет опережающими темпами по сравнению с объемами оперативной памяти.

Специалистами предлагается ряд мер для повышения эффективности.

1.2. Способы описания алгоритмов

Алгоритм моделирует решение задачи в виде точно определенной последовательности действий для некоторого исполнителя по преобразованию исходных данных в результирующие.

Для его описания используется алгоритмический язык – набор символов и правил образования и истолкования конструкций из этих символов для записи алгоритмов.

При записи алгоритмов решения задач можно применять изобразительные способы, представленные в виде [14, c. 67]:

словесно-формульного описания;
блок-схемы (используются для описания графические символы);
алгоритмических языков;
операторных схем;
псевдокодов.

Запись алгоритмов осуществляется по общей методике [14, c. 68]:

1. Любому алгоритму присваивается имя, раскрывающее его смысл.

2. Обозначаются начало и конец алгоритма.

3. Описываются входные и выходные данные.

4. Указываются команды, позволяющие выполнять определенные действия над выделенными данными.

Таким образом, алгоритм имеет общий вид, состоящий из следующих разделов:

названия;
описания данных;
начала;
команд;
конца.

При формульно-словесном способе записи алгоритмов описание данных выполняется с помощью формул и слов. Последовательность этапов выполнения алгоритма записывают в произвольной форме на естественном профессиональном языке той предметной области, для которой он строится.

Пусть, например, необходимо найти значение следующего выражения:

у = 2а - (х + 6).

Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:

1.Ввести значения а и х.

2.Сложить х и 6.

3.Умножить а на 2.

4.Вычесть из 2а сумму (х+6).

5.Вывести у как результат вычисления выражения.

Второй, наиболее распространенный графический способ описания алгоритмов, так называемая блок-схема. Название блок-схемы стали использовать, поскольку при графическом описании алгоритма используют схемы или блочные символы (блоки), соединяемые линиями связи.

Все этапы вычислительного процесса представляются в виде геометрических фигур (блоков) [16, c. 110].

Между блоками начала и конца алгоритма размещаются остальные блоки алгоритма.

Операторный блок (блок действия) содержит команды обработки данных.

Блок проверки условия предполагает два варианта дальнейшего развития решения задачи, в зависимости от того или иного выполнения поставленного условия.

Блоки ввода или вывода данных. Для выполнения алгоритма необходимы не только команды, но и данные, поступающие из вне. Для получения этих данных используется блок ввода. Для того чтобы можно было вывести результат выполнения программы, либо какое-нибудь сообщение используют блок вывода.

Порядок выполнения этапов указывают стрелками, которые соединяют блоки. Размещение геометрических фигур выполняется слева направо и сверху вниз. Нумеруют блоки в порядке их размещения в схеме.

Перечисленные выше блоки приведены в Приложении 1 [16, c. 96].

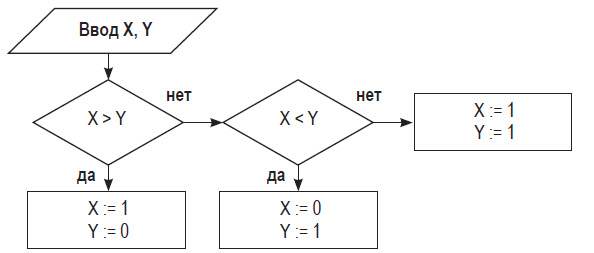
Рассмотрим пример. Алгоритм целочисленных преобразований представлен в виде фрагмента блок-схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1. Необходимо определить результат работы алгоритма для исходных данных Х = 7, Y = 12 (Приложение 2.) [16, c. 100]

Проведем решение.

1. Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).

2. В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».

3. Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».

4. Вычисляется результат выполнения алгоритма: X := 0, Y := 1.

Ответ: X := 0, Y := 1.

Третий способ описания алгоритмов - алгоритмический язык. Он представляет собой специальное средство, которое предназначено для записи алгоритма в аналитическом виде [21]. Данный тип языка близок к естественным языкам и к математическим выражениям. В каждом алгоритмическом языке имеется свой словарь. Для записи алгоритма на любом алгоритмическом языке используются строгие правила этого конкретного языка.

Алгоритмический язык программирования - формальный язык, используемый для записи, реализации и изучения алгоритмов. В отличие от большинства языков программирования, алгоритмический язык не привязан к архитектуре компьютера, не содержит деталей, связанных с устройством машины.

Для изучения основ алгоритмизации применяется так называемый Русский алгоритмический язык (школьный алгоритмический язык).

Алголо-подобный алгоритмический язык с русским синтаксисом был введён в употребление академиком А. П. Ершовым в середине 1980-х годов, в качестве основы для «безмашинного» курса информатики [22, c. 48].

Рассмотрим основные служебные слова алгоритмического языка.

1. Описание алгоритма:

алг (алгоритм)
арг (аргумент)
рез (результат)
нач (начало) — начало алгоритма
кон (конец) — конец алгоритма
дано — исходные данные в произвольной форме
надо — цель алгоритма
утв

2. Типы данных:

цел (целый)
вещ (вещественный)
сим (символьный)
лит (литера) — строка
лог (логический)
таб (таблица) — для обозначения массива
длин (длина) — количество элементов массива

3. Обозначение условий:

если
то
иначе
все
выбор
при
знач

4. Обозначение циклов:

нц (начало цикла)
кц (конец цикла)
пока
для
от
до
шаг

Логические функции и значения для составления выражений:

и
или
не
да
нет

Ввод-вывод:

ввод
вывод

Общий вид алгоритма выглядит так [19]:

1 алг название алгоритма (аргументы и результаты)

2| дано условия применимости алгоритма

3| надо цель выполнения алгоритма

4 нач описание промежуточных величин

5| последовательность команд (тело алгоритма)

6 кон

Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон - телом алгоритма.

В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное граничными парами по каждому индексу элементов массива.

В записи алгоритма ключевые слова обычно подчёркиваются либо выделяются полужирным шрифтом. Для выделения логических блоков применяются отступы, а парные слова начала и конца блока соединяются вертикальной чертой.

Далее приведем шаблоны составления этих структур на алгоритмическом языке [19].

Неполная развилка

1| если условие

2| | то действия

3| всё

Полная развилка

1| если условие

2| | то действия 1

3| | иначе действия 2

4| всё

Ветвление

1| выбор параметр

2| | при знач значение 1

3| | | действия 1

4| | при знач значение 2

5| | | действия 2

6| | иначе

7| | | действия по умолчанию

8| всё

Цикл с предусловием

1| нц пока условие

2| | действия

3| кц

Цикл с постусловием

1| нц

2| | действия

3| кц пока условие

Параметрический цикл

1| нц для параметр от НЗ до КЗ шаг Ш

2| | действия

3| кц

Если для выполнения параметрического цикла шаг принимается равным 1, то он может не указываться.

Рассмотрим пример составления алгоритма на алгоритмическом языке [9, c. 43].

Вычислить сумму квадратов целых чисел от 1 до n.

1 алг Сумма квадратов (арг цел n, рез цел S)

2| дано n > 0

3| надо S = 1*1 + 2*2 + 3*3 + … + n*n

4 нач цел i

5| ввод n

6| S:=0

7| нц для i от 1 до n

8| | S:=S+i*i

9| кц

10| вывод "S = ", S

11 кон

Четвертый способ описания алгоритмов - операторные схемы. Операторные схемы алгоритмов являются способом описания алгоритмов, при котором каждый оператор обозначают буквой (например, А – арифметический, Р – логический и т.д.).

Сами операторы записывают слева направо в порядке их выполнения, при этом у каждого оператора имеется индекс, который указывает на его порядковый номер. Алгоритм записывают одной строкой в виде последовательности операторов.

Обозначения операторов:

B - ввод исходных данных;

A - арифметический оператор;

П - оператор печати (вывода);

Р - логический оператор;

Я - оператор останова.

Логический оператор записывается как функция, аргументом которой служит проверяемое условие P (i = N) или (υ ≤ 0) и т.д.

Ввел этот метод А.А. Ляпунов в 1954 году. Операторные схемы имеют формальный уровень, близкий к алгоритмическим языкам, и поэтому могут рассматриваться как средство автоматизации программирования [20, с. 245].

Пятый способ описания алгоритмов – псевдокод - представляет собой систему команд абстрактной машины. Данный способ записи алгоритмов осуществляется с помощью операторов близких к алгоритмическим языкам [23, c. 125].

Приведем базовые управляющие структуры псевдокода:

- структура «присваивание, ввод, вывод» - переменная = 0, ввод (переменная), вывод (переменная);

- структура «ветвление» - если условие то (серия1 иначе серия 2);

- цикл ПОКА - пока условие нц серия кц.

Пример программы «Здравствуй, Мир!»

алг ЗДРАВСТВУЙМИР

нач

вывод ('Здравствуй, Мир!')

кон алг ЗДРАВСТВУЙМИР

Сделаем вывод, что алгоритм - это понятие, относящееся к фундаментальным основам информатики и обозначающее подборку инструкций, которые необходимо выполнять человеку для того, чтобы решить определенную задачу. Оно возникло задолго до появления компьютеров и является одним из основных понятий математики.

Основными свойствами алгоритма являются массовость, понятность, дискретность, конечность, определенность и эффективность.

Существуют различные способы описания алгоритмов. Основные из них - словесно-формульный (пошаговое описание), графический (в виде блок-схем), с использованием алгоритмических языков, операторных схем и псевдокода.

2. Сравнительный анализ алгоритмических структур

Алгоритмическая структура - это структура, где каждая часть предназначена для выполнения определенного алгоритма преобразования информации [17, c. 16]. Метод структурной алгоритмизации является одним из системных методов разработки алгоритмов. Он основан на визуальном представлении алгоритмов в виде последовательностей управляющих структурных фрагментов.

Каждый алгоритм состоит из элементарных шагов, которые можно объединить в определенные алгоритмические структуры:

- линейную (последовательную) структуру;

- разветвляющуюся структуру;

- циклическую структуру.

Проведем сравнительный анализ трех базовых алгоритмических структур: линейной, разветвляющейся и циклической структуры.

2.1. Линейная алгоритмическая структура

Линейной называется структура алгоритма, реализованная в виде последовательности действий, причем каждое действие выполняется только 1 раз, после каждого действия (шага) выполняется увеличение действия на 1 до тех пор, пока значение не станет больше конечного параметра алгоритма. Схема состоит последовательности блоков, расположенных сверху вниз в порядке их выполнения (Рис. 1) [17, c. 20].

Начало

Действие 1

Действие 2

Конец

Рис. 1. Линейная алгоритмическая структура

Данные первичного и промежуточного характера не влияют на направления процессов вычисления.

В Приложении 3 рассмотрен пример решения задачи с помощью блок-схемы линейного алгоритма. Задача: с = а* b (Приложение 3) [17, c. 21].

Таким образом, с помощью линейных алгоритмов представляют линейные процессы. Алгоритмы этого типа используют при описании обобщенного решения задач в виде последовательностей модулей.

2.2 Разветвляющаяся алгоритмическая структура

Разветвляющейся (ветвящейся) называют алгоритмическую структуру, обеспечивающую выбор между двумя вариантами решений в зависимости от значений входных данных [18, c. 298].

Ветвления бывают двух типов:

- неполное (если - то);

- полное (если – то - иначе).

В отличие от простой линейной структуры, с помощью полного ветвления можно организовать две ветви в алгоритме (то или иначе), каждая из которых приведет к общей точке их слияния, алгоритм будет выполняться независимо от того, по какому пути пошло решение.

При наличии неполного ветвления предполагаются некоторые действия алгоритма лишь на одной ветви (то), поскольку вторая отсутствует, для одного из результатов проверки действия производить нет необходимости, управление сразу перейдет к точке слияния.

Различают четыре варианта структуры ветвления:

1. Неполное ветвление типа «если – то», при котором все действия будут выполняться истинности условия.

2. Полное ветвление типа «если – то – иначе», при котором будут выполняться два действия в зависимости от истинности условия.

3. Ветвление с выбором типа «то», при котором действие 1 будет выполняться при условии 1, действие 2 при условии 2 и т.д.

4. Ветвление с выбором типа «иначе», при котором при условии 1 будет выполняться действие 1, при условии 2 действие 2 и т.д., а иначе будут выполняться все другие действия.

В Приложении 4 приведены блок-схемы разветвляющихся алгоритмов [18, c. 299].

В качестве примера составим алгоритм для вычисления функции: (X+1,Y>0) Z =

(X+Y, Y<0.)

Словесное описание разветвленного алгоритма имеет следующий вид:

1. Ввести X.

2. Если Y > 0, то Z = X + 1.

3. Если Y <0.

4. Вывести Z = X + Y.

5. Конец.

В Приложении 5 можно увидеть графическое изображение этого разветвленного алгоритма [13, c. 11].

Сделаем вывод, что разветвляющийся алгоритм - последовательность выполнения шагов алгоритма изменяется в зависимости от некоторых условий. В отличие от линейной структуры, в данном виде алгоритма может осуществляться выбор одного из двух/нескольких возможных вариантов. Разветвляющийся алгоритм содержит блок проверки некоторого условия, и в зависимости от результата проверки выполняется та или иная последовательность шагов (действий).

2.3 Алгоритмическая структура «Цикл»

Циклической (или циклом) называется структура алгоритма, в которой некоторая группа идущих подряд действий (шагов) выполняется несколько раз в зависимости от условия задачи и входных данных [15, c. 243]. Такую группу повторяющихся действий на каждом шагу цикла называют телом цикла. В любой циклической конструкции содержатся элементы ветвящейся конструкции алгоритма.

В отличие от линейного или разветвленного алгоритма, циклический алгоритм является более сложным по своей структуре и включает в себя описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие.

Различают три типа циклических алгоритмов:

- цикл с параметром (арифметический цикл – цикл типа для for);

- цикл с предусловием (цикл типа пока while);

- цикл с постусловием (цикл типа до repeat).

Рассмотрим арифметический цикл. Приведем блок-схему данного вида алгоритма (Рис. 2) [15, c. 244].

i, a, b, h

Серия команд

Рис. 2. Арифметический цикл типа для

В цикле данного типа число шагов однозначно определено правилом изменения параметра, задаваемом с помощью его начальных и конечных значений, а также шага его изменения. Т.е., на каждом шаге цикла значение параметра изменяется согласно шагу цикла, пока не достигнет значения, равного конечному значению параметра.

Рассмотрим второй тип циклического алгоритма - цикл с предусловием. В данном цикле количество шагов заранее не определяется, оно зависит от входных данных (Рис. 3) [15, c. 244].

Нет

Условие

Да

Серия команд

Рис. 3. Цикл с предусловием типа пока

В этой циклической структуре сначала происходит проверка значения условного выражения (условия), стоящего перед выполнением очередного шага цикла. При истинном значении условного выражения будет исполняться тело цикла. После чего снова будет выполняться проверка условия. Эти действия будут повторяться до тех пор, пока значение условного выражения не станет ложным, тогда цикл завершится.

Особенностью данного типа цикла является то, что при изначальной ложности значения условного выражения тело цикла не будет выполняться совсем.

Рассмотрим третий тип циклического алгоритма - цикл с постусловием (Рис. 4) [15, c. 245].

В данной циклической конструкции, как и в предыдущей, заранее не определяется число повторений тела цикла, оно будет зависеть от входных параметров.

Серия команд

Условие

Да

Нет

Рис. 4. Цикл с постусловием типа до

Отличительной чертой цикла с предусловием от других видов циклической структуры является то, что тело цикла с постусловием в любом случае будет выполнено хотя бы один раз и только после этого проверится условие. В данной конструкции тело цикла выполняется до тех пор, пока значение условного выражения будет ложным. Как только оно станет истинным, выполнение команд прекратится.

В реальных задачах, как правило, присутствует любое количество циклов.

Для организации любого цикла необходимо следующее [13, c. 22]:

1. Задать перед началом цикла начальные значения параметров цикла.

2. Изменять параметры цикла перед каждым новым повторением цикла.

3. Проверять условие повторения или окончания цикла.

4. Переходить к началу цикла, если он не закончен, или выходить из цикла.

Необходимо отметить, что в отличие от структур (цикл типа пока и цикл типа до) цикл типа для имеет строго фиксированное число повторений, что позволяет избежать зацикливания, т. е. ситуации, когда тело цикла выполняется бесконечно.

Сделаем вывод, что основные алгоритмические структуры бывают линейного, разветвляющегося (полные и неполные) и циклического вида.

Проведя сравнительный анализ, мы выяснили, что линейные алгоритмы достаточно просты и используют структуру следование – такую алгоритмическую конструкцию, отображающую естественный, последовательный порядок действий. То есть в линейных алгоритмах команды выполняются в той последовательности, как записаны.

В отличие от линейных алгоритмов, разветвленные алгоритмы более сложны и содержат одно или несколько условий и в них, в зависимости от результата проверки условия («да» или «нет»), предусмотрен выбор одной из двух последовательностей действий (ветвей).

Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.

В свою очередь циклический алгоритм представляет собой структуру повторения - последовательность действий, выполняемых многократно. Для решения различных задач могут быть соединены циклический и разветвленные алгоритмы.

3. Примеры использования основных структур алгоритмов

3.1. Линейные программы

Линейными называются программы, состоящие из простых команд (операторов) ввода, математических расчетов (формул) и команд вывода результатов.

В программировании под оператором понимается некоторая операция, которая совершается над какими-то данными (операндами). Существует несколько видов операторов:

- унарные - операции с одним аргументом (инверсия, отрицание, смена знака и т.п.);

- бинарные - операции, которые производятся с двумя аргументами (сложение, вычитание, деление и т.п.);

- тернарные - операции, которые производятся с тремя аргументами.

Под командами в программировании понимают несколько другие действия. Например, к командам могут быть отнесены такие, как создать файл, изменить текущую директорию (каталог, папку), удалить, переименовать файл, включить «эхо», изменить атрибуты файлов и т.д.

В линейной программе на языке программирования Паскаль присутствуют три базовых блока [10, c. 12]:

1. Команды ввода данных

2. Математические расчеты

3. Вывод результатов.

Простыми командами (простыми указаниями алгоритма) называются команды, которые не используют условия в своем исполнении. К числу простых операторов принадлежат команды (операторы) присваивания, ввода и вывода данных, вызова вспомогательного алгоритма — подпрограммы.

Оператор/команда присваивания задает или изменяет значение определенной переменной. При этом изменяется содержание ячейки памяти, которая отведена для этой переменной.

Оператор присваивания: переменная := выражение;

где переменная - любая переменная (объявленная заранее в разделе описания переменных), выражение - соответствующее по типу выражение (например, целой переменной не может быть присвоено вещественное или символьное значение).

При выполнении этого оператора сначала вычисляется значение выражения, а затем это значение присваивается переменной.

Пример 1:

a:=1;

b:=a+2;

c:=’пример’

Слева от знака «:=» расположено имя переменной, справа — значение или имя другой переменной или выражение.

Операторы ввода данных: Read (список_переменныx);

где список_переменныx – перечень вводимых переменных, разделенных запятыми (объявленных заранее в разделе описания переменных).

При выполнении данного оператора пользователь с клавиатуры должен ввести значения указанных переменных. Значения должны соответствовать типам переменных, разделять их при вводе нужно пробелом или клавишей Enter. После выполнения курсор остается на той же строке [8, c. 32].

Пример 2:

Read(a);

Read(a,b);

Readln (список_переменныx);

где список_переменныx – список вводимых переменных, разделенных запятыми (объявленных заранее в разделе описания переменных).

Действие оператора аналогично предыдущему, но после выполнения курсор переводится на новую строку.

Операторы вывода данных: Write ('комментарий',список_переменныx);

где комментарий – необязательная текстовая часть, выводится на экран без изменения,список_переменных - перечень переменных, значения которых выводятся на экран. В качестве элемента списка можно использовать переменную или выражение. Вместо переменной или выражения выводится их значение на момент выполнения оператора вывода. После выполнения курсор остается на той же строке.

Пример 3:

Write('a=',a);

Write('сумма чисел ',a, ' и ',b, ' равна', c);

Writeln ('комментарий',список_переменныx);

где комментарий – необязательная текстовая часть, выводится на экран без изменения,список_переменных - перечень переменных, значения которых выводятся на экран.

Рассмотрим линейную программу [10, c. 223].

Руководитель проекта дал задание написать программу для расчета площади прямоугольного земельного участка со сторонами А = 25 единиц и В = 19,5 единиц.

Решение.

1. Математический решение задачи S = ab

2. Объявление переменных.Имена переменных программист вибирает сам, исходя из их смысла.

S-Area,

a-side_a,

b-side_b;

3. Типы переменных.

На данном этапе мы видим, что А — целое число (Integer); b- действительное число (Real). При умножении целого числа на действительное получим действительное. Итак Area — действительное число (Real);

1 Var side_a : Integer;

2 side_b, Area : Real;

3 BEGIN

4 side_a:=25;

5 side_b:=19.5;

6 Area := side_a * side_b;

7 Writeln('Area is =', Area:2:2);

8 Writeln('Press Enter to Exit');

9 readln;

10 END.

Для проверки наличия в программе синтаксических ошибок нажимаем F9. Для запуска программы на выполнение нажимаем Ctrl + F9.

Недостатком программы является то, что при изменении значений сторон земельного участка нужно каждый раз модифицировать программу. Так что нужно добавить команды на запрос данных от пользователя. А это выполняют команды ввода / вывода данных [10, c. 227].

1 Var side_a : Integer;

2 side_b, Area : Real;

3 BEGIN

4 Write('Side A='); Readln (side_a);

5 Write('Side B='); Readln (side_b);

6 Area := side_a * side_b;

7 Writeln('Area is =', Area:2:2);

8 Writeln('Press Enter to Exit');

9 readln;

10 END.

Объявление переменных начало программы.

Запрос значения стороны А. После введения числа нажимаем Enter. Число A переменной side_a.

Запрос значения стороны B. После введения числа нажимаем Enter. Число B переменной side_b.

Рассчитать площадь.

Вывести на экран сообщение Area is = и ее значение с двумя знаками после запятой (форматирование результата).

Сообщение, что нужно нажать Enter для выхода.

Завершение программы.

Тут необходимо отметить, что не всегда длина стороны А будет выражаться целым числом. Поэтому, чтобы обеспечить корректное выполнение программы для произвольных чисел нужно объявить переменную А как действительную [10, c. 230].

1 Var side_a : Real;

2 side_b: Real;

3 Area : Real;

4 BEGIN

5 Write('Side A=');

6 Readln (side_a);

7 Write('Side B=');

8 Readln (side_b);

9 Area := side_a * side_b;

10 Writeln('Area is =', Area:2:2);

11 Writeln('Press Enter to Exit');

12 readln;

13 END.

Рассмотрим еще один пример задачи.

Дан земельный участок прямоугольной формы со сторонами А и В. Цена 1 метра ограждения С рублей. Написать программу, которая будет рассчитать цену материала для ограждения [3].

Решение.

1. Чтобы рассчитать цену ограждения нужно найти периметр. P = 2 * (a + b);

2. Чтобы рассчитать цену материалов - нужно периметр умножить на цену за 1 метр ограждения. Сумма = периметр * цену или Сумма = (2 * (a + b)) * c.

Теперь рассмотрим переменные и их типы:

- стороны участка: А - side_a, B - side_b;

- цена – Cina;

- периметр - Perimetr.

Типы переменных: side_a. side_b действительные числа (Real), их длина выражаться не обязательно только в метрах (метр и сантиметр).

Cina - действительное число (Real), цена идет в рублях и копейках, даже если количество копеек равна нулю.

Perimetr - действительное число (Real), потому что складываем и умножаем действительные числа.

Summa – действительное число (Real).

Для расчета компьютер должен знать определенные данные. А именно: длины сторон, цену за 1 метр материала для ограждения. Итак, «входящими» данным для программы будут side_a, side_b, Cina.

Промежуточным результатом будет значение Perimetr.

Результатом будет Summa.

1 Var side_a : Real;

2 side_b: Real;

3 Perimetr : Real;

4 Cena : Real;

5 Summa : Real;

6 BEGIN

7 Write('Side A='); Readln (side_a);

8 Write('Side B='); Readln (side_b);

9 Write('Cina ='); Readln (Cena);

10 Perimetr :=2 * (side_a + side_b);

11 Summa := Cena * Perimetr;

12 Writeln('Money =', Summa:2:2);

13 Writeln('Press Enter to Exit');

14 readln;

15 END.

3.2. Программы с использованием ветвлений

В языке Паскаль имеется оператор ветвления. Другое его название — условный оператор. Формат полного оператора ветвления следующий:

if <логическое выражение> then <оператор1> else <оператор2>

Здесь if — «если», then — «то», else — «иначе».

Условие - это логическое выражение, от которого зависит выбор одной из двух альтернативных ветвей алгоритма. Если условие принимает значение true (истина), выполняется оператор1, помещенный за ключевым словом then. Иначе выполняется оператор2, записанный за ключевым словом else (в этом случае оператор1 опускается) [8, c. 23].

Когда указанные операторы выполнены, то программа переходит к выполнению команды, стоящей после оператора if.

Ключевое слово else может как присутствовать, так и отсутствовать в операторе if, например:

if <логическое выражение> then <оператор1>

Но тогда в случае, когда не выполнено логическое условие, то управление передается оператору, которые стоит в программе после конструкции if.

Отметим, что синтаксис языка Паскаль позволяет записать только один оператор после ключевых слов then и else, вследствие этого группа инструкций должна быть объединена в составной оператор (заключить между служебными слова begin и end). Иначе происходит логическая ошибка программы, и компилятор ошибок не выдает, однако программа все-таки работает неправильно [8, c. 24].

В процессе создания программы часто приходится производить выбор одного из нескольких альтернативных путей выполнения программы. Подобный выбор организуется при помощи оператора if. Однако для большего удобство используют другой специальный оператор выбора case либо с ключевым словом else.

Рассмотрим примеры сокращенного варианта ветвления [8, c. 24].

Пример 1. Пусть дано два числа А и В, которые не равны между собой. Найти максимальное число.

Решение.

If (a>b) then max:=a;

If (b>a) then max:=b;

1 var a, b:real;

2 max:real;

3 BEGIN

4 write('Nomber A=');readln(a);

5 write('Nomber B=');readln(b);

6 If (a>b) then max:=a;

7 If (b>a) then max:=b;

8 Writeln('Max nomber is', max);

9 write('Press Enter to Exit');

10 readln;

11 END.

Пример 2. Дано два числа А, В неравных между собой. Найти разницу между большим и меньшим числом.

1 var a, b:real;

2 resalt:real;

3 BEGIN

4 write('Nomber A=');readln(a);

5 write('Nomber B=');readln(b);

6 If (a>b) then begin

7 resalt:=a-b;

8 writeln('Resalt=',resalt);

9 end;

10 If (b>a) then begin

11 resalt:=b-a;

12 writeln('Resalt=',resalt);

13 end;

14 Write('Press Enter to Exit');

15 readln;

16 END.

Далее рассмотрим примеры полного варианта ветвления.

Пример 1. Пусть дано два числа А и В, которые не равны между собой. Найти максимальное число [4, c. 98].

If (a>b) then max:=a else max:=b;

Полное решение задачи:

1 var a, b:real;

2 max:real;

3 BEGIN

4 write('Nomber A=');readln(a);

5 write('Nomber B=');readln(b);

6 If (a>b) then max:=a else max:=b;

7 Writeln('Max nomber is', max);

8 write('Press Enter to Exit');

9 readln;

10 END.

Пример 2. Дано два числа А, которые не равны между собой. Найти разницу между большим и меньшим числом.

1 var a, b:real;

2 resalt:real;

3 BEGIN

4 write('Nomber A=');readln(a);

5 write('Nomber B=');readln(b);

6 If (a>b) then begin

7 resalt:=a-b;

8 writeln('Resalt=',resalt);

9 end else begin

10 resalt:=b-a;

11 writeln('Resalt=',resalt);

12 end;;

13 Write('Press Enter to Exit');

14 readln;

15 END.

Таким образом, чтобы оптимизировать программы ветвлений, мы вместо двух команд If использовали слово Else и экономили одну строку. Для того чтобы еще сократить программный код, используется команда выбора «Case» [4, c. 101].

Общая структура команды выглядит так:

1 case Выражение of

2 значение1 : оператор (группа операторов);

3 значение2 : оператор (группа операторов);

4. . . . . . . . . . . . . . . . . . . . . .

5 значениеN : оператор (группа операторов)

6 else оператор (группа операторов);

7 end;

Оператор выбора работает следующим образом. Для начала вычисляется значение выражения, которое находится после зарезервированного слова case, а затем выполняется команда (или набор команд), которая соответствует результату выражения.

Бываю случаи, что в списке выбора не окажется значения, которое равно вычисленному значению в команде Case. В этом случае управление передается набору команд, стоящих после слова else. Если else отсутствует, то в этом случае просто ничего не выполняется [4, c. 99].

Если один оператор выполняется при нескольких значениях проверяемой переменной, то их можно перечислить через запятую.

Рассмотрим пример: По номеру месяца указать квартал.

1 var n_month:byte;

2 Begin

3 write('N month='); readln(n_month);

4 case n_month of

5 1, 2, 3 : writeln ('Первый квартал');

6 4, 5, 6 : writeln ('Второй квартал');

7 7, 8, 9 : writeln ('Третий квартал');

8 10, 11, 12 : writeln ('Четвёртый квартал');

9 end;

10 writeln('Press Enter to Exit');

11 Readln;

12 End.

Если оператор должен выполняться при нескольких последовательных значениях проверяемой переменной, образующих некоторый промежуток, можно использовать следующую форму записи:

1 var n_month:byte;

2 Begin

3 write('Номер месяца='); readln(n_month);

4 case n_month of

5 1..3 : writeln ('Первый квартал');

6 4..6 : writeln ('Второй квартал');

7 7..9 : writeln ('Третий квартал');

8 10..12 : writeln ('Четвёртый квартал');

9 end;

10 writeln('Press Enter to Exit');

11 Readln;

12 End.

3.3. Программы с использования циклов

При решении большинства задач определенные последовательности действий необходимо выполнять не одно число раз. К примеру, для обнаружения чьей-либо фамилии в списке, нужно перебирать все фамилии пока не найдем нужную, или не дойдем до конца списка. Подобные повторяющиеся действия называют циклами и реализуют в программе с помощью специальных инструкций.

В среде программирования Паскаль используют три вида циклических операторов [15, c. 301]:

- while - оператор цикла с предварительным условием (с предусловием);

- repeat - оператор цикла с последующим условием (с постусловием);

- for - оператор цикла с управляющим параметром (с параметром).

Рассмотрим оператор цикла While. Для цикла с предусловием характерна проверка условия перед выполнением цикла. Если условие носит истинный характер, то будет выполняться продолжение цикла, иначе - цикл завершится.

Синтаксис оператора: while < логическое_выражение > do < оператор >;

где < оператор > представляет собой оператор, который может быть простым или составным, а < логическое_выражение > представлено выражением булевого типа.

Действия оператора цикла while заключаются в следующем [3]:

- вначале выполняется проверка значения логического выражения, пока оно будет истинным, выполняется < оператор >, указанный после do. В случае изменения значения логического выражения на ложное выполняется выход из цикла;

- если изначально логическое выражение ложно, то < оператор > не выполнится ни разу. В случае, когда логическое выражение будет истинным постоянно, цикл станет выполняться до бесконечности долго.

Базовая структура команды While:

1 параметр_флаг:=начальное значение

2 While (условие истинно=true) do

3 begin

4 Действия; изменение параметра_флага условия;

5 end;

Рассмотрим пример. Вывести на экран числа от 1 до 10.

1 var i:integer;

2 BEGIN

3 i:=1; //начальное значение

4 While i<=10 do // условие выхода

5 begin

6 write(i:3);

7 i:=i+1; //изменение параметра выхода

8 end;

9 Write('Press Enter to Exit...');

10 readln;

11 END.

Рассмотрим оператор цикла For. Для цикла с параметром характерно определение количества исполняемых циклов в операторе for.

Синтаксис оператора: for i:= n1 to n2 do.

где i - переменная (параметр) цикла; n1, n2 - начальное и конечное значения переменной цикла.

В качестве параметра i может использоваться только простая переменная, а в качестве n1, n2 используются выражения кроме выражений вещественного типа (real). Параметры i, n1, n2 должны быть одинакового скалярного, но не вещественного типа, т.е. могут быть целыми, символьными, ограниченного типа или перечисляющего [3].

Параметр цикла i примет последовательно значения указанного типа от n1 до n2. Если i, n1, n2 – переменные целого типа, то они всегда будут изменяться с шагом +1.

Убывающий цикл по значениям параметра i от n1 до n2 можно записать, используя следующий оператор: for i := n2 downto n1 do < оператор >; При этом параметр i последовательно будет принимать убывающие значения указанного типа от n2 до n1.

Необходимо обратить внимание на переменную I [3].

В For — переменная счетчик может быть только целого (integer) типа.

В While — она может быть целого (integer), действительного (real) и логического (boolean) типов.

Переменную, которая имеет тип boolean называют Флагом. Эта переменная может получать значения True или False.

Пример. Вывести на экран числа от 1 до 15.

1 var i:integer;

2 begin

4 for i:=1 to 15 do

5 write(i,' ');

7 Writeln('Press Enter to Exit');

8 readln;

9 end.

Обратный пример. Вывести на экран числа от 15 до 1

1 var i:integer;

2 begin

4 for i:=1 downto 15 do

5 write(i,' ');

7 Writeln('Press Enter to Exit');

8 readln;

9 end.

Рассмотрим оператор цикла Repeat.

В состав оператора повтора repeat входят заголовок (repeat), тело цикла и условие окончания (until). Для цикла с постусловием характерно обязательное выполнение вначале хотя бы одного раза команды, входящей в цикл [3].

По завершении цикла проверяется условие. При ложном условии операторы цикла выполняются снова. При истинности условия - цикл завершается.

Синтаксис оператора: repeat < оператор_1 >; < оператор_2 >; ........... < оператор_n > until < логическое_выражение >;

где < логическое_выражение > (условие) - выражение булевого типа.

При записи условия допускается использование булевых операций, а также операций отношения. При этом операторы, стоящие между repeat и until, составляют тело цикла.

Оператор цикла repeat выполняется следующим образом [4, c. 105]:

- вначале происходит выполнение операторов цикла, проверка значения логического выражения: при его ложности снова будут выполняться операторы цикла; при истинном значении цикл заканчивается;

- при изначальной истинности логического выражения операторы цикла выполняются только 1 раз. В случае, когда логическое выражение вовсе не принимает истинного значения, операторы цикла будут выполняться бесконечно долго, т.е. речь идет о так называемом зацикливании;

- нижняя граница операторов цикла четко обозначается ключевым словом until, в связи с этим операторы не заключаются в операторные скобки begin - end. Но, если вы написали дополнительно операторные скобки, это не будет являться ошибкой.

Для выхода из цикла раньше времени используется оператор goto.

Пример. Вычислить корень квадратный из введенного с клавиатуры числа. При вводе отрицательного числа каждый раз компьютер будет возвращать в начало цикла, поскольку выйти из цикла можно, если ввести неотрицательное число x: x >= 0.

1 var

2 x: integer;

4 begin

5 repeat

6 readln(x)

7 until x >= 0; { <-- выходим, если x>=0 }

8 writeln('Квадратный корень: ', sqrt(x):0:4);

9 readln

10 end.

Сделаем вывод, что различают следующие виды алгоритмических программ: линейные программы, когда список команд (указаний), выполняемых последовательно друг за другом; программы с использование ветвлений, это когда алгоритм, содержащий хотя бы одну проверку условия, в результате которой обеспечивается переход на один из возможных вариантов решения; и программы с использованием циклов, это когда алгоритм, предусматривающий многократное повторение одной и той же последовательности действий. Количество повторений обусловливается исходными данными или условием задачи.

Любая алгоритмическая конструкция может содержать в себе другую конструкцию того же или иного вида, т. е. алгоритмические конструкции могут быть вложенными.

Заключение

В заключении работы приведем следующие выводы. Алгоритм является фундаментальным понятием информатики. Представление о нем необходимо для эффективного применения вычислительной техники к решению практических задач.

Алгоритм обладает некоторыми важными свойствами, которые отличают его от любых других предписаний.):

- понятность (для конкретного исполнителя);

- дискретность (команды последовательны, с точной фиксацией моментов начала и конца выполнения команды);

- точность (после выполнения каждой команды точно известно, завершено ли исполнение алгоритма или же какая команда должна выполниться следующей);

- результативность (после конечного числа шагов задача решается или же становится ясно, что процесс решения не может быть продолжен):

- массовость (алгоритм единым образом применяется к любой конкретной формулировке задачи, для которой он разработан).

Для создания алгоритма необходимо знать полный набор исходных данных задачи (начальное состояние объекта), цель создания алгоритма (конечное состояние объекта), а также систему команд исполнителя (то есть набор команд, которые исполнитель понимает и может выполнить).

Проведя сравнительный анализ и рассмотрев примеры использования алгоритмов, мы выяснили, что программа абсолютно любой сложности строится всего на трех алгоритмических структурах: линейной, разветвленной и циклической.

Линейные алгоритмы достаточно просты и используют структуру следование – такую алгоритмическую конструкцию, отображающую естественный, последовательный порядок действий. То есть в линейных алгоритмах команды выполняются в той последовательности, как записаны.

Циклический алгоритм является важнейшей и более сложной структурой повторения, которая применяется в любой полноценной программе - последовательность действий, выполняемых многократно. Для решения различных задач могут быть соединены циклический и разветвленные алгоритмы.

Сколько существует различных задач, столько существует и различных способов написания алгоритмов для их решения. Тем не менее есть большая вероятность того что задача которую необходимо решить в некотором смысле похожа на другую задачу. Развивая глубокое понимание основных структур алгоритмов, можно выбрать верный алгоритм и применить его для решения задачи. Чем более точно и однозначно будут описаны правила решения задач, тем быстрее человек овладеет ими и будет эффективнее их применять.

Список использованных источников

ГОСТ 33707-2016 (ISO/IEC 2382:2015) Информационные технологии (ИТ). Словарь. - М.: Стандартинформ, 2016
ГОСТ 34.003-90 Информационная технология (ИТ). Комплекс стандартов на автоматизированные системы. Автоматизированные системы. Термины и определения. - М.: Стандартинформ, 2019
Абрамян А.В., Абрамян М.Э. Основы программирования на языке Паскаль в задачах. Электронное учебное пособие. - Ростов-на-Дону: ЮФУ, 2017
Авдеюк О.А., Акулов Л.Г., Наумов В.Ю. Информатика и программирование: основы программирования на языке Паскаль: учебно-методическое пособие. — 2-е изд., исправл. — Волгоград: Волгоградский государственный технический университет, 2018. — 268 с.
Алгоритм. Способы описания алгоритма. Учебно-методическое пособие для учителей информатики / сост. Е.А.Пархоменко, Ю.В.Сюбаева – Коломна: Лицей, 2017. – 33 с.
Затонский А.В., Бильфельд Н.В. Программирование и основы алгоритмизации. Теоретические основы и примеры реализации численных методов. - М.: Изд-во РИОР, 2019. - 167 с.
Кувшинов Д. Р. Основы программирования: учебное пособие для вузов / Д. Р. Кувшинов. — М.: Издательство Юрайт, 2019; Екатеринбург: Изд-во Урал. ун-та. — 104 с.
Кудрец Д. М. Основы программирования на языке Pascal: учебное пособие. - М.: Программирование, 2018. - 50 с.
Кузнецов А.А. Основы информатики: учеб. для общеобразоват. учеб. заведений / А.А.Кузнецов, Н.В.Апатова. - М.: Дрофа, 2016. - 176 с.
Медведик В. И. Практика программирования на языке Паскаль. Задачи и решения. - М.: Изд-во ДМК-Пресс, 2017. - 590 с.
Ожегов С. И. Толковый словарь русского языка. - М.: Мир и образование, 2019. - 1376 с.
Основы программирования. Учебник с практикумом / под ред. Макаровой Н.В. - М.: КноРус, 2017. - 352 c.
Парфилова Н.И. Программирование: Основы алгоритмизации и программирования: учебник / Н.И. Парфилова / под ред. Трусова Б.Г. - М.: Academia, 2018. - 32 c.
Семакин И.Г. Основы алгоритмизации и программирования. Учебник / И.Г. Семакин, А.П. Шестаков. - М.: Academia, 2017. - 144 c.
Симонович С. В. Информатика. Базовый курс. Учебник для вузов. - СПб.: Изд-во Питер, 2019. - 640 с.
Трофимов В. В. Информатика в 2 т. Том 1: учебник / В. В. Трофимов; под редакцией В. В. Трофимова. — 3-е изд., перераб. и доп. — М.: Издательство Юрайт, 2019. — 553 с.
Трофимов В. В. Основы алгоритмизации и программирования: учебник / В. В. Трофимов, Т. А. Павловская; под редакцией В. В. Трофимова. — М.: Издательство Юрайт, 2018. — 137 с.
Угринович Н.Д. Информатика и информационные технологии. - М.: 2018. — 512 с.
Филиппов Е.С. Разработка учебного алгоритмического языка для обучения школьников основам алгоритмизации и программирования // Информатика. 2018. № 6
Фризен И.Г. Основы алгоритмизации и программирования (среда PascalABC.Net): учебное пособие / И.Г. Фризен. - М.: Форум, 2018. - 784 c.
Чернышов П. И. Программная реализация задач средствами алгоритмических языков // Информатика. 2018. №12.
Черпаков И. В. Основы программирования: учебник и практикум / И. В. Черпаков. — М.: Издательство Юрайт, 2019. — 219 с.
Шень А. Программирование: учебное пособие. Издание: 6-е, дополненное. — М.: МЦНМО, 2017. — 320 с.

Приложения

Приложение 1

Блок-схемы при графическом способе описания алгоритма

Начало и конец алгоритма
Ввод исходных данных, вывод результатов
Какое-либо действие (вычисление, сложение и так далее)
Проверка условия

Приложение 2

Пример блок-схемы

Приложение 3

Линейный алгоритм для решения задачи с = а* b

Начало Ввод данных с = а * b Вывод с Конец алгоритма	Начало алгоритма
	Ввод данных
	Процесс выполнения действий
	Вывод данных
	Конец алгоритма

Приложение 4

Полное ветвление

Условие

Действие 1

Действие 2

Действие 3

Неполное ветвление

Условие

Действие 1

Действие 2

Приложение 5

Пример графического изображение разветвленного алгоритма

Начало

Ввод Х

Y > 0

Да

Нет

Z = X + 1

Z = Y + X

Вывод Z

Конец