Описание свойств векторных полей (Градиент)

Содержание:

Введение

Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени различен в разных точках и может быть описан векторным полем.

Материальный аппарат теории поля – векторный анализ. Будем говорить, что нам задано поле некоторой величины, если во всех точках рассматриваемого объема нам задано значение этой величины.Если в каждой точке 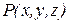 пространства или некоторой среды задана скалярная функция  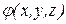, то говорят, что задано скалярное поле. Если величина векторная, то говорят, что задано векторное поле.

Градиент

По определению градиентом скалярной функции 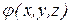 называется вектор

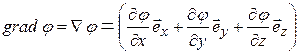 . (13.01)

Следует помнить о том, что градиента векторной функции не существует, в силу того, что он просто не определен. Можно рассматривать градиент модуля вектора, но модуль – это скалярная величина.

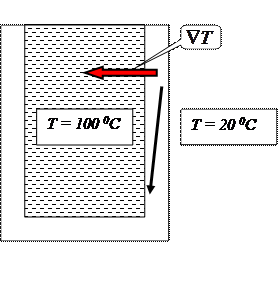 Физический смысл градиента функции заключается в том, что это вектор, направленный в сторону скорейшего возрастания функции, а по модулю равный производной, взятой вдоль направления скорейшего возрастания.

НАПРИМЕР, если в стакан налит кипяток, то, очевидно, что в стенках стакана устанавливается градиент температуры. Поскольку градиент направлен в сторону скорейшего возрастания величины, то градиент температуры перпендикулярен стенкам стакана. Температура изменяется и вдоль направления черной стрелки, но направление СКОРЕЙШЕГО возрастания задается, очевидно, красной.

Величину градиента грубо можно оценить, разделив известное изменение величины на расстояние на котором оно происходит, если это расстояние в направлении скорейшего изменения.

Пока стенки не прогрелись по толщине, можно считать, что на внутренней поверхности температура 100 ⁰С, а на внешней – в соответствии с температурой окружающей среды – 20⁰С. Если толщина стенок 1 мм, то градиент по модулю равен 80 ⁰С/мм = 8 10^{4 0}С/м. По мере прогревания стенок температура воды в стакане немного упадет, но на внешней поверхности – сильно возрастет. Разница температур уменьшится и градиент по модулю тоже.

Сравним понятия градиент и скорость. Когда мы говорим «скорость изменения некоторой величины равна…», то обычно подразумеваем, что речь о быстроте изменения величины во времени. Говоря о том, что градиент некоторой величины составляет столько-то, мы говорим о быстроте изменения величины в пространстве, т.е. при изменении пространственных координат.

Поток вектора

Понятие векторного анализа наиболее наглядны при рассмотрении поля вектора скорости текущей жидкости. Собственно они и возникли в процессе развития гидродинамики, и этим обусловлена терминология, используемая в векторном анализе.

Рассмотрим течение идеальной жидкости, т.е. жидкости несжимаемой, молекулы которой взаимодействуют абсолютно упруго.

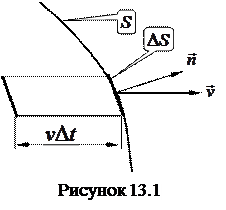
По определению, объемжидкости, протекающий в единицу времени через некоторую воображаемую поверхность называется потоком жидкости через S. Пусть скорость направленного движения частиц жидкости, пересекающих поверхность 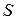 , равна  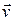. Выделим мысленно на поверхности элемент  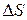и будем считать, что он настолько мал, что в его пределах скорость направленного движения частиц жидкости одинакова. Ориентацию в пространстве этого элемента зададим ортом нормали к нему  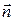. 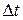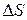За время  через  пройдет жидкость, заключенная в объеме

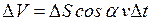  (13.02)

 Следовательно, по определению потока, элементарный поток через  :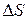

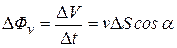 (13.03)

Устремив размеры элемента поверхности 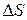 к нулю (  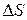→ 0), получим соотношение:

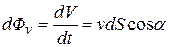 (13.04)

Формула (13.04) в соответствии с определением скалярного произведения векторов эквивалентна следующим:

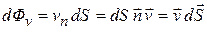 . (13.06)

Тогда поток жидкости через всю поверхность 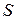 должен определяться соотношением:

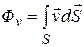 (13.07)

Распространив этот подход на все векторные поля, можем сформулировать определение потока произвольного вектора 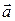 через поверхность  :

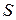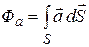 (13.08)

Основные свойства потока вектора: скалярная алгебраическая величина, знак которой зависит от выбора направления нормали к  .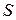

В случае замкнутых поверхностей всегда используется внешняя нормаль.

Чтобы продвинуться дальше в изучении электрического поля, необходимо ознакомиться с математическим аппаратом, применяемым для описания свойств векторных полей. Этот аппарат называется векторным анализом. В данном параграфе мы рассмотрим основные понятия и некоторые формулы векторного анализа, а также докажем две главные теоремы векторного анализа: теорему Остроградского — Гаусса и теорему Стокса.

Наибольшую наглядность величины, используемые в векторном анализе, имеют в случае поля вектора скорости текущей жидкости. Поэтому мы будем вводить эти величины, рассматривая течение идеальной несжимаемой жидкости, а затем распространять полученные результаты на векторные поля любой природы.

С одним из понятий векторного анализа мы уже знакомы. Это — градиент, используемый для характеристики скалярных полей. Если каждой точке Р с координатами х, у, z сопоставляется значение скалярной величины , говорят, что задано скалярное поле . Градиентом величины 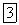 называется вектор

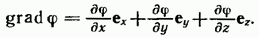
Приращение функции  при смещении на отрезок 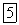 равно

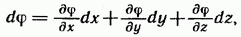
что можно представить в виде

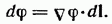
Теперь перейдем к установлению характеристик векторных полей.

Поток вектора.

Пусть течение жидкости охарактеризовано полем вектора скорости. Объем жидкости, протекающей в единицу времени через некоторую воображаемую поверхность S, называется потоком жидкости через эту поверхность. Чтобы найти поток, разобьем поверхность на элементарные участки величины . Из рис. 11.1 видно, что за время  через участок  пройдет объем жидкости, равный

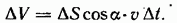
Разделив этот объем на промежуток времени  найдем поток через поверхность 

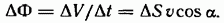
Перейдя к дифференциалам, получим, что

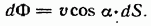
Формулу (11.3) можно написать еще двумя способами. Во-первых, если учесть, что  дает проекцию вектора скорости на нормаль  к площадке  можно представить (11.3) в виде

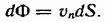
Во-вторых, можно ввести вектор  модуль которого равен величине площадки  а направление совпадает с направлением нормали к площадке :

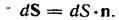
Поскольку выбор направления вектора  условен (его можно направить как в одну сторону от площадки, так и в другую),  является не истинным вектором, а псевдовектором. Угол а в формуле (11.3) есть угол между векторами v и dS. Следовательно, эту формулу можно написать в виде

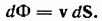
Просуммировав потоки через все элементарные площадки, на которые мы разбили поверхность , получим поток жидкости через S:

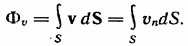
Аналогичное выражение, написанное для произвольного векторного поля а, т. е. величина

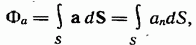
называется потоком вектора а через поверхность S.

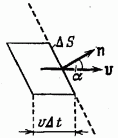
Рис. 11.1.

В соответствии с этим определением поток жидкости может быть назван потоком вектора v через соответствующую поверхность (см. (11.6)).

Поток вектора есть алгебраическая величина, причем знак его зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении потока. Изменение направления нормали на противоположное изменяет знак у  а следовательно, и знак величины (11.7). В случа замкнутых поверхностей принято вычислять поток, «вытекающий» из охватываемой поверхностью области наружу. Соответственнс в качестве  в дальнейшем будет всегда подразумеваться обращенная наружу (т. е. внешняя) нормаль.

Потоку вектора можно дать наглядную геометрическую интерпретацию. Для этого представим векторное поле системой линий а, построенных так, чтобы густота линий в каждом месте была численно равна модулю вектора а в той же точке поля (ср. с правилом построения линий вектора Е, изложенным в конце § 5). Найдем число  пересечений линий поля с воображаемой площадкой . Из рис. 11.2 видно, что это число равно густоте линий (т. е. а), умноженной на 

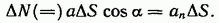
Речь идет лишь о числовом равенстве между  и  Поэтому знак равенства заключен в скобки. Согласно (11.7) выражение  представляет собой  — поток вектора а через площадку . Таким образом,

Для того чтобы знак  совпал со знаком  нужно пересечения, при которых угол а между положительным направлением линии поля и нормалью к площадке является острым, считать положительными. В случае же, если угол а тупой, пересечение нужно считать отрицательным. Для изображенной на рис. 11.2 площадки все три пересечения являются положительными:  в этом случае также положителен, поскольку  Если направление нормали на рис. 11.2 изменить на обратное, пересечения станут отрицательными  поток  также будет отрицательным.

Просуммировав выражение (11.8) по конечной воображаемой поверхности S, получим соотношение

где под  подразумевается полное число положительных пересечений линий поля с поверхностью S, а под N_ — полное число отрицательных пересечений.

Может вызвать недоумение то обстоятельство, что, поскольку поток, как правило, выражается нецелым числом, сопоставляемое потоку число пересечений линий поля с поверхностью также будет нецелым. Однако смущаться этим не следует. Линии поля представляют собой чисто условный образ, никакого физического смысла они не имеют.

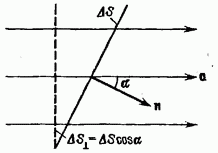
Рис. 11.2.

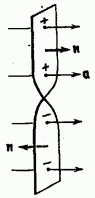
Рис. 11.3.

Возьмем воображаемую поверхность в виде полоски бумаги, нижняя часть которой закручена относительно верхней на угол  (рис. 11.3). Выбор направления нормали для всей поверхности должен быть сделан одинаковым образом. Поэтому, если в верхней части полоски положительную нормаль направить вправо, то в нижней части нормаль будет направлена влево. Соответственно пересечения изображенных на рис. 11.3 линий поля с верхней половиной поверхности нужно считать положительными, а с нижней половиной — отрицательными.

Для замкнутой поверхности (рис. 11.4) положительной считается внешняя нормаль. Поэтому пересечения, соответствующие выходу линий наружу (в этом случае угол а острый), нужно брать со знаком плюс, а пересечения, возникающие при входе линий внутрь (в этом случае угол а тупой), надо брать со знаком минус.

Из рис. 11.4 видно, что в случае, когда линии поля проходят внутри замкнутой поверхности непрерывно, каждая линия, пересекая поверхность, входит внутрь и выходит наружу одинаковое число раз. В итоге поток соответствующего вектора через эту поверхность оказывается равным нулю. Легко сообразить, чтов случае, если линии поля обрываются внутри поверхности, поток вектора через замкнутую поверхность будет численно равен разности числа линий, начинающихся внутри поверхности  и числа линий, оканчивающихся внутри поверхности ():

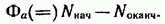
Знак потока зависит от того, какое из этих чисел больше. При  поток равен нулю.