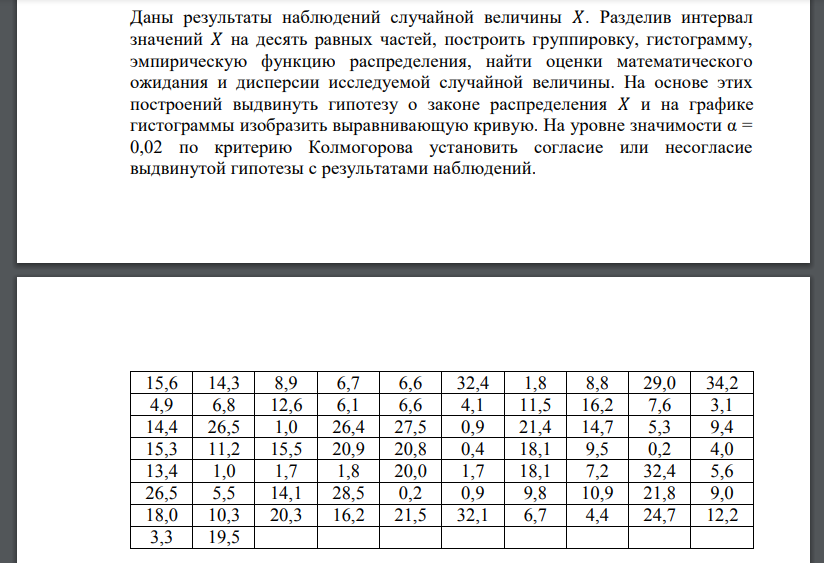
Даны результаты наблюдений случайной величины 𝑋. Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16394
		Прошла проверку преподавателем МГУ
		245 руб.

Даны результаты наблюдений случайной величины 𝑋. Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, найти оценки математического ожидания и дисперсии исследуемой случайной величины. На основе этих построений выдвинуть гипотезу о законе распределения 𝑋 и на графике гистограммы изобразить выравнивающую кривую. На уровне значимости α = 0,02 по критерию Колмогорова установить согласие или несогласие выдвинутой гипотезы с результатами наблюдений. 

Решение

Построим вариационный ряд – выборку в порядке возрастания:  Объем данной выборки (то есть число объектов в выборке) равен 𝑛 = 72. Найдем размах выборки Разделим весь полученный диапазон наблюдаемых значений на 10 равных частей. Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Распределим компоненты выборки по десяти разрядам длины Построим группировку. В таблице приняты следующие обозначения: 𝑚𝑗 – частота разряда ∆𝑗 , то есть количество вариант выборки, попавших в j−й разряд; 𝑧𝑗 ∗ – середины разрядов; 𝑚𝑗 ∗ – накопленные частоты разрядов. Величины 𝜋𝑗 ∗ называются накопленными частостями разрядов и используются для построения эмпирической функции распределения. На основе проведенных вычислений строим гистограмму и эмпирическую функцию распределения. Далее найдем оценки математического ожидания и дисперсии исследуемой случайной величины. В качестве оценки математического ожидания возьмем выборочное среднее  в качестве оценки дисперсии – выборочную дисперсию:  Все промежуточные вычисления удобно заносить в таблицу: Построим далее выравнивающую кривую гистограммы. Исходя из вида гистограммы и графика эмпирической функции, можно предположить, что неизвестное распределение случайной величины 𝑋 подчиняется показательному закону с некоторым неизвестным параметром 𝜆. В качестве оценки 𝜆 можно принять величину 1 𝑀𝑛 , тогда теоретическая плотность распределения будет иметь вид: Строим график функции  при выбранном параметре 𝜆 и накладываем его на гистограмму, получаем выравнивающую кривую гистограммы: Проверим в условиях данной задачи с помощью критерия Колмогорова при условии значимости α=0.02 гипотезу о том, что случайная величина 𝑋 распределена по показательному закону с параметром  Для этого вычислим статистику Колмогорова по формуле  где 𝐹𝑛 − эмпирическая функция распределения, − теоретическая функция распределения. Откуда получаем  Найдем критическое значение статистики Колмогорова при уровне значимости По таблице значений функции Колмогорова находим  из условия  откуда  следовательно,  Так как  то выдвинутую гипотезу принимаем.