Исследовался средний месячный доход (тыс. руб.) жителя определённого региона по выборке из 1000 жителей. Полученный результат

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16394
		Прошла проверку преподавателем МГУ
		245 руб.

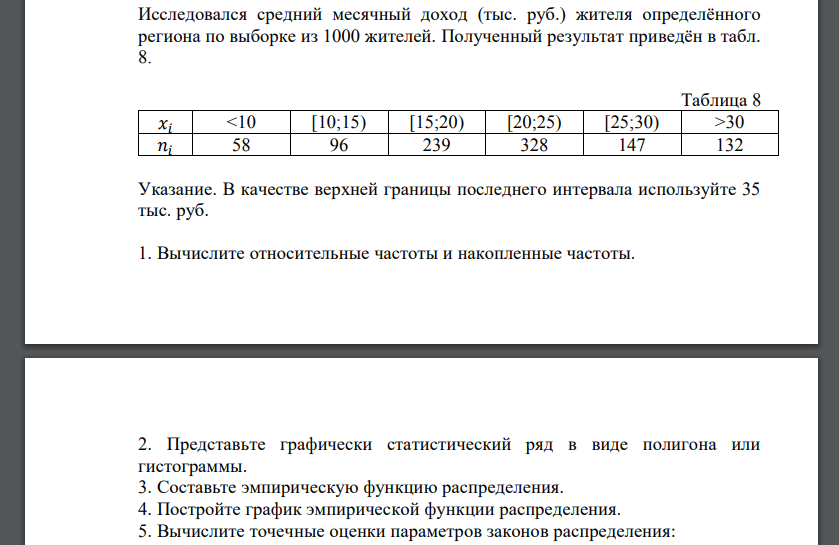
Исследовался средний месячный доход (тыс. руб.) жителя определённого региона по выборке из 1000 жителей. Полученный результат приведён в табл. 8. Таблица 8 𝑥𝑖 30 𝑛𝑖 58 96 239 328 147 132 Указание. В качестве верхней границы последнего интервала используйте 35 тыс. руб. 1. Вычислите относительные частоты и накопленные частоты. 2. Представьте графически статистический ряд в виде полигона или гистограммы. 3. Составьте эмпирическую функцию распределения. 4. Постройте график эмпирической функции распределения. 5. Вычислите точечные оценки параметров законов распределения: 1) выборочное среднее; 2) выборочную смещённую (неисправленную) дисперсию и выборочную несмещённую (исправленную) дисперсию; 3) выборочное неисправленное среднее квадратическое отклонение и выборочные исправленное среднее квадратическое отклонение; 4) выборочную моду; 5) выборочную медиану. 6. Найдите доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при условии, что дисперсия неизвестна, если доверительная вероятность задана как 𝛾 = 0,9 + 0,01𝑖 , где 𝑖 – последняя цифра шифра зачётной книжки.

Решение

1. Вычислим относительные частоты и накопленные частоты. Относительную частоту для каждого интервала 𝜔𝑖 найдем по формуле:  Накопленные частоты 𝜔 так же внесем в таблицу. . Представим графически статистический ряд в виде гистограммы относительных частот. 3. Составим эмпирическую функцию распределения. Эмпирическая функция распределения выглядит следующим образом . Построим график эмпирической функции распределения. 5. Вычислим точечные оценки параметров законов распределения: 1) выборочное среднее;  2) выборочную смещённую 𝐷в (неисправленную) дисперсию и выборочную несмещённую 𝑆 2 (исправленную) дисперсию;  3) выборочное неисправленное 𝜎в среднее квадратическое отклонение и выборочные исправленное 𝑆 среднее квадратическое отклонение;  4) Мода – это наиболее часто повторяющееся значение признака, определяется по формуле:  – нижнее значение модального интервала; 𝑓𝑀𝑜 – частота в модальном интервале; 𝑓𝑀𝑜−1 – частота в предыдущем интервале; 𝑓𝑀𝑜+1 – частота в следующем интервале за модальным; ℎ – размах интервала. Модальный интервал – это интервал с наибольшей частотой, т.е. в данном случае 20 – 25. Тогда 5) Рассчитаем медиану:  где 𝑋0 – нижняя граница интервала, в котором находится медиана; ℎ – размах интервала; 𝑓′𝑀𝑒−1 – накопленная частота в интервале, предшествующем медианному; 𝑓𝑀𝑒 – частота в медианном интервале. Медианный интервал – это тот, на который приходится середина ранжированного ряда, т.е. в данном случае . Найдем доверительный интервал для неизвестного математического ожидания нормально распределённой генеральной совокупности при условии, что дисперсия неизвестна, если доверительная вероятность 𝛾 = 0,98. Доверительный интервал для математического ожидания a случайной величины равен:  где 𝑡 – такое значение аргумента функции Лапласа, при котором . По таблице функции Лапласа находим t из равенства:  Получаем 𝑡 = 2,33 и искомый доверительный интервал имеет вид: