Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.

Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Математическая статистика
Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Решение задачи
Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.
Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Выполнен, номер заказа №16444
Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Прошла проверку преподавателем МГУ
Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌. Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.  245 руб. 

Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид:

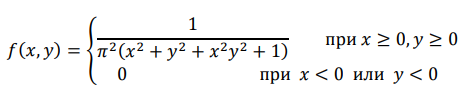
Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.

1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.

Решение

Преобразуем заданную функцию: Совместная функция распределения имеет вид: ) Случайные величины 𝑋 и 𝑌 называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид:  Определим законы распределения одномерных величин 𝑋 и 𝑌. Для плотности распределения величины  Для плотности распределения величины  Для данного случая: Поскольку равенство верно, то величины 𝑋 и 𝑌 являются независимыми.

Плотность распределения двумерно случайной величины (𝑋, 𝑌) имеет вид: 1) Найти функцию распределения 𝐹(𝑥, 𝑦); 2) Установить, зависимы ли 𝑋, 𝑌.

Похожие готовые решения по математической статистике: