По данной выборке: Найти относительные частоты и построить полигон частот. 2. Построить эмпирическую функцию распределения. 3. Найти

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16393
		Прошла проверку преподавателем МГУ
		245 руб.

По данной выборке: Найти относительные частоты и построить полигон частот. 2. Построить эмпирическую функцию распределения. 3. Найти несмещенные оценки генеральной средней и генеральной дисперсии. 4. Методом моментов найти точечные оценки параметров нормально распределенной генеральной совокупности. 5. Построить доверительные интервалы надежности для оценки параметров  нормально распределенной генеральной совокупности. 6. При уровне значимости проверить гипотезы о числовых значениях параметров: 

Решение

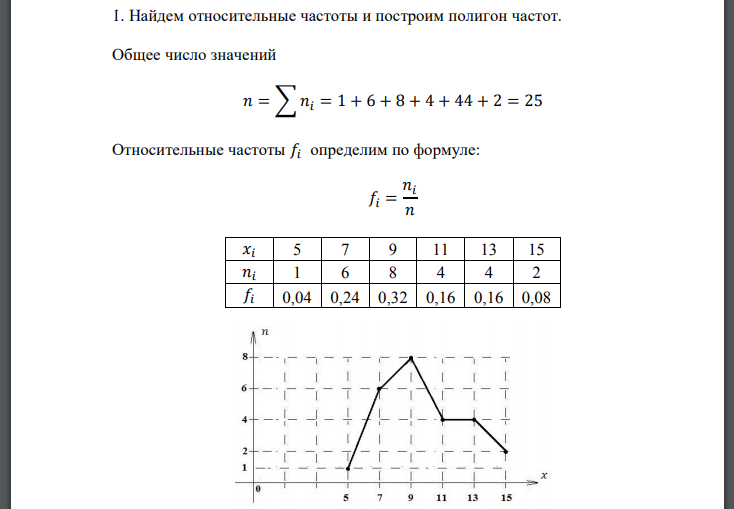
1. Найдем относительные частоты и построим полигон частот. Общее число значений Относительные частоты  определим по формуле: Построим эмпирическую функцию распределения. Найдем несмещенные оценки генеральной средней (выборочное среднее и генеральной дисперсии (исправленную выборочную дисперсию 4. Методом моментов найдем точечные оценки параметров нормально распределенной генеральной совокупности. Параметр  нормально распределенной генеральной совокупности равен начальному моменту первого прядка: Параметр нормально распределенной генеральной совокупности равен центральному моменту второго прядка: Построим доверительные интервалы надежности 𝛾 = 0,95 для оценки параметров нормально распределенной генеральной совокупности. Доверительный интервал для математического ожидания a нормально распределенной случайной величины равен: где – такое значение аргумента функции Лапласа, при котором По таблице функции Лапласа находим из равенства: Получаем и искомый доверительный интервал имеет вид: Найдем доверительный интервал для генеральной дисперсии по формуле:  При получим: Тогда  При уровне значимостипроверим гипотезы о числовых значениях параметров. Для проверки нулевой гипотезы применим статистику: Поскольку конкурирующая гипотеза имеет вид критическая область является двусторонней. При уровне значимости и числу степеней свободы по таблице критических точек распределения Стьюдента находим:  Так как то нулевую гипотезу принимаем. Для проверки нулевой гипотезы применим статистику:  Поскольку конкурирующая гипотеза имеет вид критическая область является правосторонней. При уровне значимости и числу степеней свободы по таблице распределения Пирсона находим:  Так как то нулевую гипотезу принимаем