Проведено обследование времени, которое транспорт простаивает в пробках в течение дня, для чего из 1000 городских автобусов

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16472
		Прошла проверку преподавателем МГУ
		245 руб.

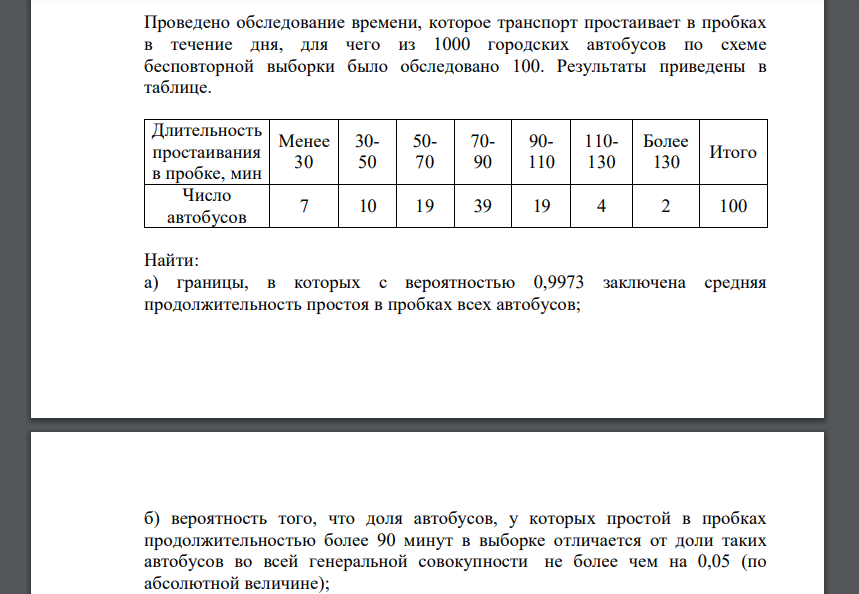
Проведено обследование времени, которое транспорт простаивает в пробках в течение дня, для чего из 1000 городских автобусов по схеме бесповторной выборки было обследовано 100. Результаты приведены в таблице. Длительность простаивания в пробке, мин Менее 30 30- 50 50- 70 70- 90 90- 110 110- 130 Более 130 Итого Число автобусов 7 10 19 39 19 4 2 100 Найти: а) границы, в которых с вероятностью 0,9973 заключена средняя продолжительность простоя в пробках всех автобусов; б) вероятность того, что доля автобусов, у которых простой в пробках продолжительностью более 90 минут в выборке отличается от доли таких автобусов во всей генеральной совокупности не более чем на 0,05 (по абсолютной величине); в) объем повторной выборки, при котором с вероятностью 0,95 можно гарантировать то же отклонение доли, что и в пункте б). Решение

а) Найдем выборочное среднее  Выборочная дисперсия:  Исправленная выборочная дисперсия:  Исправленное среднеквадратичное отклонение Доверительный интервал для математического ожидания 𝑎 случайной величины равен:  где t – такое значение аргумента функции Лапласа, при котором Ф(𝑡) = 1 2 𝛾. По таблице функции Лапласа находим 𝑡 из равенства:   Получаем 𝑡 = 3 и искомые границы, в которых с вероятностью 0,9973 заключена средняя продолжительность простоя в пробках всех автобусов, имеют вид: б) Найдем вероятность того, что доля автобусов, у которых простой в пробках продолжительностью более 90 минут в выборке отличается от доли таких автобусов во всей генеральной совокупности не более чем на 0,05 (по абсолютной величине). При заданных условиях  . Выборочная доля автобусов, у которых простой в пробках продолжительностью более 90 минут, равна: