
Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная величина
 |
 |
Математическая статистика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16457 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная величина, эмпирические данные которой даны в таблице, обладает нормальным законом распределения. За значение параметра 𝑎 и 𝜎 принять среднюю выборочную и выборочную дисперсию, вычисленные по эмпирическим данным.
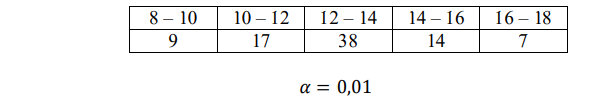
Решение
Общее число значений Выборочное среднее вычисляется по формуле: Выборочная дисперсия вычисляется по формуле: Проверим с помощью критерия Пирсона гипотезу о нормальном распределении. Принимая найдем вероятность попадания случайной величины в каждый интервал: Теоретические частоты определим по формуле и вычислим значения Результаты запишем в таблицу Интервал Получили Число степеней свободы По таблице при уровне значимости находим Так как то нет основания отвергать гипотезу о нормальном распределении. Проверим выдвинутую гипотезу о законе распределения случайной величины с помощью критерия согласия Колмогорова при уровне значимости В таблицу запишем значения функции распределения и для всех значений 𝑥 (правые границы соответствующих интервалов) рассчитаем значения: Из таблицы вероятностей Колмогорова выберем критическое значение Значение критерия Колмогорова: Поскольку то гипотеза о нормальном законе распределения согласуется с опытными данными. Проверим с помощью критерия Мизеса гипотезу о нормальном распределении. В таблицу запишем значения функции распределения нормального закона, значения эмпирической функции распределения и средний квадрат отклонения Из таблице критерия Мизеса выберем критическое значение Найденное значение критерия Мизеса: Поскольку то гипотеза о нормальном законе распределения согласуется с опытными данными.

Похожие готовые решения по математической статистике:
- Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная величина, эмпирические
- Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная
- Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная величина, эмпирические данные
- Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная величина, эмпирические данные которой
- При исследовании партии картофеля было проведено 𝑛 проб и полученные данные о содержании крахмала в клубнях в 𝑥% приведены в таблице
- При исследовании партии картофеля было проведено n проб и полученные данные о содержании крахмала в клубнях в x% приведены
- В таблице приведены результаты 2608 опытов по наблюдению 𝛼 −частиц, излучаемых данным радиоактивным веществом за определенный
- Задание №3. Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная
- Функция рыночного спроса на товар и функция общих издержек монопольного продавца товара заданы формулами: x=x(p), C=C(x). 1. Постройте кривую рыночного спроса. 2. Вычислите ценовую эластичность
- Задание №3. Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная
- Проверить с помощью критерия Пирсона, Колмогорова и Мизеса при заданном уровне значимости 𝛼 гипотезу о том, что случайная величина, эмпирические
- Процесс выращивания пшеницы в некотором хозяйстве описывается ПФ q = 2( x1x2 x1 2 x2 2 ), где: x1 – число сотен отработанных человеко-часов, x2 – число обработанных акров земли [акр(acre) – единица площади в английской

