
Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.
Средняя длина детали составляет 50 см, а дисперсия равна 0,1. Оценить вероятность того, что изготовленная деталь окажется по длине
 |
 |
Теория вероятностей |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16360 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Описание заказа и 38% решения ( + фото):
Средняя длина детали составляет 50 см, а дисперсия равна 0,1. Оценить вероятность того, что изготовленная деталь окажется по длине не меньше 40,5 см и не больше 50,5 см.
Решение
Для нормального закона распределения случайной величины вероятность попадания в заданный интервал равна: Ответ:

Похожие готовые решения по теории вероятности:
- Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно 𝑀𝑥 = 12, дисперсия
- Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно 𝑀𝑥 = 42, дисперсия
- Случайная величина «размер детали» имеет нормальное распределение с известными 𝑀𝑋 = 23,96379 и 𝐷𝑋 = 1,274112. Поле допуска
- Случайная величина Х распределена по нормальному закону с математическим ожиданием 40 и дисперсией
- Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 30 и дисперсией 100. Найти вероятность
- Вес выловленных в пруду рыб распределяется по нормальному закону со средним значением 300 г и дисперсией
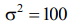 . Найти вероятность того
. Найти вероятность того - СВ 𝑋 распределена с 𝑀(𝑥) = 2,8, 𝐷(𝑥) = 0,36. Найти вероятность попадания СВ 𝑋 в интервал
- Случайная величина 𝑋 распределена по нормальному закону с математическим ожиданием 30 и дисперсией 100. Вычислить
- Для проверки качества сплава, из которого изготавливают сверла, была измерена величина износа
- Случайная величина 𝑋 распределена по нормальному закону с математическим ожиданием 30 и дисперсией 100. Вычислить
- Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно 𝑀𝑥 = 12, дисперсия
- В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется: а) записать значения результат

