
В ABCD случайным образом бросаются точки. Найти мат.ожидание, дисперсию и медиану X.
 |
 |
Математическая статистика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16444 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
В ABCD случайным образом бросаются точки. Найти мат.ожидание, дисперсию и медиану X.
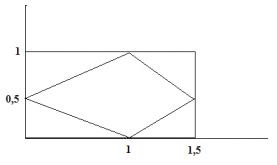
Решение
Границы области Плотность распределения равна: остальные (𝑥; 𝑦) Определим константу 𝑐, используя условие нормировки Тогда Найдем математическое ожидание Найдем дисперсию Графически прямая х = Ме (где Ме – искомая медиаена) делит площадь фигуры, ограниченной кривой распределения, на две равные части. Найдем площадь ABCD из простых формул геометрии: 𝑆Половина этой площади равна 𝑆1 = 3 8 Площадь двух больших треугольников равна 1 2 , что больше 3 8 , значит медиана левее прямой

Похожие готовые решения по математической статистике:
- Функция распределения непрерывного случайного вектора 𝐹(𝑥, 𝑦) = { 𝑠𝑖𝑛𝑥 ∙ 𝑠𝑖𝑛𝑦, 𝑥 ∈ [0; 𝜋 2 ], 𝑦 ∈ [0; 𝜋 2 ] 0 𝑥 < 0, 𝑦 < 0 1 𝑥 > 𝜋 2 , 𝑦 > 𝜋 2 Найти плотность
- Плотность распределения непрерывного случайного вектора 𝑓(𝑥; 𝑦) = { 1 2 𝑠𝑖𝑛(𝑥 + 𝑦), 𝑥 ∈ [0; 𝜋 2 ], 𝑦 ∈ [0; 𝜋 2 ] 0, остальные (𝑥; 𝑦) Найти плотности компонент
- Система случайных величин (𝑥, 𝑦) имеет плотность вероятности: Требуется: 1) найти коэффициент 𝑎; 2) найти вероятность попадания в
- В первом квадранте задана двумерная плотность распределения вероятности системы двух СВ: 𝑝(𝑥; 𝑦) = 𝑙𝑛22 ∙ 2 −𝑥−𝑦 ; вне квадранта 𝑝(𝑥; 𝑦) = 0. Найти
- Двумерная случайная величина (𝑋; 𝑌) имеет равномерное распределение плотности вероятности в треугольной области 𝐴𝐵𝐶, заданной функцией 𝑓(𝑥; 𝑦).
- Дана двумерная плотность вероятности: Найдите 𝑐 и плотность вероятности СВ 𝑋, 𝑌. Являются ли они зависимыми или независимыми?
- Задана плотность совместного распределения двумерной случайной величины (𝑋, 𝑌): 𝑓(𝑥; 𝑦) = { 𝑐(2𝑥 + 𝑥𝑦 2 ) 1 ≤ 𝑥 ≤ 2, 0 ≤ 𝑦 ≤ 2 0 иначе Определить:
- Задана плотность совместного распределения двумерной случайной величины (𝑋, 𝑌): 𝑓(𝑥; 𝑦) = { 36𝑥𝑦𝑒 −3(𝑥 2+𝑦 2) (𝑥 > 0, 𝑦 > 0) 0 (𝑥 < 0, или 𝑦 > 0) Найти
- В студенческой группе 3 девушки и 4 юноши. По списку наугад выбираются 4 обучающихся. Какова вероятность того, что среди них окажутся 3 юношей?
- В аудитории 14 студентов, 5 из которых юноши. Известно, что к доске должны вызвать 3 студентов. Какова вероятность, что среди вызванных
- Студент знает 20 вопросов из 35 вопросов программы. Экзаменатор задает три вопроса из имеющихся. Найти вероятность того, что студент знает
- В студенческой группе 7 девушек и 8 юношей. Тогда вероятность того, что на конференцию пойдут 2 девушки и 1 юноша, равна…

