Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа

В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа Математическая статистика
В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа Решение задачи
В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа
В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа Выполнен, номер заказа №16457
В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа Прошла проверку преподавателем МГУ
В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа  245 руб. 

В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа стандартных деталей среди 3 отобранных. Найти: а) функцию распределения 𝐹(𝑥) случайной величины 𝑋 и построить ее график; б) 𝑀(𝑍), 𝐷(𝑍) и 𝜎(𝑍), где 𝑍 = 2𝑋 − 8𝑌 и случайная величина 𝑌 имеет вид:

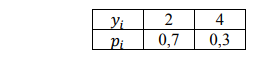
В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа

Решение

Случайная величина 𝑋 – число стандартных деталей среди отобранных, может принимать значения  По классическому определению вероятности, вероятность события 𝐴 равна  где 𝑚 – число благоприятных исходов, 𝑛 – общее число исходов. Число возможных способов выбрать 3 детали из 15 равно:  Благоприятствующими являются случаи, когда из общего числа 10 стандартных деталей выбрали 0,1,2,3 и из общего числа 5 нестандартных деталей выбрали 3,2,1,0 соответственно. Закон распределения имеет вид: а) Функция распределения выглядит следующим образом: б) Найдем математические ожидания 𝑀(𝑋) и 𝑀(𝑌) а также дисперсии 𝐷(𝑋) и 𝐷(𝑌) для случайных величин 𝑋 и 𝑌. По свойствам математического ожидания По свойствам дисперсии  Среднее квадратическое отклонение для случайной величины 𝑍 равно:

В партии из 15 деталей содержатся 5 нестандартных. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины 𝑋 – числа

Похожие готовые решения по математической статистике: