
Выборочная зависимость между величиной основных производственных фондов и суточной выработкой продукции по данным пяти независимых наблюдений представлена в таблице.
 |
 |
Экономическая теория |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №17599 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Выборочная зависимость между величиной основных производственных фондов и суточной выработкой продукции по данным пяти независимых наблюдений представлена в таблице. Требуется составить выборочное уравнение линейной парной регрессии вычислить коэффициент корреляции между на уровне значимости проверить значимость коэффициента корреляции и уравнения регрессии.
РЕШЕНИЕ
Составим расчетную таблицу задачи: Выборочное уравнение линейной регрессии имеет вид: Параметры уравнения находятся из системы нормальных уравнений: объем выборки. Согласно данным расчетной таблицы имеем: Решение этой системы может быть получено любым из известных методов или вычислено по формулам: где Значения указаны в расчетной таблице: Поэтому находим: Следовательно, искомое уравнение регрессии имеет вид: Из полученного уравнения регрессии следует, что при увеличении основных производственных фондов на одну денежную единицу, суточная выработка продукции предприятия увеличится в среднем на 1,096 (условных единиц). Найдем коэффициент корреляции r между определяемый по формуле , выборочные дисперсии переменных х и у соответственно. Согласно данным расчетной таблицы имеем: и, следовательно, Теперь находим: Очевидно, что связь между рассматриваемыми переменными достаточно тесная. Проверим значимость коэффициента корреляции между Статистика критерия значимости определяется формулой , объем выборки. Вычислим ее значение: Выборочное значение коэффициента корреляции значимо отличается от нуля, если табличное значение критерия Стьюдента, определенное на уровне значимости α при числе степеней свободы Для заданного уровня значимости α=0,05 и числе степеней свободы находим по таблицам критическое значение статистики: Поскольку то коэффициент корреляции между суточной выработкой продукции У и величиной основных производственных фондов значимо отличается от нуля и между переменными действительно существует корреляционная зависимость. Оценим значимость уравнения регрессии. В случае линейной парной регрессии уравнения значимо, если для значения критерия Фишера-Снедекора выполняется неравенство Вычислим значение По таблице распределения находим значение при заданном уровне значимости Имеем Так как то уравнение регрессии значимо.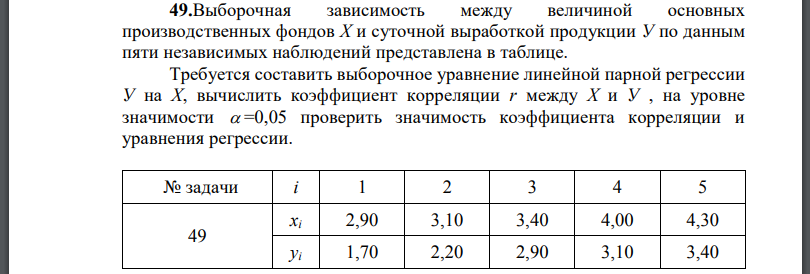

Похожие готовые решения по экономической теории:
- Имеются данные (условные) о сменной добыче угля и уровне механизации работ характеризующие процесс добычи угля в семи шахтах.
- В таблице приведены данные, отражающие спрос на некоторый товар за семилетний период (усл. ед.). Найти уравнение тренда для временного ряда
- Выборка случайной величины Х задана интервальным вариационным рядом интервал, частота). Найти: относительные частоты (частости)
- Ежемесячный объем выпуска продукции завода является случайной величиной, распределенной по показательному закону. Имеются данные
- Выборка случайной величины Х задана интервальным вариационным рядом интервал, частота). Найти: относительные частоты (частости) накопленные
- Ежемесячный объем выпуска продукции завода является случайной величиной, распределенной по показательному закону. Имеются данные
- Для проверки эффективности новой технологии отобраны две группы рабочих численностью человек. В первой группе, где применялась новая технология, выборочная
- Для проверки влияния технологии на качество однотипной продукции проведена выборочная проверка процента брака за пять месяцев на трех производственных участках.
- Получить канонические уравнения четырёх кривых второго порядка, заданных уравнениями
- Количество изделий, шт. Количество рабочих 10 11 12 13 14 15 16 17 18 7 3 15 10 12 4 13 9 2 Определить: 1. Среднюю выработку. 2. Моду. 3. Медиану
- Отдел технического контроля проверил партий однотипных изделий и установил, что число Х нестандартных изделий в одной партии
- Построить полигон частот, найти выборочную среднюю и выборочную дисперсию по данному распределению выборки

