Задан сгруппированный вариационный ряд (в первой строке – возможные значения случайной величины, во второй строке – число таких

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16457
		Прошла проверку преподавателем МГУ
		245 руб.

Задан сгруппированный вариационный ряд (в первой строке – возможные значения случайной величины, во второй строке – число таких значений в выборке):

Построить гистограмму и эмпирическую функцию распределения вероятностей. 2. Определить моду. 3. Построить доверительный интервал для истинного значения измеряемой величины с доверительной вероятностью 0,92, если среднее квадратическое отклонение 𝜎_𝑥 = 0,2. 4. Сколько раз нужно было измерить эту постоянную величину, чтобы с вероятностью не меньшей чем 0,94 можно было утверждать, что эмпирическое математическое ожидание отклоняется от истинного математического ожидания на величину не большую, чем 0,4? 5. Пусть средняя квадратическая ошибка прибора является неизвестной. Требуется построить доверительный интервал для измеряемой величины при уровне значимости 0,001.

Решение

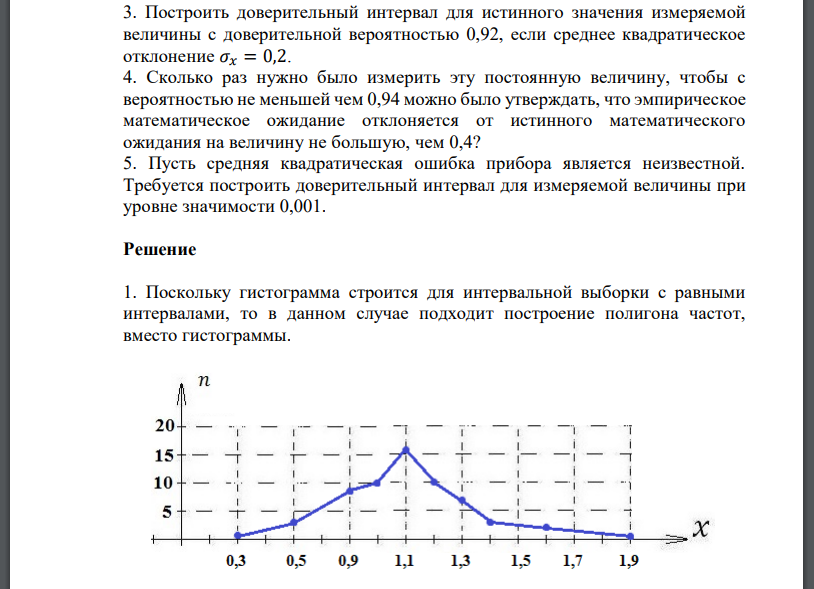
1. Поскольку гистограмма строится для интервальной выборки с равными интервалами, то в данном случае подходит построение полигона частот, вместо гистограммы. Относительные частоты (частости) определим по формуле:  – общее число значений.Эмпирическая функция распределения выглядит следующим образом: 2. Поскольку наибольшая вероятность достигается при значении, то мода равна:  Выборочное среднее значение равно: Доверительный интервал для истинного значения измеряемой величины равен:  где 𝑡 – такое значение аргумента функции Лапласа, при котором По таблице функции Лапласа находим 𝑡 из равенства: Получаем и искомый доверительный интервал имеет вид:  По условию отклонение не должно превышать 0,4, с вероятностью не меньшей чем 0,94. При этом 𝑡 – такое значение аргумента функции Лапласа, при котором По таблице функции Лапласа находим 𝑡 из равенства:  Получаем Тогда Полученное значение даже не превосходит единицы, что говорит об неудачно подобранном значении 0,4 (оно слишком велико, найденный интервал для вероятности 0,92 описывается границами ±0,045). 5. Пусть средняя квадратическая ошибка прибора является неизвестной. Выборочная дисперсия равна: Несмещенная (исправленная) оценка генеральной дисперсии Доверительный интервал для истинного значения измеряемой величины равен: где 𝑡 – такое значение аргумента функции Лапласа, при котором По таблице функции Лапласа находим 𝑡 из равенства: Получаем и искомый доверительный интервал имеет вид: