Расчет сложных электрических цепей переменного синусоидального тока

Содержание:

Введение

Зарождение науки об электричестве относится к XVI в., когда английский ученый У. Гильберт (1544-1603) написал свой знаменитый трактат «О магните, проведены многочисленные опыты, позволившие установить существование электрических зарядов двух типов – положительных и отрицательных, изобрести первый конденсатор (Ж. Нолпе, 1745), разработать первую последовательную теорию электрических явлений (Б. Франклин).

    Во второй половине XVIII в. началось «количественное изучение» электрических и магнитных явлений, появились измерительные приборы – электроскопы. В 1756 г. петербургский физик Ф. Эпинус (1724 – 1802) изобрел воздушный конденсатор, с помощью которого показал, что стекло в «лейденской» банке обладает свойством накапливать электричество, открыл явление электризации некоторых тел (турмалин) при нагревании (пироэлектричество). В работе Ф. Эпинуса впервые предпринята систематическая попытка подойти к изучению электрических явлений не только с качественной, но с количественной стороны. В частности, им было установлено, что сила взаимодействия между зарядами пропорциональна величине этих зарядов. И хотя он не установил, как эта сила зависит от расстояния, однако, значение его работы очень велико, так как она дала определенное направление дальнейшим исследованиям. Наконец, в 1784 г. французский 48-летний военный инженер Ш. Кулон (1736-1806) открывает закон, согласно которого сила взаимодействия между электрическими зарядами обратно пропорциональна квадрату расстояния между ними. С помощью созданных им крутильных весов, и также ряда оригинальных методов (методы колебаний) этот человек, никогда специально не занимавшийся электричеством и магнетизмом, проводя в качестве побочного занятия свои исследования. Заложил основы количественной электростатики.

    Законы Ома (1826 г.). Законы Кирхгофа (1847 г.). Открытие И. Фарадеем (1831 г.) явления электромагнитной индукции. Русский ученый (Э. Ленц) в (1833 г.) открыл закон, установивший связь между направлением индукционных токов и их электромагнитными взаимодействиями. Таким образом, к концу 19 в. было установлено единство электромагнитных явлений, получившее свое завершение в работах Дж. Максвелла. В конце 19 в. – начале 20 в. открыт дискретный характер зарядов (Дж. Томсон, 1897 г.) – начался новый этап в развитии науки об электричестве. Со второй половины XIX в. началось широкое использование электрических и магнитных явлений в технике:

 - электродвигатели;

 - генераторы тока;

- освещение (изобретение эл. связи Яблочковым)

- электротехнологии (Б.С. Якоби в 1893 г.) он предложил использовать электрический ток для нанесения металлических покрытий.

    Русский инженер Доливо-Добровольский к концу 90-х г.г. 19 в. разработал трехфазные асинхронные электрические двигатели. Он построил 3-х фазную линию электропередач на 175 км.

    Современная энергетика – это ключевая отрасль экономики страны. Она играет определенную роль в развитии научно-технического прогресса, интенсификации производства любой отрасли. Во всех областях деятельности современного общества применяется электрическая энергия. Ряд ее замечательных свойств обеспечивают преимущества над другими видами энергии:

1. Относительная простота получения за счет преобразования из других видов энергии (механической, химической, тепловой, световой, атомной).

2. Простота передачи энергии с высоким КПД на большие расстояния и распределение ее между потребителями.

3. Совершенство потребления к одному источнику самой различной мощности.

4. Простота изменения параметров (напряжения и тока).

5. Возможность практически мгновенной передачи сигналов на большие расстояния (телефония, телеграфия, радиотехника).

Эти свойства электрической энергии позволили в очень короткий исторический срок не только решить основные вопросы самой электроэнергетики, но и модернизировать «неэлектрическую технику», перевести ее на качественно новый уровень. На базе электротехнической науки начали развиваться электроника, радиотехника, производство различных электротехнических устройств, в том числе вычислительная техника. Возникновение электротехники относится к периоду создания источника постоянного тока (начало 19 в.) и последовавших затем открытий в области электричества и магнетизма.

Исходные данные и рассчитываемая схема

Таблица 1. Исходные данные

Параметр

E1, [B]

ψe1, [град]

E4, [B]

ψe4, [град]

E5, [B]

ψe5, [град]

E7, [B]

ψe7, [град]

E8, [B]

Значение

9

54

30

-95

27

119

7

-5

13

Параметр

ψe8, [град]

E10, [В]

ψe10, [град]

J2, [А]

ψi2, [град]

J3, [А]

ψi3, [град]

J4, [А]

ψi4, [град]

f, [Гц]

Значение

-45

14

34

12

62

25

15

1

-70

50

Параметр

Z1, [Ом]

Z3, [Ом]

Z6, [Ом]

Z7, [Ом]

Z9, [Ом]

Z10, [Ом]

Z11, [Ом]

Z13, [Ом]

ik

Ваттметр

Значение

j30

j41

j50

j25

-j55

75

-j35

9

i10

1, 3

Пояснения к таблице 1:

В таблице использованы следующие обозначения:

i₁₀ – рассчитывается мгновенное значение тока через сопротивление Z10;

Ваттметр: 1, 3 – ваттметр включается в одну из ветвей между узлами 1 и 3;

Вектора: должна быть построена векторная диаграмма для тока, протекающего по цепи с ваттметром, и напряжения между узлами этой ветви.

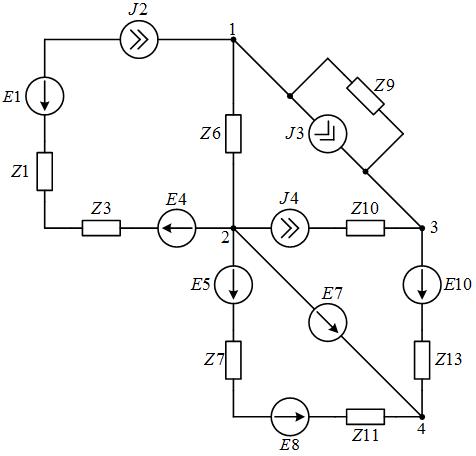
Рис. 1. Исходная схема

Содержание задания

Для электрической цепи переменного синусоидального тока, соответствующей индивидуальному заданию, необходимо выполнить следующие расчеты и графические построения:

1. Составить систему уравнений по законам Кирхгофа в интегрально-дифференциальном виде для мгновенных значений напряжений и токов.

2. Выполнить расчет токов в ветвях электрической цепи методом узловых потенциалов, с проверкой правильности расчетов посредством баланса мощностей и оценкой их точности.

3. Определить режимы работы источников, имеющихся в заданной электрической цепи.

4. Рассчитать ток в указанной ветви методом эквивалентного генератора (МЭГ).

5. Для заданного тока i(t) построить график мгновенных значений.

6. Рассчитать показание ваттметра, включенного в одну из ветвей электрической цепи.

7. Построить векторную диаграмму токов и напряжений для ветви, в которой включен ваттметр.

Система уравнений по законам Кирхгофа

Система уравнений по законам Кирхгофа в интегрально-дифференциальном виде для мгновенных значений токов и напряжений

Произвольно выбираем условно-положительные направления токов в ветвях и направления обхода контуров – по часовой стрелке (рис. 2).

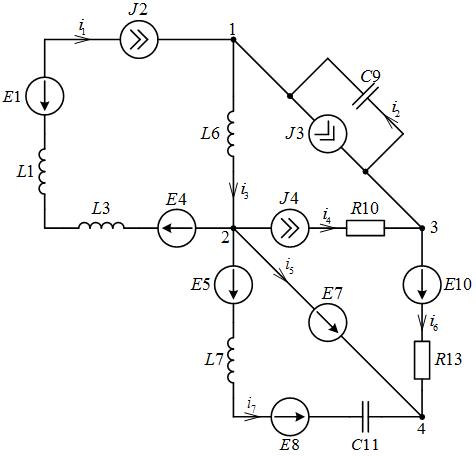
Рис. 2. Схема цепи к составлению уравнений по законам Кирхгофа

В рассматриваемой схеме: узлов , ветвей , независимых контуров . Следовательно, по первому закону Кирхгофа должно быть составлено уравнения, а по второму закону Кирхгофа уравнений.

Для мгновенных значений токов, напряжений и ЭДС система уравнений по законам Кирхгофа имеет вид:

С учетом того, что:

система уравнений записывается в виде:

Метод узловых потенциалов и баланс мощностей

Запишем комплексы действующих значений ЭДС и токов источников:

Расчетная схема с комплексными источниками ЭДС и тока и комплексными сопротивлениями ветвей показана на рис. 3.

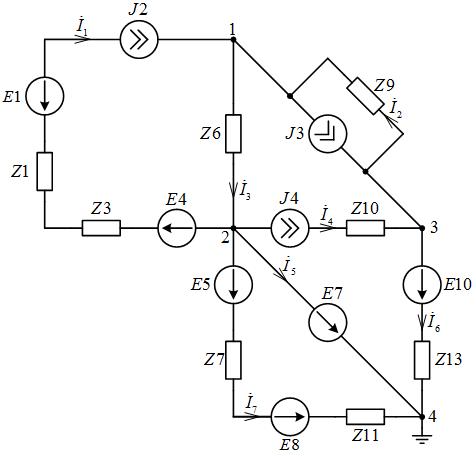
Рис. 3. Схема цепи к методу узловых потенциалов

Принимаем потенциал узла 4 равным нулю, тогда потенциал узла 2:

В.

Составляем систему уравнений:

Подставляем в систему исходные данные:

Решая систему уравнений, получаем значения узловых потенциалов:

Определяем значения токов в ветвях:

Составим баланс мощности.

Полную мощность источников определим по формуле:

Найдем напряжения на источниках тока по 2-му закону Кирхгофа:

Полная мощность источников:

Активная мощность источников равна , реактивная - .

Активная мощность потребителей:

Реактивная мощность потребителей:

Погрешность расчета мощностей:

- по активной мощности:

- по реактивной мощности:

Режимы работы источников

Режимы работы источников электроэнергии определяются следующим образом: рассчитывается активная мощность источника, и, если она имеет знак «плюс», то источник работает в режиме генерирования электроэнергии, если знак «минус» - в режиме потребления.

Определяем режимы работы источников электроэнергии:

- источник Е1 работает в режиме потребителя;

- источник Е4 работает в режиме потребителя;

- источник Е5 работает в режиме потребителя;

- источник Е7 работает в режиме потребителя;

- источник Е8 работает в режиме потребителя;

- источник E10 работает в режиме потребителя;

- источник J2 работает в режиме потребителя;

- источник J3 работает в режиме генератора;

- источник J4 работает в режиме генератора.

Действующее значение тока через заданное сопротивление методом эквивалентного генератора

Исключим из схемы ветвь 2-3, содержащую сопротивление Z10, и определим мгновенное значение тока через эту ветвь (рис. 4).

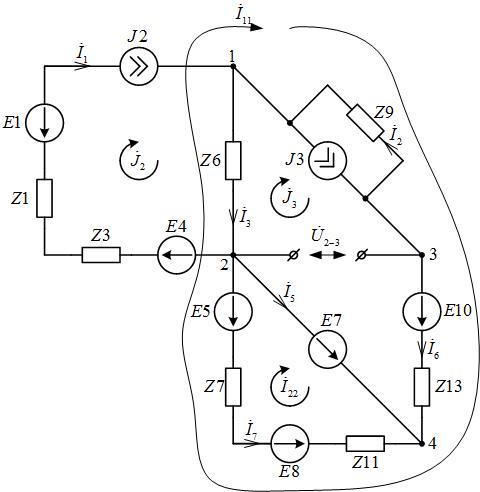
Рис. 4. Схема эквивалентного генератора напряжения

Для того, чтобы по второму закону Кирхгофа и по закону Ома определить напряжение , нужно рассчитать значение тока :

.

Рассчитаем ток при помощи метода контурных токов. Составляем систему уравнений:

Подставим в систему известные значения ЭДС, сопротивлений и тока источника и упростим ее:

Решая систему уравнений, получаем значения контурных токов:

По первому закону Кирхгофа определяем ток :

Определяем напряжение холостого хода:

Исключим из схемы все источники электроэнергии и определим внутреннее сопротивление двухполюсника (рис. 5).

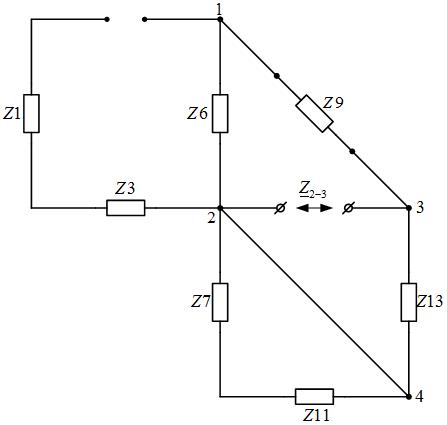
Рис. 5

Определяем внутреннее сопротивление активного двухполюсника:

Ом.

Определяем значение тока :

График мгновенных значений заданного тока

Запишем мгновенное значение тока :

График мгновенных значений тока показан на рис. 6.

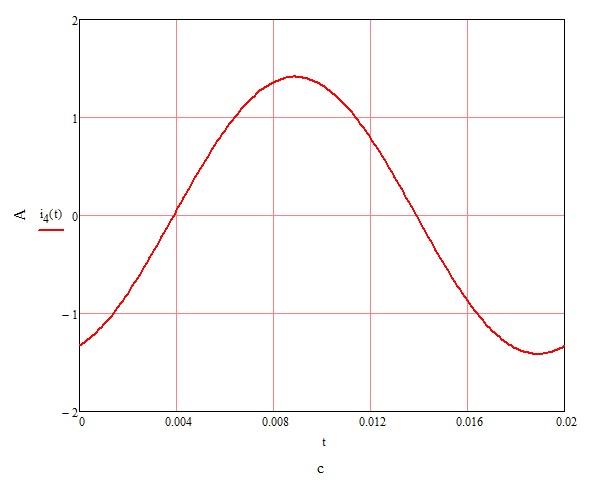
Рис. 6. График мгновенных значений тока i₄

Расчет показания ваттметра

Изобразим схему включения ваттметра для измерения активной мощности в ветви 1-3 (рис. 7).

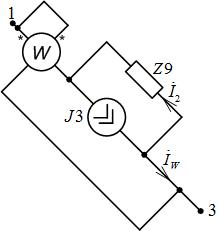
Рис. 7. Ветвь с ваттметром

Напряжение на обмотке ваттметра:

Ток, протекающий через токовую обмотку ваттметра, равен:

Показание ваттметра:

 Векторная диаграмма тока и напряжения заданной ветви

Напряжение между точками 1 и 3 было найдено в предыдущем пункте:

Ток ветви .

Векторная диаграмма показана на рис. 8.

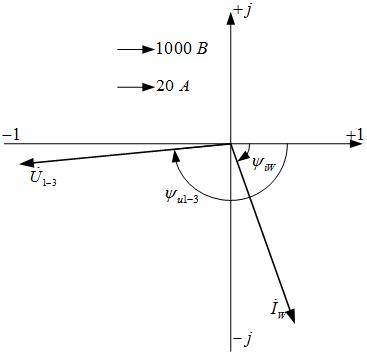
Рис. 8. Векторная диаграмма тока и напряжения ветви с ваттметром

Заключение

В ходе выполнения курсовой работы были выполнены следующие задачи:

1. Составлены уравнения для заданной цепи по первому и второму законам Кирхгофа в интегрально-дифференциальной форме.

2. Выполнен расчет токов цепи методом контурных токов и составлен баланс мощностей источников и потребителей.

3. Определены режимы работы источников ЭДС и тока.

4. Определен ток заданной ветви методом эквивалентного генератора, а также построен график его мгновенных значений.

5. Рассчитано показание ваттметра, включенного в заданную ветвь, и построена векторная диаграмма тока и напряжения этой ветви.

Список использованной литературы

1. Общая электротехника. Под ред. Пантюшина. Учебник для машиностроит., горных, металлургич. теплоэнергетич. специальностей вузов. М., «Высш. школа», 1970.

2. Электротехника/Ю. М. Борисов, Д. Н. Липатов, Ю.Н. Зорин. Учебник для вузов. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1985. – 552 с., ил.

3. Иванов И. И., Соловьев Г. И. Электротехника: Учебное пособие. 6-е изд., стер. – СПб.: Издательство «Лань», 2009. – 496 с.: ил. – (Учебники для вузов. Специальная литература).