Математическая обработка динамических рядов - определение и вычисление с примерами решения
Содержание:
Понятие о динамических рядах:
Динамическим рядом называют ряд показателей, характеризующих величину какого-либо явления по состоянию в определенные моменты или периоды (интервалы) времени. Существует три разновидности динамических рядов:
а) Моментные ряды, образованные показателями, измеряющими явление на определенные моменты времени.
Пример 1. Списочная численность рабочих предприятия.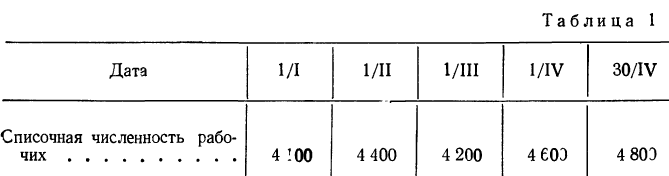
б) Интервальные ряды, образованные показателями, измеряющими явления за какой-нибудь промежуток времени или интервал.
Пример 2. Фонд заработной платы рабочих предприятия.

в) Ряды производные (средних или относительных величин), образованные показателями, характеризующими моменты или интервалы времени с помощью средних или относительных величин.
Пример 3. Среднемесячная заработная плата рабочих предприятия.

Приемы обработки динамических рядов
Очень часто уровни динамических рядов колеблются; при этом тенденция (основное направление) развития явления во времени скрыта случайными отклонениями уровней в ту или иную сторону. Поэтому возникает необходимость преобразования рядов для выявления закономерностей его развития.
Разберем некоторые приемы преобразования рядов.
1. Использование среднего абсолютного прироста. Приростами динамического ряда называются разности между последующими уровнями ряда и предыдущими (обозначаются 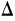 ). Так, если имеется динамический ряд:
). Так, если имеется динамический ряд:  то приросты получатся соответствующим вычитанием:
то приросты получатся соответствующим вычитанием:

Число приростов на единицу меньше числа уровней ряда, т. е. составляет n—1. Найдем средний прирост ряда:
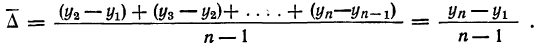
Таким образом: 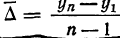
Найденный средний абсолютный прирост позволяет путем последовательного прибавления его к первому фактическому уровню найти последующие уровни, отличающиеся от фактических тем, что они вычислены в предположении их плавного возрастания (или убывания), без скачков.
Рассмотрим такое преобразование динамического ряда на. примере.
Пример 4. Преобразуем ряд динамики месячного фонда заработной платы рабочих, приведенный в табл. 2, способом среднего прироста.
1) Находим средний прирост по формуле 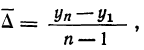
где 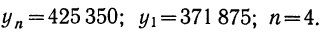
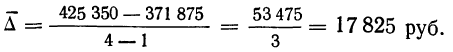
2) Находим плавные уровни:
- а) второй
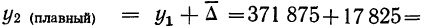
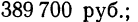
- б) третий
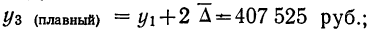
- в) четвертый
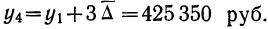
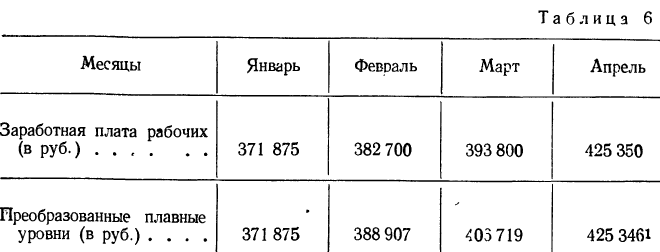
Располагаем фактические и исчисленные данные в одну таблицу.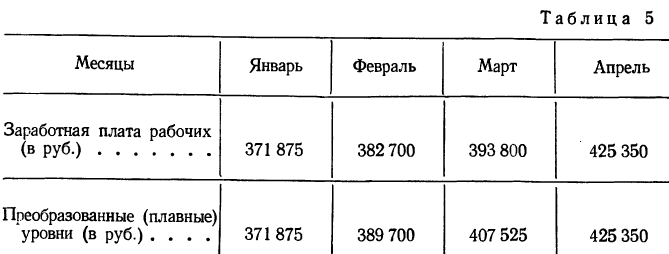
При таком преобразовании первый и последний уровни остаются без изменения.
2. Использование среднего коэффициента или темпа роста. Коэффициентом роста называют отношение последующего уровня ряда динамики к предыдущему уровню того же ряда. Если выразить коэффициент роста в процентах, то получим темп роста.
Имеется динамический ряд:
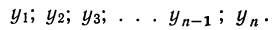
Коэффициенты роста (обозначаются 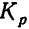 ) будут представлять собой отношения:
) будут представлять собой отношения:
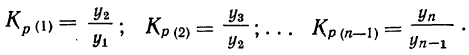
Следует обратить внимание на то обстоятельство, что число коэффициентов роста (так же, как и приростов) меньше числа уровней на единицу.
Вычисление среднего коэффициента роста производят по формуле средней геометрической.
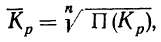
где n — число коэффициентов роста.
Учитывая, что произведение всех коэффициентов роста равно
отношению последнего уровня (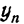 ) к первому (
) к первому (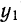 ) и заменяя
) и заменяя 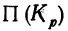 равным ему отношением
равным ему отношением 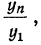 получаем:
получаем:
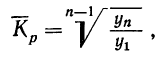
где n — число уровней.
Найденный средний коэффициент роста используется аналогично использованию среднего абсолютного прироста (см. предыдущий пример) с той разницей, что первый фактический уровень умножается на средний коэффициент роста в соответствующей степени.
Пример 5. Используя данные табл. 2, преобразовать ряд динамики месячного фонда заработной платы рабочих способом среднего коэффициента роста.
Решение: 1) Находим средний коэффициент роста: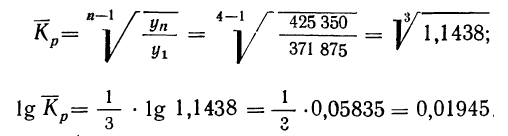
откуда 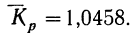
2) Находим плавные уровни:
а) второй плавный уровень: 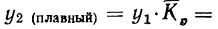
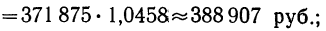
б) третий плавный уровень: 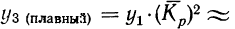
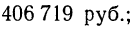
в) четвертый уровень: 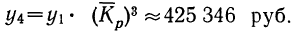 Располагаем фактические и преобразованные данные в одну таблицу.
Располагаем фактические и преобразованные данные в одну таблицу.
Механическое сглаживание
Кроме рассмотренных приемов преобразования динамических рядов, для нахождения плавных уровней путем использования среднего прироста или среднего коэффициента роста применяется метод механического сглаживания ряда скользящей средней.
Существует две разновидности сглаживания: методом невзвешенной и взвешенной скользящей средней.
Невзвешенная скользящая средняя. Применение метода сглаживания невзвешенной скользящей средней состоит в замене абсолютных данных средними арифметическими за определенные периоды. При выборе этих периодов мы производим скольжение, постепенно исключая из периода первые уровни и включая последующие.
Различают два случая: 1) когда период сглаживания состоит из нечетного числа членов; 2) когда период сглаживания состоит из четного числа членов.
Разберем 1-й случай.
Пример 6.
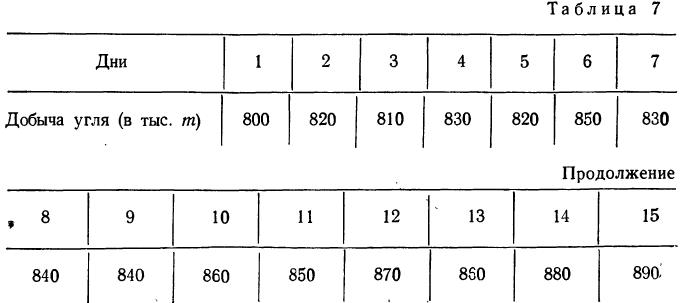
Требуется сгладить ряд методом незвешенной скользящей средней с трехдневным периодом (взято нечетное число дней).
Решение. Для сглаживания ряда методом скользящей средней (с трехчленным периодом) строим следующую таблицу:
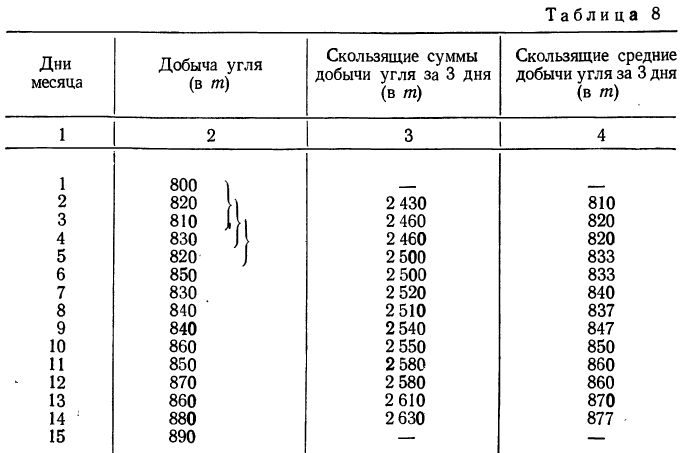
При использовании этого способа найденные скользящие средние (колонка 4) располагаются в середине (центре) периода (первая скользящая средняя относится ко второму дню, вторая— к третьему дню и т. д.), т. е. являются центрированными.
После вычисления скользящих средних их вместе с фактическими данными наносят на график (см. график 1).
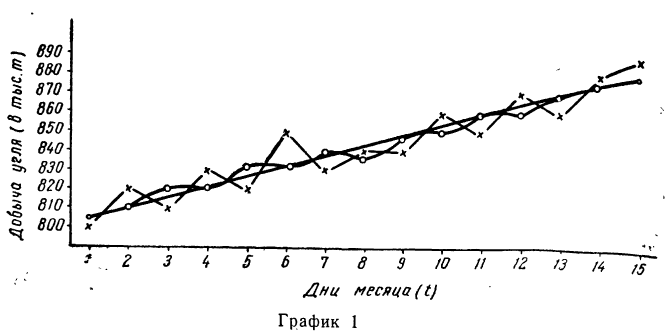
Разберем второй случай (с четным числом членов периода).
Пример 7. По данным примера 6 сгладить ряд методом невзвешенной скользящей средней с четырехдневным периодом (взято четное число дней).
Решение. Для сглаживания ряда методом скользящей средней (с четырехчленным периодом) строим следующую таблицу:
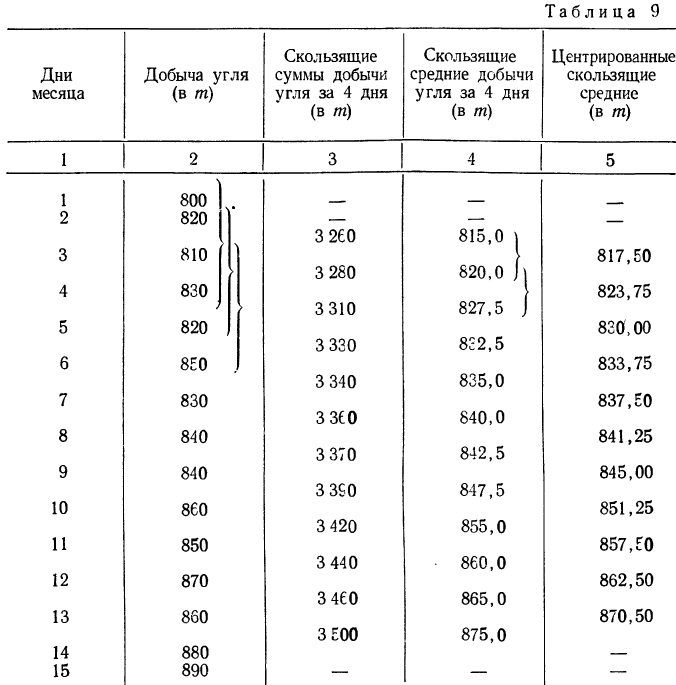
При использовании этого способа следовало найденные скользящие средние с четырехчленным периодом (колонка 4), как и в первом случае — с трехчленным периодом, — отнести к центру периода. Но этот центр не совпадает с определенной датой. Поэтому прибегают к приему, называемому центрированием и состоящему в нахождении средних (центра) между каждой парой уже найденных скользящих средних. Полученные средние называются центрированными средними (колонка 5).
После вычисления центрированных скользящих средних их вместе с фактическими данными наносят на график.
Взвешенная скользящая средняя. Вторая разновидность этого метода сглаживания состоит в применении взвешенной скользящей средней. Для определения весов можно представить себе многократно повторенное сглаживание скользящей средней с двучленным периодом.
Первые скользящие средние:
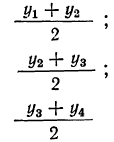
и т.д.
Используя найденные скользящие средние, получаем вторые скользящие средние (для трехчленного периода):
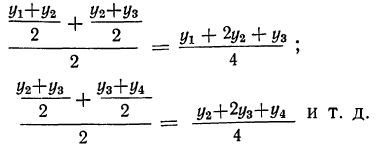
Еще одно применение скольжения (для четырехчленного периода) дает:
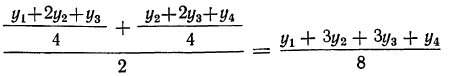
и далее для пятичленной средней:
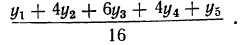
Веса уровней ряда при сглаживании образуют коэффициенты бинома:
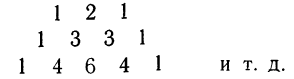
Ограничиваясь пятичленной взвешенной скользящей средней, рассмотрим ее практическое использование. Этот метод можно применять путем использования трафарета, имеющего следующий вид:
Этот трафарет прикладывается (слева) к фактическим данным, подлежащим сглаживанию.
Умножая фактические данные на веса (коэффициент трафарета), находим сумму произведений. Первую сумму записываем против коэффициента 6, затем передвигаем трафарет на одну строку вниз и умножением фактических данных на коэффициенты трафарета находим вторую сумму и т. д. Все найденные суммы делятся на 16 (сумму всех весов).
Пример:
По данным примера 6 сгладить ряд методом взвешенной скользящей средней с пятичленным периодом.
Решение. Располагаем все данные в таблицу и производим соответствующие расчеты передвижением трафарета на одну строку вниз.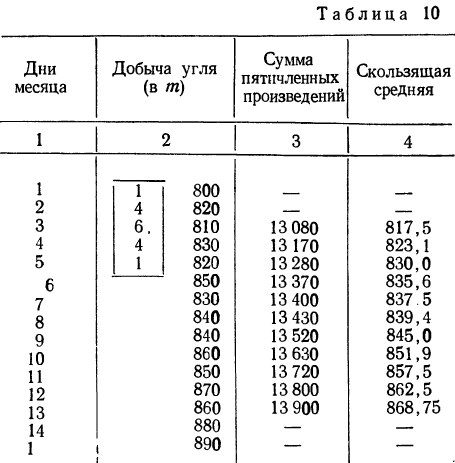
Аналитическое выравнивание
Очень часто для преобразования динамического ряда применяют аналитическое выравнивание. Имеются следующие фактические уровни ряда:
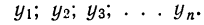
Характер изменения этих уровней, т. е. движения динамического ряда, может быть различным. Нашей задачей является нахождение такой простой математической формулы, которая давала бы возможность вычислить теоретические уровни. Основное требование, предъявляемое к этой формуле, состоит в том, что уровни, исчисленные по ней, должны воспроизводить общую тенденцию фактических уровней. Нахождение этой формулы называется аналитическим выравниванием, представляющим собой не что иное, как удобный способ описания эмпирических данных. При этом обычно употребляют ограниченное число типов таких формул: прямой линии, параболы второго или третьего порядка, гиперболы и показательной функции. Общие соображения при выборе типа линии, по которой производится аналитическое выравнивание, могут быть сведены к следующим:
1) Если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины, то математической функцией, уравнение которой можно принять за основу аналитического выравнивания, следует считать прямую линию: 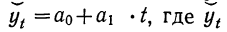 читается как у, выравненный по t.
читается как у, выравненный по t.
Если приросты приростов уровней, т. е. ускорения, колеблются около постоянной величины, то за основу аналитического выравнивания следует принять параболу второго порядка:
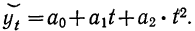
Показатели 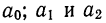 представляют собой в каждом отдельном случае выравнивания постоянные величины, называемые параметрами:
представляют собой в каждом отдельном случае выравнивания постоянные величины, называемые параметрами: 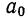 — начальный уровень (при условии, что первое значение t есть нуль);
— начальный уровень (при условии, что первое значение t есть нуль); 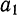 — начальная скорость ряда и
— начальная скорость ряда и 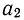 ускорение или вторая скорость.
ускорение или вторая скорость.
3) Если уровни изменяются с приблизительно постоянным относительным приростом, то выравнивание производится по показательной (экспонентной) функции:
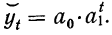
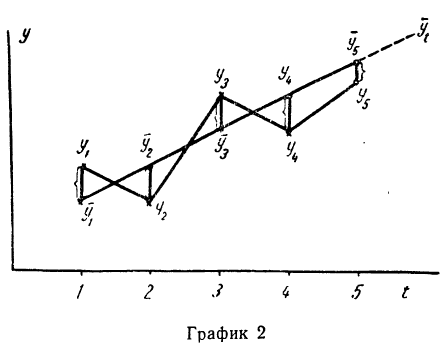
Для нахождения аналитического уравнения, по которому производится выравнивание уровней динамического ряда, применяют различные способы. Один из способов состоит в расчленении динамического ряда на две примерно^ равные части; при этом сумма выравненных значений в каждой части должна совпадать с суммой фактических значений, или, иными словами, сумма отклонений фактических данных от выравненных равняется нулю, т. е.
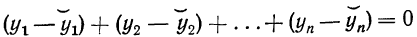 (см. график 2).
(см. график 2).
Это требование может быть записано в таком виде:
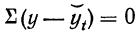 или в случае прямой линии
или в случае прямой линии 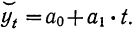
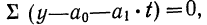
откуда
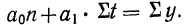
Если применить это требование к каждой из двух частей ряда, то, вычисляя для каждой части динамического ряда все необходимые данные, т. е. 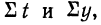 получим два уравнения с двумя неизвестными. В результате решения этой системы уравнений находятся параметры
получим два уравнения с двумя неизвестными. В результате решения этой системы уравнений находятся параметры 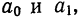 т. е. начальный уровень и скорость ряда.
т. е. начальный уровень и скорость ряда.
Недостатком указанного метода является то, что при произвольном расчленении ряда на две части (группы) мы получаем различные результаты. Несмотря на это, данный способ может найти широкое применение.
Пример 9.
Рассмотрим применение описанного способа на конкретных данных. Возьмем из примера 6 данные о добыче угля и произведем выравнивание уровней по прямой:
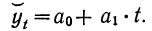
Решение. Так как имеются данные за 15 дней, то расчленение периода на примерно равные части дает в первой 7, во второй 8 дней.
Имеем: для первой части 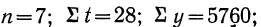
для второй части 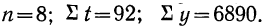
Составляем систему уравнений:
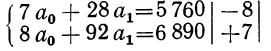
Уравниваем коэффициенты при ао путем умножения первого уравнения на —8, а второго на + 7.
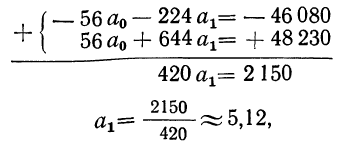
откуда
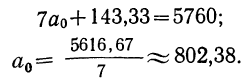
Следовательно, аналитическое уравнение прямой примет следующий вид:
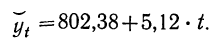
Подставляя значения t в найденное уравнение, получаем: 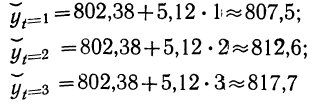
и т. д. (см. табл. 11).
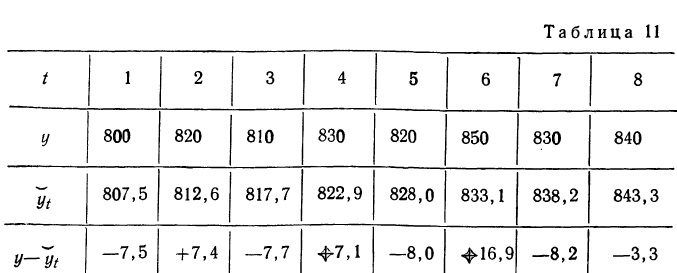
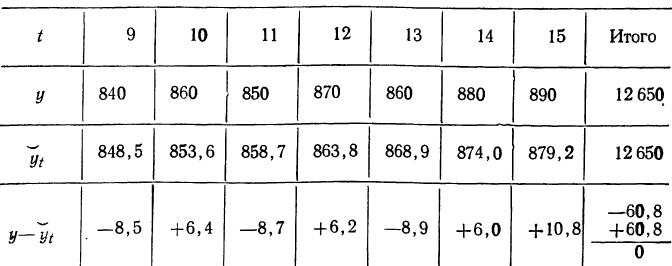
Как видно из разобранного примера, выравненные данные довольно хорошо воспроизводят фактические. Сумма их отклонений от фактических уровней равна нулю. При выравнивании по параболе второго порядка 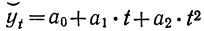 (где нужно знать три параметра) весь ряд следует расчленить на три части и решать систему трех уравнений с тремя неизвестными.
(где нужно знать три параметра) весь ряд следует расчленить на три части и решать систему трех уравнений с тремя неизвестными.
Второй способ — наименьших квадратов — основан на требовании о том, чтобы сумма квадратов отклонений фактических данных от выравненных (см. график 2) была наименьшей:
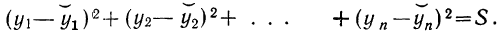
,S должно быть наименьшим (минимальным).
Принцип, положенный в основу метода наименьших квадратов, может быть записан в сжатом математическом виде следующим образом:
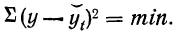
Из курса высшей математики известно, что при нахождении минимума функции нужно найти частные производные и приравнять их нулю. Найдем минимум данной функции, используя уравнение прямой линии.
имеем:
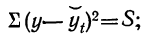
заменяем:
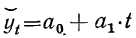
и получаем:
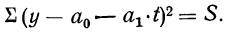
Находим частные производные функции S сначала по параметру 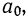 а затем по
а затем по 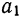 и приравниваем их нулю.
и приравниваем их нулю.
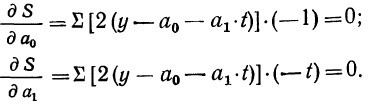
Преобразовывая, получаем:
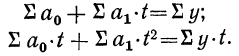
На основании свойства сумм (см. стр. 11) выносим 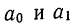 за знак суммы.
за знак суммы.
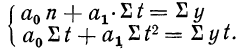
Полученная система называется системой нормальных уравнений для нахождения параметров 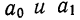 при выравнивании по прямой линии.
при выравнивании по прямой линии.
Аналогично получаем систему нормальных уравнений при выравнивании по параболе второго порядка:
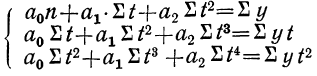
Выравнивание по прямой линии
Покажем выравнивание по прямой линии на следующем примере.
Пример 10.
Поданным примера б произвести выравнивание по прямой линии методом наименьших квадратов.
Решение. Аналитическое уравнение прямой линии имеет вид:
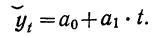
Для нахождения параметров 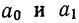 следует решить систему нормальных уравнений:
следует решить систему нормальных уравнений:
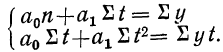
Для вычисления всех необходимых исходных данных построим расчетную таблицу (см. табл. 12).
Составляем систему нормальных уравнений:
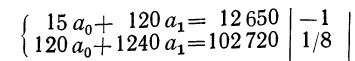
Уравниваем коэффициенты при 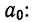
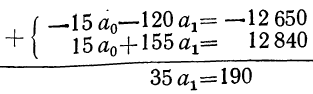
Значит, 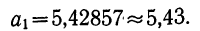
Из первого уравнения находим 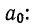
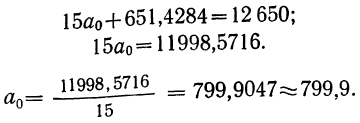
После определения 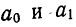 составляем аналитическое уравнение:
составляем аналитическое уравнение:
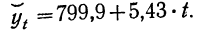
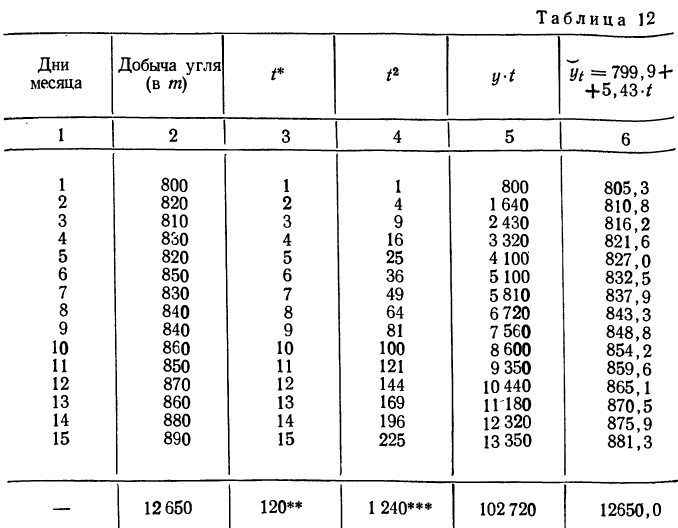
Подставляя значения t, получаем:
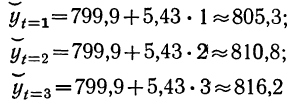
и т. д. (см. колонку 6, табл. 12).
При заполнении колонки 3 со значениями t производим нумерацию дат. Так, если бы в примере были годы или дни (понедельник, вторник и т. д.), мы, прибегая к нумерации, вели бы счет с первой даты, принимая t равным единице, двум и т. д.
Итог колонки 3 может быть найден без суммирования по формуле:
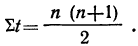
Проверим наш пример:
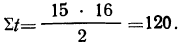
Итог колонки 4 можно определить по формуле и без предварительно, го возведения в квадрат всех значений t:
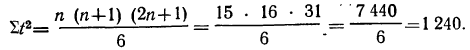
После вычислений всех значений 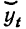 наносим фактические данные и выравненные по прямой линии на один график (см. график 1, стр. 212).
наносим фактические данные и выравненные по прямой линии на один график (см. график 1, стр. 212).
Упрощенный метод выравнивания по прямой линии
Выравнивание по прямой линии методом наименьших квадратов можно значительно упростить соответствующим подбором способа отсчета t так, чтобы 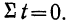 При этом различают два случая:
При этом различают два случая:
- Когда число членов динамического ряда нечетное, то следует отсчитывать t от середины ряда. При таком отсчете значение серединной даты (или периода) динамического ряда принимается равным 0, ранние даты имеют отрицательные значения (—1; —2; —3 и т. д.), а поздние даты — положительные значения (1; 2; 3 и т. д.).
- Когда число членов ряда четное, то в этом случае для соблюдения требований о равных интервалах между всеми значениями t и о том, чтобы сумма всех значений t равнялась нулю, подбор t производится так: находится серединная пара дат (или периодов), и значения t для нее принимают —1 и +1, а далее вверх идут —3; —5; —7 и т. д., и вниз +3; +7; +9 и т. д.
При таком способе отсчета t система нормальных уравнений упрощается и принимает вид:
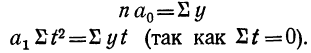
Тогда:
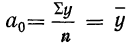 (средняя арифметическая);
(средняя арифметическая);
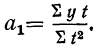
Пример 11.
Для практического использования данного метода рассмотрим предыдущий пример.
Выравнивание по прямой линии (упрощенным методом) (см. табл. 13).
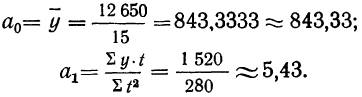
Тогда аналитическое уравнение примет вид:
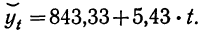
При различных значениях t получаем:
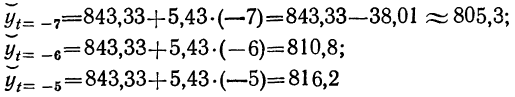
и т. д. (см. колонку б табл. 13).
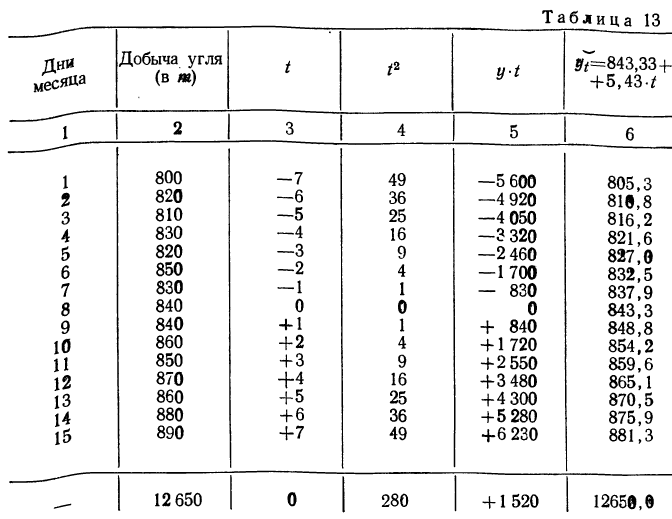
Фактические данные и выравненная прямая изображены на графике 3.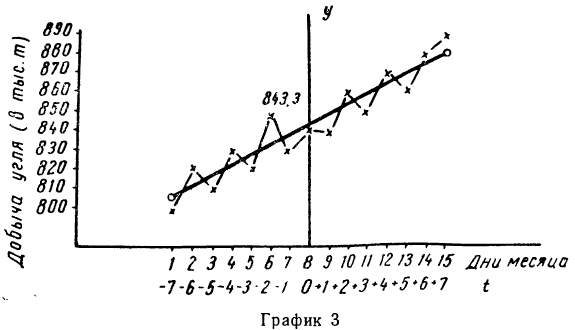
Следует заметить, что в случае выравнивания по прямой линии упрощенным методом параметр 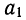 продолжает играть ту же роль, что и при обычном выравнивании, т. е. представляет собой скорость ряда; значение параметра
продолжает играть ту же роль, что и при обычном выравнивании, т. е. представляет собой скорость ряда; значение параметра 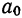 изменяется. Если при обычном выравнивании
изменяется. Если при обычном выравнивании 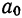 —это начальный уровень, то при упрощенном методе выравнивания
—это начальный уровень, то при упрощенном методе выравнивания 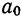 —это средний уровень явления (см. график 3).
—это средний уровень явления (см. график 3).
Выравнивание по параболе второго порядка
Аналитическое уравнение параболы имеет вид:
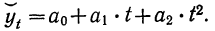
Что касается системы нормальных уравнений, то подбором способа отсчета t упростим нахождение параметров, так как
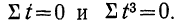
Получим:
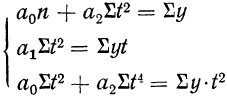
Пример 12.
В табл. 14 приведены данные о производстве изделия А по годам.
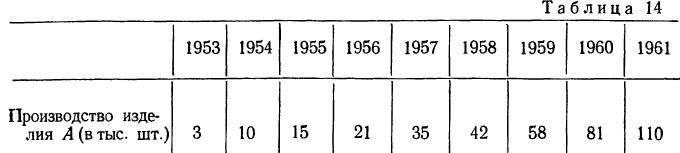
Выровнять эти данные по параболе второго порядка и изобразить графически.
Решение. Для получения сумм, входящих в систему нормальных уравнений, построим расчетную таблицу.
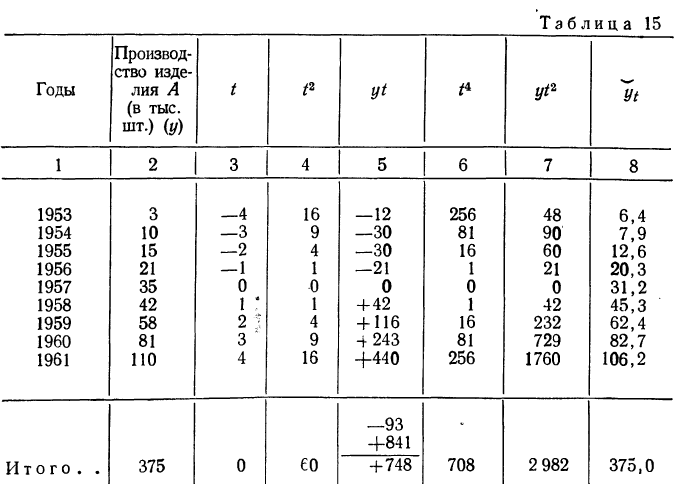
Составляем систему нормальных уравнений:
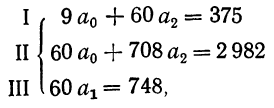
откуда
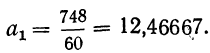
Делим первое уравнение на 9, а второе на 60:
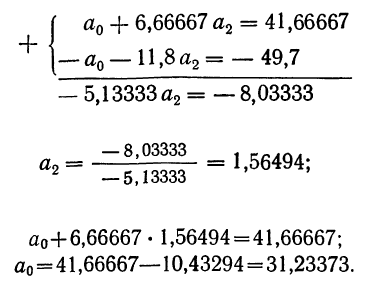
Таким образом,
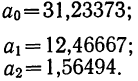
Производим проверку найденных параметров:
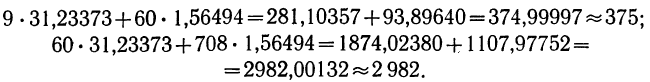
Аналитическое уравнение параболы примет следующий вид: 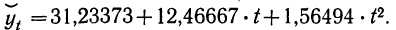
После решения системы нормальных уравнений всегда следует проверить найденные параметры. Однако в дальнейшем производить проверку на страницах пособия мы не будем, предоставляя возможность читателю сделать это самостоятельно, путем подстановки в нормальные уравнения.
Подставляя значения t (от —4 до +4), получим выравнен ные значения производства изделия А (см. колонку 8 табл.15)

Теперь можно построить график, изобразив фактические данные и выравненные по параболе второго порядка аналогично тому, как это было показано при сглаживании методом скользящей средней и выравнивании по прямой линии.
Выравнивание по показательной (экспонентной) функции производится в том случае, если уровни изменяются с более или менее постоянным относительным приростом (по правилу сложных процентов). Выравнивание производится по следующей формуле: 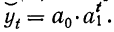 В этом случае параметры
В этом случае параметры 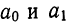 определяются по методу наименьших квадратов отклонений логарифмов путем решения системы нормальных уравнений:
определяются по методу наименьших квадратов отклонений логарифмов путем решения системы нормальных уравнений:
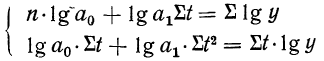
При способе отсчета t таким образом, чтобы 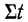 =0, мы получаем:
=0, мы получаем:
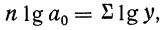
откуда
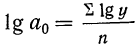
и
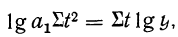
откуда
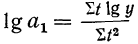
Пример 13.
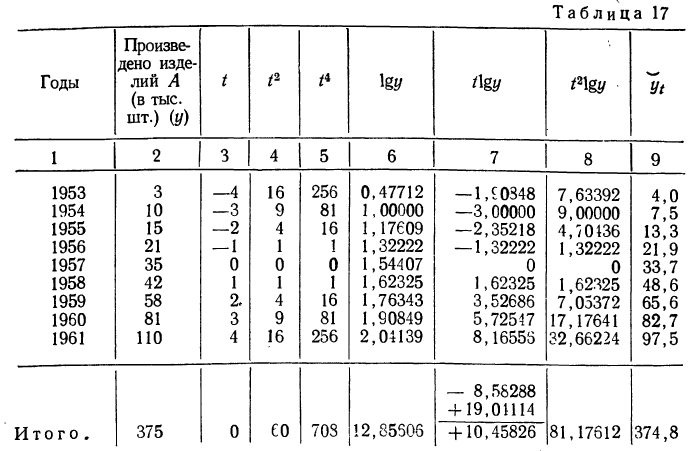
Для иллюстрации произведем выравнивание по показательной функции динамического ряда, рассмотренного в примере 12 (см. табл. 14). Для получения исходных данных построим расчетную табл. 16.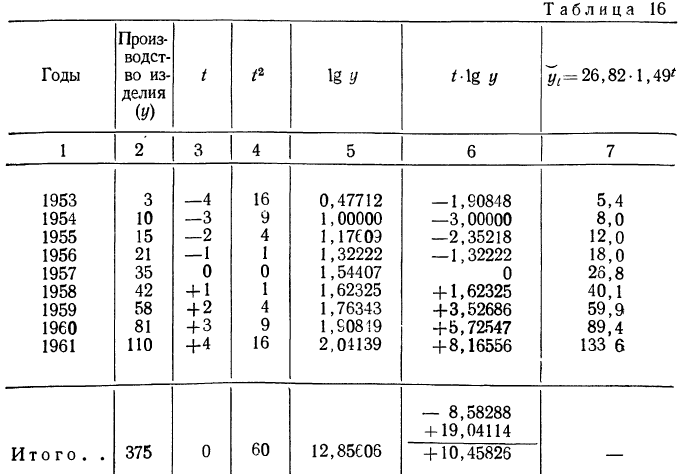
Получаем:
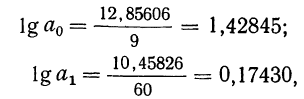
откуда 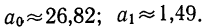
Аналитическое уравнение показательной кривой примет вид: 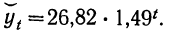
Подставляем значения t и получаем (см. колонку 7 табл. 16):
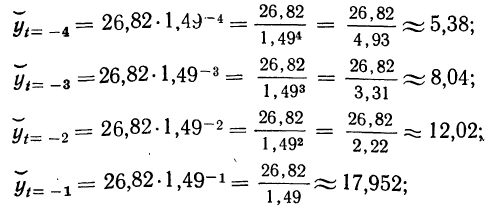
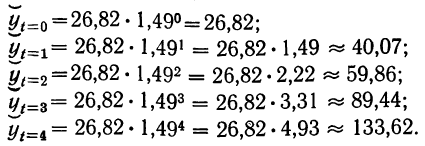
Полученные выравненные уровни, а также фактические данные можно нанести на график.
В некоторых случаях более сложного изменения уровней динамического ряда можно применять выравнивание по параболе второго порядка с логарифмированием уровней по формуле:
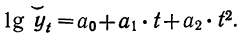
Это будет означать выравнивание уровней по показательной функции следующего вида:
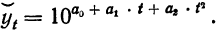
В этом случае параметры 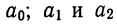 определяются методом наименьших квадратов из системы нормальных уравнений.
определяются методом наименьших квадратов из системы нормальных уравнений.
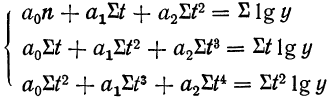
При условии 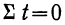 получаем:
получаем:
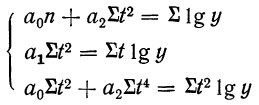
Пример 14.
Проиллюстрируем ход действий при выравнивании динамического ряда по. показательной функции 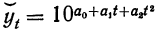 (упрощенным способом), используя данные предыдущего примера.
(упрощенным способом), используя данные предыдущего примера.
Получаем:
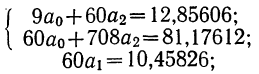
откуда
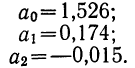
Следовательно, 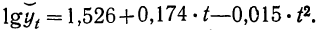
Подставляя значения t, равные —4, —3, —2 и т. д., получаем значения 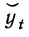 (см. колонку 9 табл. 17).
(см. колонку 9 табл. 17).
Интерполяция уровней
Интерполяцией называется нахождение промежуточных неизвестных уровней динамического ряда при наличии известных соседних уровней.
Интерполяция может производиться различными способами:
1) путем использования только двух уровней и 2) путем использования нескольких уровней.
Различные предположения о динамике развития явления при интерполяции приводят, естественно, к различным результатам. Поэтому практически при выборе того или иного предположения о тенденции развития изучаемого явления обычно просматривают динамический ряд до или после (можно и одновременно) интерполируемого периода и приходят к тому или иному заключению.
Рассмотрим применение интерполяции на конкретных примерах.
1. Имеются данные о выпуске продукции за 1956 и 1958 гг. Требуется произвести интерполяцию и вычислить предполагаемый уровень 1957 г.
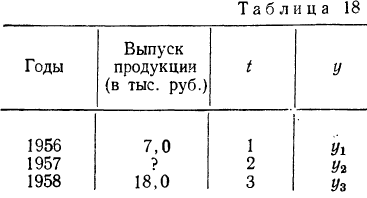
а) Предполагая, что выпуск продукции увеличивался с постоянным приростом, равным
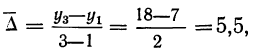
и, прибавляя его к начальному уровню, получим уровень 1957 г.
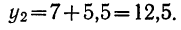
Это равносильно определению уровня 1957 г. как полусуммы продукции 1956 и 1958 гг.
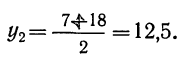
б) Предположим, что уровни .выпуска продукции за эти годы менялись с постоянным (средним) коэффициентом роста. Найдем его:
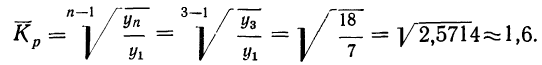
Тогда 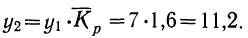
2. а) Пусть наряду с двумя известными уровнями выпуска продукции за 1956 и 1958 гг. известен еще один уровень, за 1955 г., равный 3 тыс. руб. Тогда, предполагая, что изменение выпуска продукции происходило по параболе второго порядка, получим:

Составляем систему трех уравнений с тремя неизвестными:
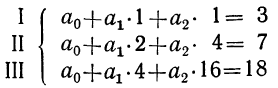
Вычитая из второго уравнения первое, получим новое уравнение уже не с тремя, а с двумя неизвестными:
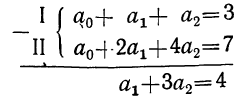
Вычитаем из третьего уравнения второе:
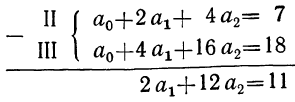
Получилась система двух уравнений с двумя неизвестными: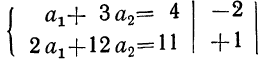
Решим ее:
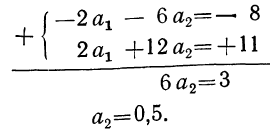
Тогда
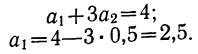
Подставляя значения 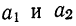 в первое уравнение, получаем:
в первое уравнение, получаем:
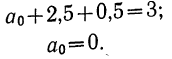
Следовательно, 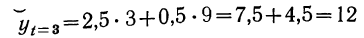 тыс. руб.
тыс. руб.
Этот же результат можно получить, пользуясь методом конечных разностей. Зная уровни, найдем первые и вторые разности.
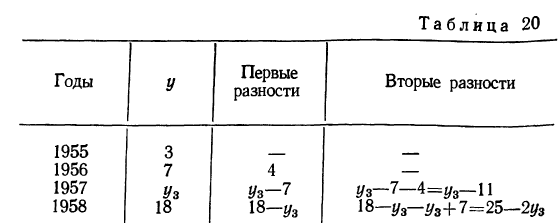
Если исходить из предположения об изменении выпуска продукции по параболе второго порядка, то вторые разности (т. е. ускорения) должны быть постоянными.
Тогда
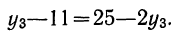
Отсюда
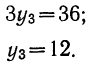
б) Интерполяция путем использования нескольких уровней, предшествующих неизвестным и последующих за ними, может быть произведена при помощи выравнивания способом наименьших квадратов.
Например, имеются уровни за 1954, 1955, 1956, 1959, 1960 и 1961 гг. Методом интерполяции рассчитать уровни 1957 и 1958 гг.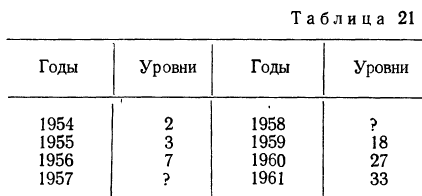
Предполагая, что уровни 1957 и 1958 гг. укладываются в общую тенденцию изменения уровней, произведем выравнивание по прямой линии способом наименьших квадратов, используя следующую таблицу:
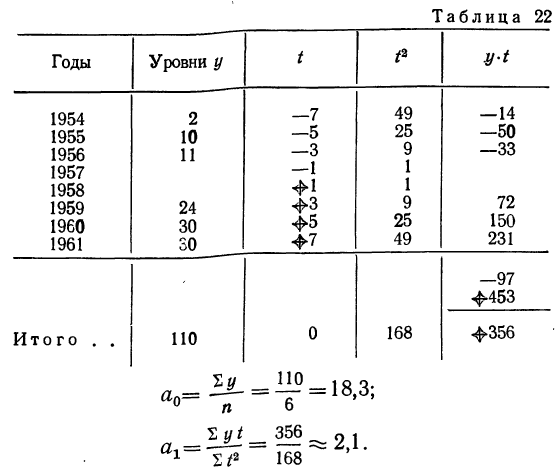
Значит, 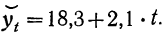
Следовательно, для 1957 г. при ( t=— 1)
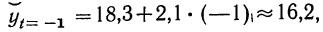
а для 1958 г. (при t= + l).
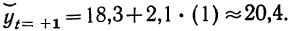
Данным методом пользуются в тех случаях, когда уровни определенных периодов известны, но искажены действием каких-либо факторов, влияние которых необходимо оценить. Достигается это нахождением разностей между фактическими и выравненными уровнями.
Пусть нам известны уровни 1957 г.— 13. и 1958 г. — 16 единиц, искаженные действием определенного фактора (изменение, например, технологического процесса в эти годы или др.). Тогда можно оценить суммарное воздействие данного фактора на величину уровней (см. табл. 23).
Интерполяция в демографической статистике
Имеется ряд способов интерполяции, разработанных применительно к статистике населения. Они применяются при использовании надежных данных о численности населения по пятилетним интервалам для сглаживания возрастного распределения (т. е. интерполяции) и нахождения численности населения по каждому годичному интервалу внутри пятилетних интервалов, для сглаживания таблиц смертности и т. п.
Идея этих способов состоит в использовании скользящих, парабол различных порядков. Из числа этих способов рассмотрим два.

1) Способ С. А. Новосельского основан на применении для каждого пятилетнего интервала своей параболы второго порядка: 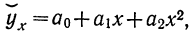 где х — возраст;
где х — возраст; 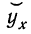 —выравненное значение численности населения в каждом возрасте;
—выравненное значение численности населения в каждом возрасте; 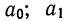 и
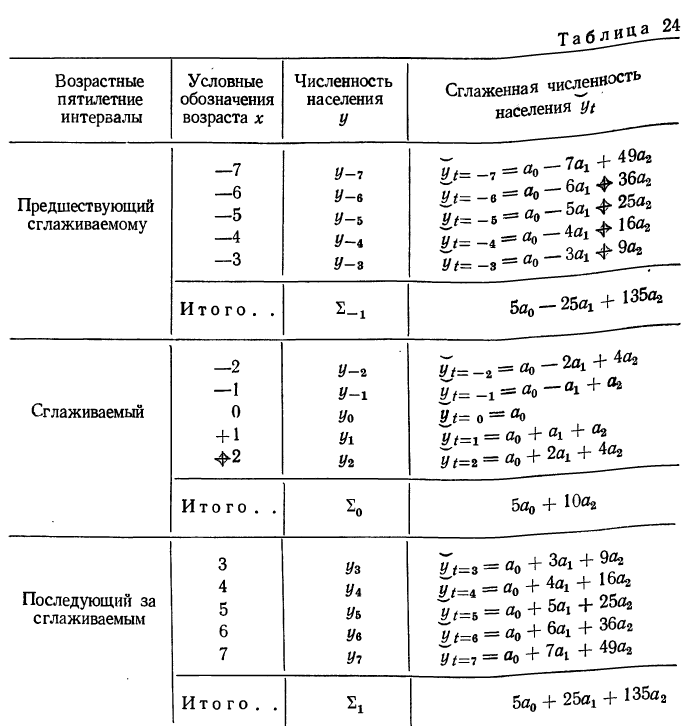
и 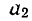 — параметры, определяемые по суммарной численности населения трех пятилетних интервалов: сглаживаемого и двух примыкающих к нему. Построим таблицу и введем в нее соответствующие обозначения (см. табл. 24).
— параметры, определяемые по суммарной численности населения трех пятилетних интервалов: сглаживаемого и двух примыкающих к нему. Построим таблицу и введем в нее соответствующие обозначения (см. табл. 24).
Получив систему трех уравнений:
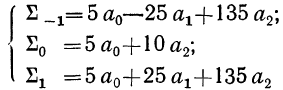
и решая ее относительно параметров 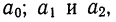 получаем:
получаем: 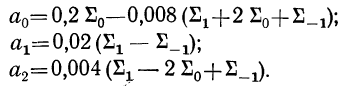
Теперь можно получить сглаженные значения численности каждого годичного интервала:
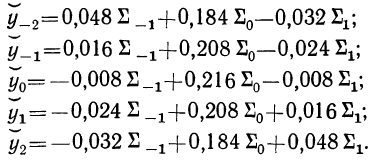
Если нужно произвести интерполяцию и получить сглаженные численности населения каждого годичного интервала из следующего пятилетнего интервала, обозначения соответственно меняются.
Этот метод впервые был применен для устранения аккумуляции возрастного распределения населения по переписи 1897 г.
при построении таблиц смертности 1896—1897 гг. Недостатком данного метода является плохое смыкание парабол соседних пятилетних интервалов.
Пример 15.
Используя данные переписи населения 1897 г. по Европейской России о численности мужчин, произведем интерполяцию возрастного интервала 45—49 лет и найдем сглаженные численности возрастов 45, 46, 47, 48 и 49 лет.

Решение:
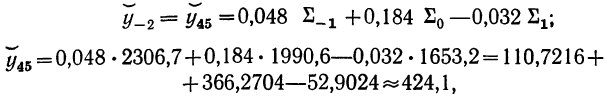
а далее, используя вышеприведенные формулы, получаем: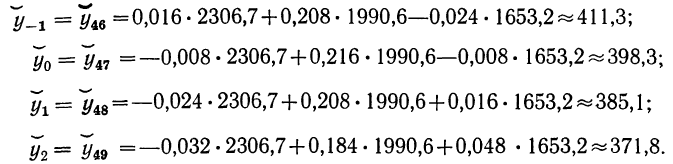
Если сопоставить непосредственные данные, взятые из результатов переписи 1897 г. и искаженные аккумуляцией, со сглаженными, то увидим, что сумма фактических сглаженных данных по пятилетнему интервалу совпадает.
2) Способ Б. С. Ястремского, основанный на применении парабол третьего порядка, позволяет лучше смыкать соседние интервалы.
Имеем:
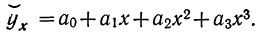
Для нахождения четырех параметров 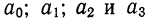 привлекают 4 десятилетних интервала, каждая смежная пара которых имеет по одному общему пятилетнему интервалу. Решая задачу в общем виде и привлекая численности населения еще двух пятилетних интервалов, примыкающих к тем, которые были использованы при способе С. А. Новосельского, т. е.
привлекают 4 десятилетних интервала, каждая смежная пара которых имеет по одному общему пятилетнему интервалу. Решая задачу в общем виде и привлекая численности населения еще двух пятилетних интервалов, примыкающих к тем, которые были использованы при способе С. А. Новосельского, т. е. 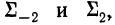 Б. С. Ястремский получил следующую систему уравнений (сохраняем взятую символику):
Б. С. Ястремский получил следующую систему уравнений (сохраняем взятую символику):
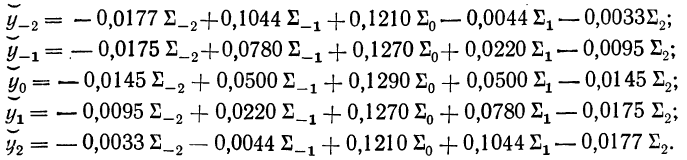
Пример 16.
Используя данные предыдущего примера о численности мужского населения по переписи 1897 г. для трех пятилетних интервалов и привлекая дополнительно данные о численности населения в пятилетних интервалах 35—39 и 55—59 лет, произведем интерполяцию пятилетнего интервала 45—49 лет.

Подставляем и получаем:
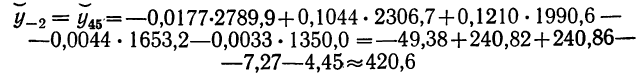
и далее аналогично для всех последующих возрастов.
Метод Б. С. Ястремского применялся при разработке материалов переписи 1920 г.
Экстраполяцией называется нахождение последующих уровней динамического ряда, когда предыдущие уровни известны, Для этой цели может быть использовано выравнивание уровней динамического ряда по способу наименьших квадратов и подстановка в полученное аналитическое уравнение соответствующих значений t.
Так, например, если мы, выравнивая уровни какого-нибудь ряда по параболе второго порядка, с 1956 по 1962 г., получили аналитическое уравнение 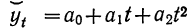 и если у нас есть основания предполагать, что в 1963 и 1964 гг. данная тенденция не изменится, то, подставив в аналитическое уравнение значения t, равные 8 и 9, получим предполагаемые уровни.
и если у нас есть основания предполагать, что в 1963 и 1964 гг. данная тенденция не изменится, то, подставив в аналитическое уравнение значения t, равные 8 и 9, получим предполагаемые уровни.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |