
Статистические оценки - определение и вычисление с примерами решения
Содержание:
Оценки и методы их получения:
Приближенные значения параметров, входящих в законы распределения, определяемые каким-либо способом по выборкам, называются оценками или статистиками. Оценки бывают точечными и интервальными. Точечные оценки представляются одним числом, интервальные - двумя числами 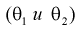
Метод моментов
Пусть генеральная случайная величина X имеет плотность распределения 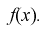
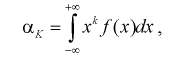 (8.1)
(8.1)
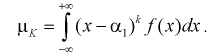 (8.2)
(8.2)
По выборке 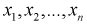 определяем выборочные начальные и центральные моменты:
определяем выборочные начальные и центральные моменты:
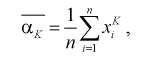 (8.3)
(8.3)
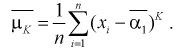 (8.4 )
(8.4 )
Метод моментов состоит в том, что генеральные моменты (8.1, 8.2), в которые входят оцениваемые параметры, приблизительно приравниваются к соответствующим выборочным моментам (8.3), (8.4). Составляется система уравнений:
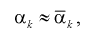 (8.5)
(8.5)
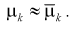 (8.6)
(8.6)
Решая систему (8.5), (8.6), находим оцениваемые параметры.
Особо важную роль играет 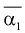 - выборочный начальный момент 1-го по рядка, он называется выборочным средним и обозначается
- выборочный начальный момент 1-го по рядка, он называется выборочным средним и обозначается 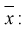
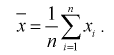 (8.7)
(8.7)
Следующим по важности выборочным моментом является выборочный центральный момент 2-го порядка 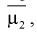 который называется выборочной дисперсией и обозначается
который называется выборочной дисперсией и обозначается 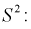
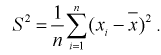 (8.8)
(8.8)
Наиболее часто используются две формулы метода моментов.
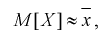 (8.9)
(8.9)
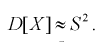 (8.10)
(8.10)
Сформулируем метод моментов в общем виде.
Пусть 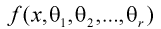 плотность распределения случайной величины
плотность распределения случайной величины 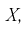 где
где 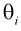 - неизвестные параметры. Чтобы найти оценки
- неизвестные параметры. Чтобы найти оценки 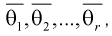 выражаем первые
выражаем первые 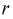 начальных или центральных моментов случайной величины X через параметры
начальных или центральных моментов случайной величины X через параметры 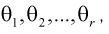 затем генеральные моменты аппроксимируем соответствующими выборочными. В результате имеем систему из
затем генеральные моменты аппроксимируем соответствующими выборочными. В результате имеем систему из 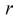 уравнений с
уравнений с 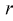 неизвестными, откуда и получаем
неизвестными, откуда и получаем 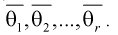
Пример:
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 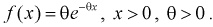 По выборке
По выборке 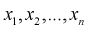 методом моментов найти оценку параметра
методом моментов найти оценку параметра 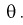
1. Определяем 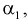 используя (8.1):
используя (8.1):
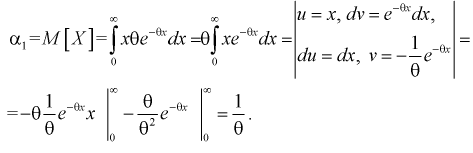
2. По (8.3) или (8.7) находим выборочный начальный момент 1-го порядка или 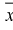 и составляем выражение вида (8.5) или (8.9):
и составляем выражение вида (8.5) или (8.9):
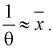
3. Заменяя в п. 2 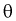 на оценку
на оценку 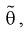 составим уравнение:
составим уравнение: 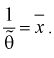
4. Откуда определим оценку параметра 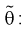
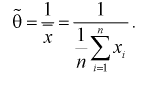
Метод наибольшего правдоподобия
Этот метод предложен математиком Фишером в 1912 г.
Пусть 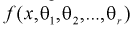 - плотность распределения генеральной случайной величины X, где
- плотность распределения генеральной случайной величины X, где 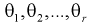 - неизвестные параметры. Согласно методу, наилучшими оценками
- неизвестные параметры. Согласно методу, наилучшими оценками 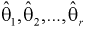 параметров
параметров 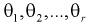 являются такие, для которых функция правдоподобия L принимает наибольшее значение.
являются такие, для которых функция правдоподобия L принимает наибольшее значение.
Для непрерывной случайной величины
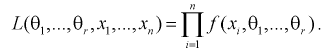 (8.11)
(8.11)
Для дискретной случайной величины
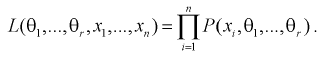 (8.12)
(8.12)
Здесь 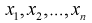 - выборка из генеральной случайной величины X.
- выборка из генеральной случайной величины X.
Априорные выборочные значения 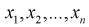 - являются независимыми случайными величинами, закон распределения которых совпадает с законом распределения генеральной случайной величины X. Тогда правую часть (8.11) на основании теоремы умножения законов распределений (см. раздел 3.5) можно рассматривать как плотность распределения вероятности
- являются независимыми случайными величинами, закон распределения которых совпадает с законом распределения генеральной случайной величины X. Тогда правую часть (8.11) на основании теоремы умножения законов распределений (см. раздел 3.5) можно рассматривать как плотность распределения вероятности 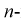 мерного вектора
мерного вектора 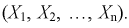 Согласно методу, для наилучших оценок
Согласно методу, для наилучших оценок 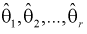 случайный вектор
случайный вектор 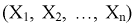 будет иметь наибольшую плотность распределения. То есть надо найти такие оценки
будет иметь наибольшую плотность распределения. То есть надо найти такие оценки 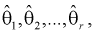 для которых функция правдоподобия L - максимальна. Для этого составляют и решают такую систему уравнений:
для которых функция правдоподобия L - максимальна. Для этого составляют и решают такую систему уравнений:
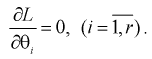 (8.13)
(8.13)
Так как функция и ее логарифм достигают экстремума в одной точке, то часто для упрощения решения задачи используют логарифмическую функцию правдоподобия. В случае логарифмической функции правдоподобия составляется система следующих уравнений:
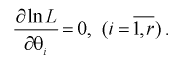 (8.14)
(8.14)
Пример:
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 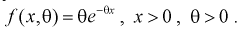 По выборке
По выборке 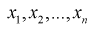 методом наибольшего правдоподобия найти оценку параметра
методом наибольшего правдоподобия найти оценку параметра 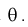
1. Так как нам необходимо оценить один параметр 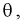 то надо составить и решить одно уравнение. Найдем функцию правдоподобия, используя (8.11):
то надо составить и решить одно уравнение. Найдем функцию правдоподобия, используя (8.11):
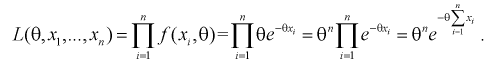
2. Составим логарифмическую функцию правдоподобия:
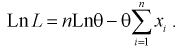
3. Для определения максимума логарифмической функции правдоподобия составляем и решаем следующее уравнение:
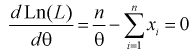
Откуда оценка 0 параметра 0 определяется так:
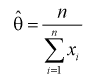
При сравнение это выражение с оценкой 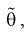 полученной по методу моментов (см. раздел 8.1), мы понимаем, что они одинаковы. Методы, рассмотренные нами, как видим, абсолютно разные. Это свидетельствует о их достоверности.
полученной по методу моментов (см. раздел 8.1), мы понимаем, что они одинаковы. Методы, рассмотренные нами, как видим, абсолютно разные. Это свидетельствует о их достоверности.
Свойства оценок
Пусть 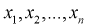 - выборка из генеральной совокупности. Обозначим оценку параметра
- выборка из генеральной совокупности. Обозначим оценку параметра 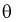 через
через 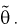 Ранее мы показали, что эта оценка определяется с помощью различных методов по полученной выборке , т. е. являляется функцией от
Ранее мы показали, что эта оценка определяется с помощью различных методов по полученной выборке , т. е. являляется функцией от 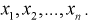
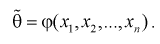
Так как любая выборка типа 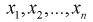 - случайна, то и выборочные функции
- случайна, то и выборочные функции 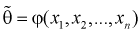 - тоже являются случайными. Следовательно, она тоже имеет свои характеристики.
- тоже являются случайными. Следовательно, она тоже имеет свои характеристики.
1. Оценка 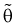 называется несмещенной, если ее математическое ожидание совпадает с самим оцениваемым параметром:
называется несмещенной, если ее математическое ожидание совпадает с самим оцениваемым параметром:
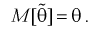
В противном случае оценка называется смещенной.
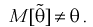
Полную погрешность 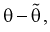 возникшую от замены 0 на 0, можно представить так:
возникшую от замены 0 на 0, можно представить так:
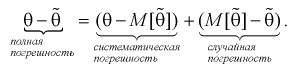
Таким образом, если оценка несмещенная, то систематическая погрешность равна нулю, т. е. 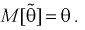
Наиболее опасна систематическая ошибка, если она заранее неизвестна или среднее квадратичное отклонение не очень большое. Среднее значение случайной ошибки 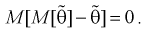
Мы уже отмечали, что 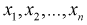 - независимые случайные величины, имеющие тот же закон распределения, что и
- независимые случайные величины, имеющие тот же закон распределения, что и 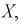 генеральная случайная величина, в частности, выборочное математическое ожидание и дисперсия имеет те же числовые характеристики, т. е. справедливы тождества:
генеральная случайная величина, в частности, выборочное математическое ожидание и дисперсия имеет те же числовые характеристики, т. е. справедливы тождества:
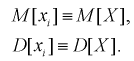 (*)
(*)
Проверим смещенность оценки математического ожидания выборочной средней 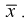 Используя обычные свойства математического ожидания, найдем
Используя обычные свойства математического ожидания, найдем 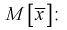
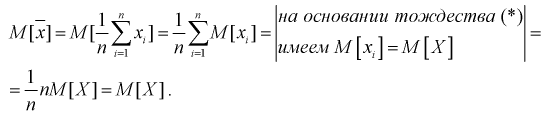
Обозначим 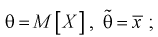 видим, что
видим, что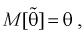 значит, выборочное среднее
значит, выборочное среднее 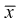 является несмещенной оценкой математического ожидания.
является несмещенной оценкой математического ожидания.
Проверим смещенность оценки дисперсии выборочной дисперсией 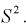 Найдем математическое ожидание от выборочной дисперсии:
Найдем математическое ожидание от выборочной дисперсии:
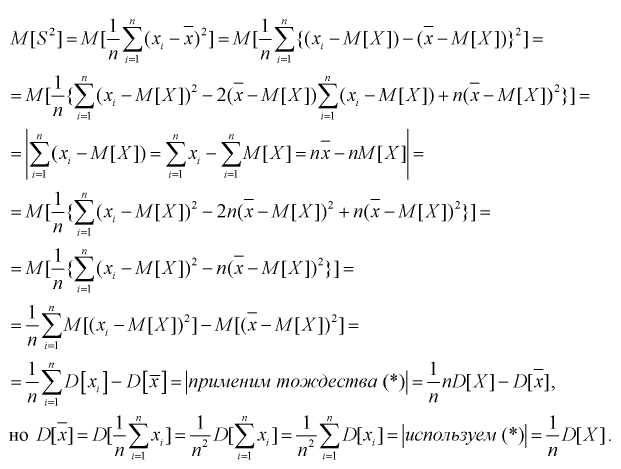
То есть дисперсия выборочной средней в 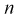 раз меньше дисперсии генеральной случайной величины. Тогда
раз меньше дисперсии генеральной случайной величины. Тогда
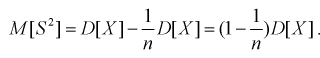
Обозначим 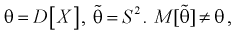 значит, выборочная дисперсия
значит, выборочная дисперсия 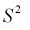 является смещенной оценкой дисперсии. Можно отметить, что выборочная дисперсия
является смещенной оценкой дисперсии. Можно отметить, что выборочная дисперсия 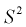 является асимптотически несмещенной оценкой, т. к. при
является асимптотически несмещенной оценкой, т. к. при 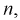 стремящемся к бесконечности, смещение стремится к нулю.
стремящемся к бесконечности, смещение стремится к нулю.
При решении практических задач часто используется несмещенная оценка дисперсии - это модифицированная выборочная дисперсия:
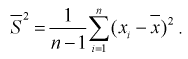
Найдем математическое ожидание от 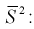
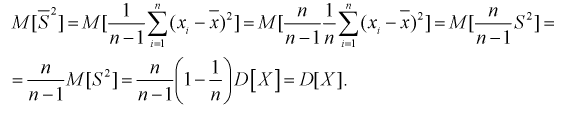
Обозначим 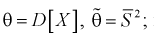 как видим,
как видим, 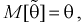 значит, оценка
значит, оценка 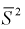 уже несмещенная. При малых
уже несмещенная. При малых 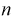 этой формулой пользоваться лучше (при и > 30 оценки совпадают). На практике используют еще одну несмещенную оценку дисперсии - когда известно математическое ожидание:
этой формулой пользоваться лучше (при и > 30 оценки совпадают). На практике используют еще одну несмещенную оценку дисперсии - когда известно математическое ожидание:
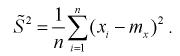
Найдем 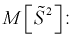
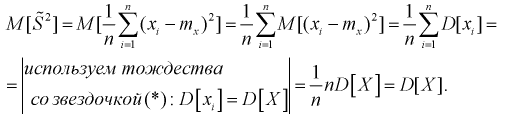
Обозначим 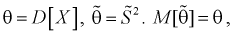 значит, оценка
значит, оценка 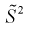 несмещенная.
несмещенная.
2. Оценка 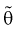 параметра
параметра 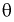 называется состоятельной, если она сходится по вероятности к параметру
называется состоятельной, если она сходится по вероятности к параметру 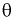 , т. е. если
, т. е. если 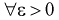 выполняется:
выполняется:
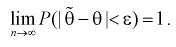
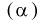
Условие 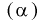 на практике проверить трудно. Поэтому для проверки состоятельности оценок применяют более простые условия:
на практике проверить трудно. Поэтому для проверки состоятельности оценок применяют более простые условия:
а) 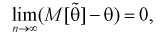
б) 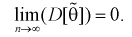
Как видим, оценка 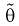 будет состоятельной, если при
будет состоятельной, если при 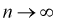 смещение устраняется и дисперсия оценки стремится к нулю.
смещение устраняется и дисперсия оценки стремится к нулю.
Пример:
Проверим состоятельность оценки математического ожидания выборочной средней 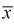 . Ранее мы показали, что
. Ранее мы показали, что 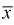 является несмещенной оценкой математического ожидания, т. е. условие а) выполняется и без вычисления предела. Проверим условие б), найдем
является несмещенной оценкой математического ожидания, т. е. условие а) выполняется и без вычисления предела. Проверим условие б), найдем 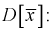
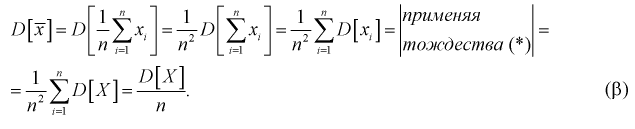
Видим, что при 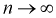 предел
предел 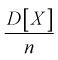 будет стремиться к нулю, значит условие б) выполняется. Следовательно,
будет стремиться к нулю, значит условие б) выполняется. Следовательно, 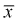 является состоятельной оценкой математического ожидания.
является состоятельной оценкой математического ожидания.
3. Несмещенная оценка 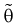 параметра
параметра 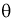 называется эффективной, если она имеет наименьшую дисперсию среди всех оценок при одном и том же объеме выборки
называется эффективной, если она имеет наименьшую дисперсию среди всех оценок при одном и том же объеме выборки 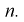
Для определения наименьшей дисперсии эффективной оценки 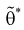 параметра
параметра 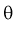 применяется формула Рао-Крамера:
применяется формула Рао-Крамера:
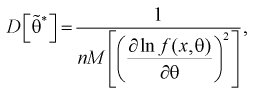 (8.15)
(8.15)
где 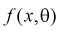 - плотность распределения генеральной случайной величины X.
- плотность распределения генеральной случайной величины X.
Отметим, если оценка 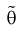 смещенная, то малость ее дисперсии еще не говорит о ее эффективности. Например, если в качестве оценки
смещенная, то малость ее дисперсии еще не говорит о ее эффективности. Например, если в качестве оценки 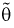 взять любую постоянную величину с, то ее дисперсия будет равна нулю, а ошибка может быть какой угодно большой.
взять любую постоянную величину с, то ее дисперсия будет равна нулю, а ошибка может быть какой угодно большой.
Пример:
Задана нормальная случайная величина 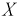 с плотностью распределения
с плотностью распределения
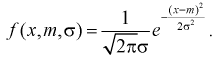
Проверим эффективность оценки математического ожидания выборочной средней 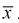 .
.
Найдем дисперсию эффективной оценки параметра 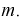 Обозначим эффективную оценку
Обозначим эффективную оценку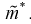 Чтобы воспользоваться формулой Рао-Крамера (8.15), вычислим
Чтобы воспользоваться формулой Рао-Крамера (8.15), вычислим
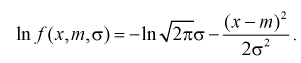
Найдем производную:
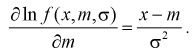
Подставим полученное выражение в (8.15):
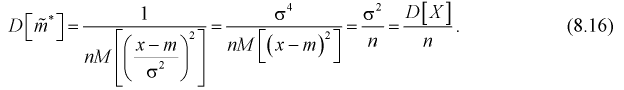
Ранее мы показали, что такую же дисперсию имеет 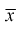 (см. формулу
(см. формулу 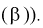
Видим, что правые части формул (8.16) и 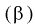 совпадают, следовательно, выборочное среднее
совпадают, следовательно, выборочное среднее 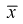 является эффективной оценкой параметра
является эффективной оценкой параметра 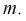
Отметим, что оценки, полученные методом наибольшего правдоподобия, являются состоятельными. Если существуют эффективная оценка, то метод наибольшего правдоподобия позволяет найти ее, но не всегда оценки, полученные этим методом, являются несмещенными.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |