
Геометрические вероятности - определение и вычисление с примерами решения
Геометрические вероятности:
Область применения классического определения вероятности – испытания с конечным числом равновозможных исходов. Существенным является условие равновозможности. От конечности числа исходов опыта можно отказаться и определять вероятности не с помощью числа исходов, 27 а с помощью отношения длин, площадей и т.д., но при сохранении условия равновозможности.
Геометрическое определение вероятности
Пусть область 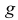
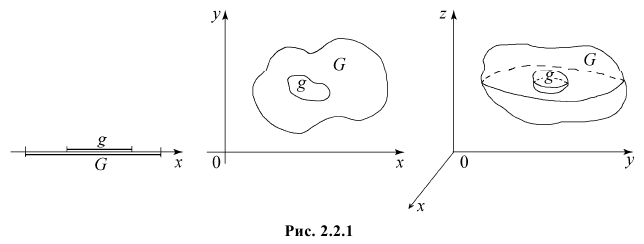
Если равновозможно попадание точки в любую точку области G, то вероятность попасть в область 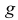 равна отношению меры области
равна отношению меры области 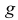 к мере области G:
к мере области G:
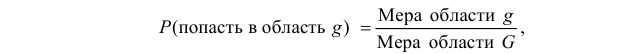
где «мера» – означает: 1) длину, если область G часть прямой или кривой линии; 2) площадь, если G часть плоскости; 3) объем, если G часть пространства, и т.д. в зависимости от характера области G.
Пример:
Две радиостанции течение часа независимо друг от друга должны передать сообщения длительностью 10 мин. и 20 мин. соответственно. Какова вероятность того, что сообщения не перекроются по времени.
Решение. Пусть 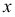 – момент начала сообщения первой радиостанции, а
– момент начала сообщения первой радиостанции, а 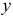 – момент начала второго сообщения. Для того чтобы сообщения уложились в отведенный час, должны выполняться условия:
– момент начала второго сообщения. Для того чтобы сообщения уложились в отведенный час, должны выполняться условия: 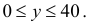 Сообщения не перекроются во времени, если выполнятся условия:
Сообщения не перекроются во времени, если выполнятся условия: 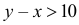 и у
и у 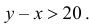 Этим условиям удовлетворяют точки заштрихованных областей, изображенных на рис. 2.2.2.
Этим условиям удовлетворяют точки заштрихованных областей, изображенных на рис. 2.2.2.
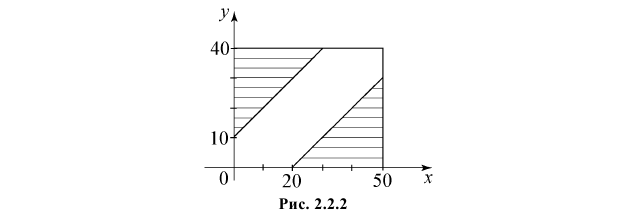
Так как все положения точки 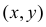 в прямоугольнике
в прямоугольнике 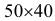 равновозможны, то искомая вероятность равна отношению заштрихованной площади, которая равна
равновозможны, то искомая вероятность равна отношению заштрихованной площади, которая равна 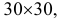 к площади прямоугольника. Поэтому
к площади прямоугольника. Поэтому 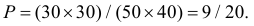
Ответ. 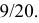
Пример:
В треугольник с вершинами A(0;0), B(4;0) и C(0;2) наугад брошена точка, причем все положения точки в этом треугольнике равновозможны. Найдите вероятность того, что координаты точки X и Y будут удовлетворять неравенству 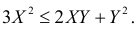
Решение. Полагая в квадратном трехчлене 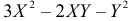 переменной величиной X, а Y коэффициентом, найдем корни трехчлена X=Y и
переменной величиной X, а Y коэффициентом, найдем корни трехчлена X=Y и 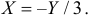 Тогда неравенство
Тогда неравенство 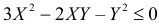 можно записать в виде
можно записать в виде 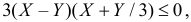 или
или 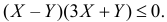 Последнее неравенство равносильно совокупности неравенств:
Последнее неравенство равносильно совокупности неравенств:
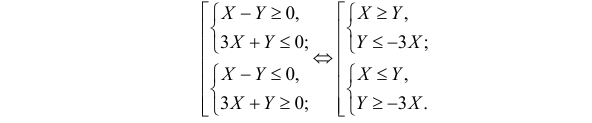
Точки плоскости, координаты которых удовлетворяют этой совокупности систем неравенств, на рис. 2.2.3 выделены штриховкой. Часть из них содержится в треугольнике ABC.
Так как по условию все положения точки 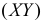 в треугольнике ABC равновозможны, то по геометрическому определению вероятности искомая вероятность равна отношению площади заштрихованного треугольника AEC к площади треугольника ABC.
в треугольнике ABC равновозможны, то по геометрическому определению вероятности искомая вероятность равна отношению площади заштрихованного треугольника AEC к площади треугольника ABC.
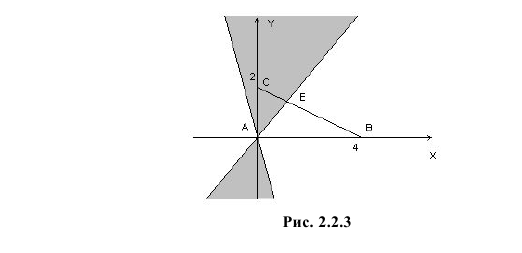
Площадь треугольника ABC равна половине произведения AB на AC, т.е. равна 4. Линия BC имеет уравнение 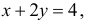 а линия AE определяется уравнением
а линия AE определяется уравнением 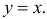
Их точка пересечения имеет координаты E(4/3;4/3). Абсцисса точки E равна высоте треугольника AEC, опущенной на сторону AC. Поэтому площадь треугольника AEC равна 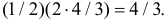 Поэтому искомая вероятность равна
Поэтому искомая вероятность равна 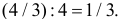
Ответ. 1/3.
Пример:
Координаты случайной точки 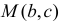 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 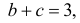 служат коэффициентами квадратного уравнения
служат коэффициентами квадратного уравнения 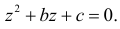 Полагая все положения случайной точки в указанном треугольнике равновозможными, найти вероятность того, что уравнение имеет два действительных корня.
Полагая все положения случайной точки в указанном треугольнике равновозможными, найти вероятность того, что уравнение имеет два действительных корня.
Решение. Пусть А – интересующее нас событие. Уравнение имеет действительные корни, если его дискриминант 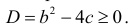 Это неравенство будет выполнено, если случайная точка М попадет в треугольнике ниже кривой
Это неравенство будет выполнено, если случайная точка М попадет в треугольнике ниже кривой 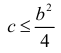 (на рис. 2.2.4 заштрихованная область). Точка пересечения линий
(на рис. 2.2.4 заштрихованная область). Точка пересечения линий 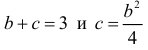 имеет координаты (2;1). Поэтому площадь заштрихованной фигуры на рис. 2.2.4 равна
имеет координаты (2;1). Поэтому площадь заштрихованной фигуры на рис. 2.2.4 равна 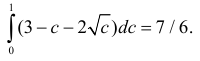
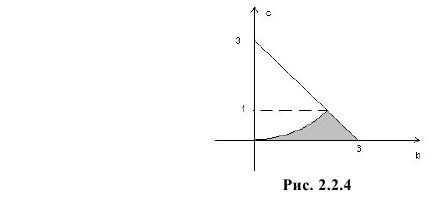
Так как площадь всего треугольника равна 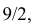 то по геометрическому определению вероятности
то по геометрическому определению вероятности 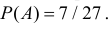
Ответ. 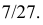
Пример:
Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстояние 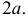 Острый угол ромба равен 60°, а наибольшая диагональ равна
Острый угол ромба равен 60°, а наибольшая диагональ равна 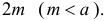 Ромб наугад бросают на плоскость. Какова вероятность того, что ромб пересечет одну из прямых?
Ромб наугад бросают на плоскость. Какова вероятность того, что ромб пересечет одну из прямых?
Решение. Бросание ромба «наугад» подразумевает, что центр ромба с равными шансами может оказаться на любом расстоянии 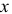 (в пределах от 0 до
(в пределах от 0 до 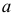 ) от ближайшей прямой, а значения угла
) от ближайшей прямой, а значения угла 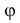 между наибольшей диагональю и ближайшей прямой равновозможны в пределах от
между наибольшей диагональю и ближайшей прямой равновозможны в пределах от 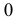 до
до 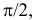 при этом
при этом 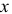 и
и 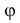 независимы. Заметим, что расстояние от центра ромба до его стороны равно
независимы. Заметим, что расстояние от центра ромба до его стороны равно 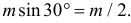
Если 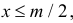 то ромб несомненно пересечет ближайшую прямую. Если же
то ромб несомненно пересечет ближайшую прямую. Если же 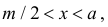 то для пересечения ближайшей прямой необходимо и достаточно, чтобы
то для пересечения ближайшей прямой необходимо и достаточно, чтобы 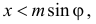 т.е. проекция половины наибольшей диагонали на перпендикуляр к прямой должна быть больше расстояния от центра ромба до прямой (см. рис. 2.2.5).
т.е. проекция половины наибольшей диагонали на перпендикуляр к прямой должна быть больше расстояния от центра ромба до прямой (см. рис. 2.2.5).
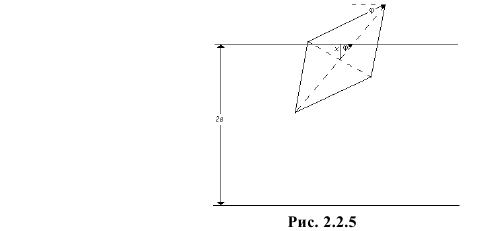
Названные условия выполняются в заштрихованной области на рис. 2.2.6. Графики функций 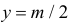 и
и 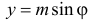 пересекаются в точках, в которых
пересекаются в точках, в которых 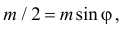 т.е. при
т.е. при 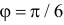 и
и 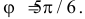 Поэтому заштрихованная площадь равна
Поэтому заштрихованная площадь равна
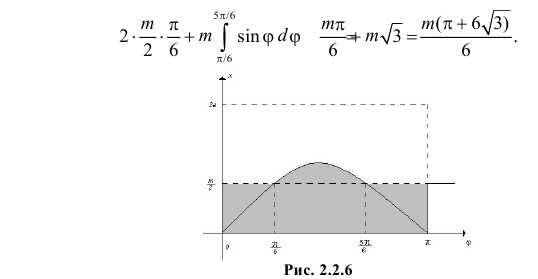
Любое положение ромба относительно ближайшей прямой можно охарактеризовать точкой в прямоугольнике со сторонами 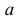 и
и 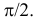 Поскольку все положения ромба относительно ближайшей прямой равновозможны, то по геометрическому определению вероятности искомая вероятность равна
Поскольку все положения ромба относительно ближайшей прямой равновозможны, то по геометрическому определению вероятности искомая вероятность равна 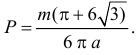
Ответ. 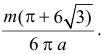
Пример:
Наудачу взяты два положительных числах 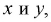 причем
причем 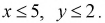 Найти вероятность того, что
Найти вероятность того, что 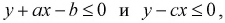 если
если 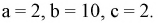
Подставляя значения коэффициентов в неравенства, получаем
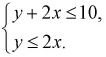
Строим на рис. 1.8 оси координат и область, которая определяет пространство элементарных событий 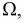 она задается неравенствами
она задается неравенствами 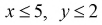 и отображается на рисунке 1.8 прямоугольником.
и отображается на рисунке 1.8 прямоугольником.
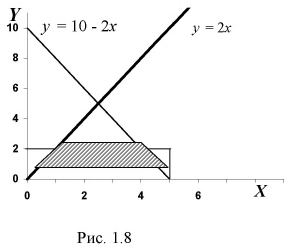
Площадь прямоугольника 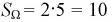 [условных единиц]. Область благоприятствующих исходов определяется неравенствами
[условных единиц]. Область благоприятствующих исходов определяется неравенствами  поэтому строим на рисунке прямые, которые задаются из неравенств
поэтому строим на рисунке прямые, которые задаются из неравенств  Заштрихованная на рисунке 1.8 область описывает благоприятствующие исходы (с учетом всех возможных значений) и является трапецией, площадь которой
Заштрихованная на рисунке 1.8 область описывает благоприятствующие исходы (с учетом всех возможных значений) и является трапецией, площадь которой 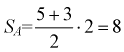 [условных единиц]. Тогда вероятность события
[условных единиц]. Тогда вероятность события 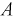
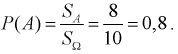
Пример:
Найти вероятность того, что на экране радиолокатора отметка от цели появится в кружке радиусом 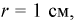 на азимуте
на азимуте 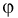 ноль градусов, на расстоянии
ноль градусов, на расстоянии 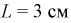 от центра экрана, если радиус экрана равен 30 см.
от центра экрана, если радиус экрана равен 30 см.
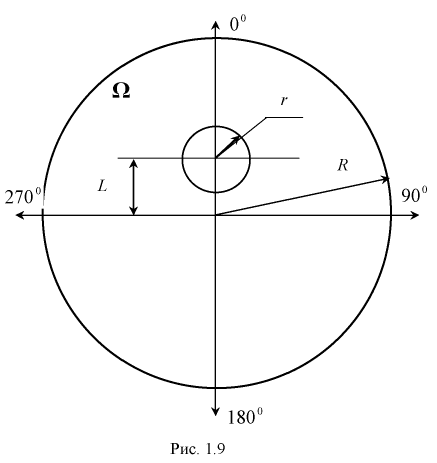
Экран радиолокатора, рис. 1.9, представляет собой электронно-лучевую трубку с радиальной разверткой, в которой от центра до края экрана движется электронный луч и после достижения края движение луча опять начинается от центра к краю, но с некоторым смещением по азимуту. Это перемещение луча от центра экрана соответствует началу излучения радиоимпульса антенного радиолокатора, который укреплен на боковой стенке кабины с передающим устройством, а кабина, в свою очередь, вращается вокруг вертикальной оси, что соответствует смещению луча на экране по азимуту. И когда радиоимпульс отражается от цели, на экране радиолокатора вспыхивает яркая точка. По положению этой точки на экране легко определить расстояние до цели и ее азимут.
Зная геометрическое определение вероятности, можно сразу сказать, что вероятность появления отметки от цели в кружке радиусом 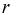 зависит только от отношения площадей и не зависит ни от формы области благоприятствующих исходов, ни от места ее расположения. Поэтому в этой задаче есть избыточная информация - расстояние
зависит только от отношения площадей и не зависит ни от формы области благоприятствующих исходов, ни от места ее расположения. Поэтому в этой задаче есть избыточная информация - расстояние 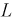 и азимут
и азимут 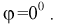
Определяем область благоприятствующих исходов, которой является кружок радиусом 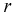 и площадью -
и площадью - 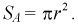 Пространство элементарных событий
Пространство элементарных событий 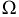 - это область экрана, его площадь
- это область экрана, его площадь 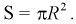 Тогда
Тогда
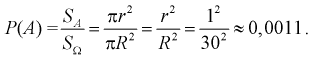
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |