
Перемещение, координата и путь при равнопеременном движении в физике с примерами
Перемещение, координата и путь при равнопеременном движении:
Мы знаем, что при равнопеременном движении скорость тела линейно зависит от времени. А как зависит от времени перемещение? Координата? Пройденный путь?
В предыдущем параграфе для равнопеременного движения была найдена зависимость проекции скорости от времени:

и получена формула для проекции перемещения:

Подставляя 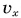 из равенства (1) в (2), находим зависимость проекции перемещения от времени:
из равенства (1) в (2), находим зависимость проекции перемещения от времени:

Отметим, что при движении с постоянным ускорением соотношения (1) и (3) выполняются и для векторов скорости и перемещения:
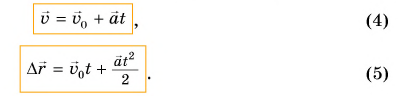
Учитывая, что проекция перемещения 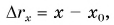 из формулы (3) находим координату:
из формулы (3) находим координату:

Формула (6) выражает кинематический закон равнопеременного движения. Функции (3) и (6) называются квадратичными. Следовательно, при равнопеременном движении проекция перемещения тела и его координата квадратично зависят от времени.
Сравним зависимости основных кинематических величин от времени для двух видов прямолинейного движения: равномерного и равнопеременного (табл. 1).
Таблица 1

Из таблицы видно, что при 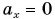 формулы равнопеременного движения переходят в формулы равномерного.
формулы равнопеременного движения переходят в формулы равномерного.
Рассмотрим графики проекций 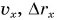 и координаты х на конкретном примере: три тела (0, 1 и 2) движутся вдоль оси Ох. Их начальные скорости одинаковы
и координаты х на конкретном примере: три тела (0, 1 и 2) движутся вдоль оси Ох. Их начальные скорости одинаковы 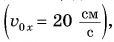 проекции ускорения различны:
проекции ускорения различны: 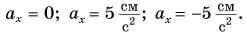
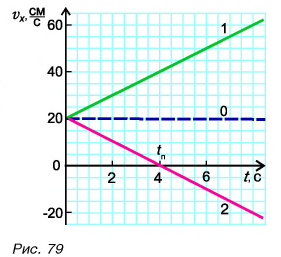
По формуле (1) 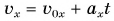 построим графики проекции скорости этих тел (графики 0, 1, 2 на рис. 79). Графики прямолинейны, а их наклон определяется значением проекции ускорения
построим графики проекции скорости этих тел (графики 0, 1, 2 на рис. 79). Графики прямолинейны, а их наклон определяется значением проекции ускорения 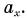 График 2 пересекает ось времени в момент поворота
График 2 пересекает ось времени в момент поворота 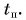
Перейдем к графикам проекции перемещения 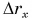 (рис. 80).
(рис. 80).
Как мы знаем, при 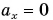 (т. е. для равномерного движения)
(т. е. для равномерного движения) 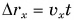 и график
и график 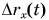 — наклонная прямая линия (график
— наклонная прямая линия (график 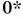 на рис. 80).
на рис. 80).
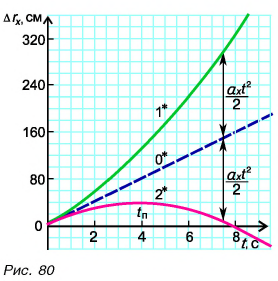
Из таблицы 1 видно, что формулы для проекции перемещения 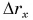 при равномерном и равнопеременном движениях отличаются только на слагаемое
при равномерном и равнопеременном движениях отличаются только на слагаемое 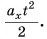 Поэтому при
Поэтому при 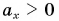 точки графика 0* для каждого значения t следует поднять на
точки графика 0* для каждого значения t следует поднять на 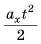 (график 1*), а при
(график 1*), а при 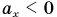 (график 2*) — настолько же опустить (рис. 80).
(график 2*) — настолько же опустить (рис. 80).
Так как 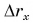 квадратично зависит от времени (см. формулу (3)), графики проекции перемещения при равнопеременном движении являются участками парабол (рис. 80).
квадратично зависит от времени (см. формулу (3)), графики проекции перемещения при равнопеременном движении являются участками парабол (рис. 80).
Обратите внимание на поведение графиков 2 и 2* в момент поворота 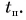 График 2 для
График 2 для 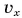 (рис. 79) в этот момент проходит через нуль, а график 2* для
(рис. 79) в этот момент проходит через нуль, а график 2* для 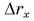 (рис. 80) при
(рис. 80) при 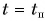 достигает максимума, а затем начинает опускаться. Графики подтверждают: в момент поворота направление движения тела изменяется на противоположное.
достигает максимума, а затем начинает опускаться. Графики подтверждают: в момент поворота направление движения тела изменяется на противоположное.
А каким будет график пути? Для движения, при котором направление скорости не изменяется, график пути 1б (рис. 81) совпадает с графиком проекции перемещения 1а. Если же скорость меняет свое направление, то график пути s (2б) и график проекции перемещения 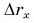 (2а) будут совпадать лишь до момента поворота
(2а) будут совпадать лишь до момента поворота 
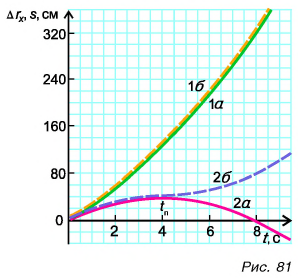
При 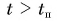 проекция перемещения
проекция перемещения 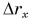 начинает уменьшаться, а путь s продолжает расти. Он увеличивается на столько, на сколько за то же время уменьшается проекция перемещения.
начинает уменьшаться, а путь s продолжает расти. Он увеличивается на столько, на сколько за то же время уменьшается проекция перемещения.
От графика проекции перемещения 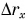 легко перейти к графику координаты х (рис. 82).
легко перейти к графику координаты х (рис. 82).
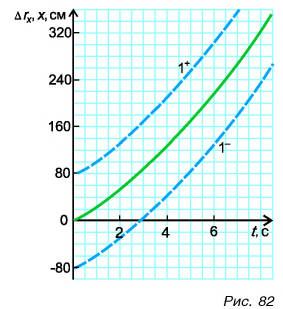
Так как, согласно формуле (6), 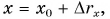 то графики координаты х (параболы
то графики координаты х (параболы 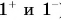 ) получаются путем смещения графика
) получаются путем смещения графика 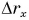 на величину
на величину 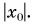 Смещение вверх происходит при
Смещение вверх происходит при 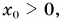 а вниз — при
а вниз — при 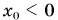 (рис. 82). Выведем еще две формулы, полезные для решения задач о равнопеременном движении.
(рис. 82). Выведем еще две формулы, полезные для решения задач о равнопеременном движении.
Выразим время из формулы проекции скорости (1): 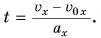 Подставив это выражение в формулу (2), получим:
Подставив это выражение в формулу (2), получим: 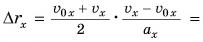
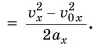 Следовательно, при равнопеременном движении
Следовательно, при равнопеременном движении

В случае когда начальная скорость и ускорение одинаково направлены, из равенства (7) следует:

где s — пройденный путь.
Главные выводы:
- При равнопеременном движении тела его перемещение и координата — квадратичные функции времени.
- Графики зависимости проекции перемещения и координаты от времени для равнопеременного движения являются участками парабол.
- Вершина параболы на графике проекции перемещения соответствует моменту времени, при котором мгновенная скорость равна нулю.
Пример решения задачи:
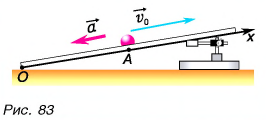
Шарику, находящемуся в точке А, расположенной посередине наклонного желоба длиной 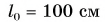 (рис. 83), сообщили начальную скорость
(рис. 83), сообщили начальную скорость 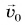 вдоль наклонного желоба вверх. Ускорение шарика
вдоль наклонного желоба вверх. Ускорение шарика 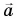 направлено вдоль желоба вниз. Найдите координату точки поворота
направлено вдоль желоба вниз. Найдите координату точки поворота 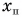 и время
и время 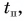 за которое шарик ее достигнет, если
за которое шарик ее достигнет, если
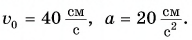
Определите время, когда шарик вернется в точку А, и время, когда он окажется в точке О. Постройте графики проекций скорости и перемещения, а также координаты шарика.
Пример решения задачи:

Решение
Выберем ось Ох, как показано на рисунке 83. Тогда проекция скорости 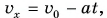 проекция перемещения
проекция перемещения 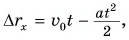 координата
координата 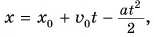 где
где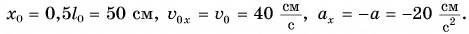
По этим формулам для моментов времени 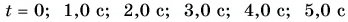 найдем значения
найдем значения 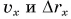 и занесем результаты в таблицу.
и занесем результаты в таблицу.
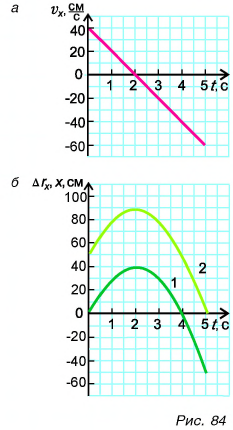
Используя полученные значения, строим графики проекций скорости (рис. 84, а) и перемещения (рис. 84, б, график 1) за промежуток времени от 0 до 5 с.
График координаты получим, сдвинув график проекции перемещения на 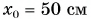 вверх (график 2 на рис. 84, б). Из графиков и таблицы находим: координата точки поворота
вверх (график 2 на рис. 84, б). Из графиков и таблицы находим: координата точки поворота 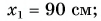 шарик достиг ее в момент
шарик достиг ее в момент 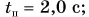 в точке А шарик оказался при
в точке А шарик оказался при 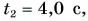 а в точке О — при
а в точке О — при 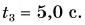
Ответ: 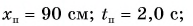
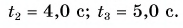
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |