Дана выборка из значений индекса EV/Net Income (показатель, который сравнивает стоимость предприятия с его чистой

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16423
		Прошла проверку преподавателем МГУ
		245 руб.

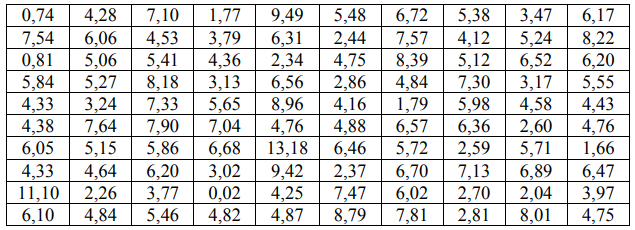
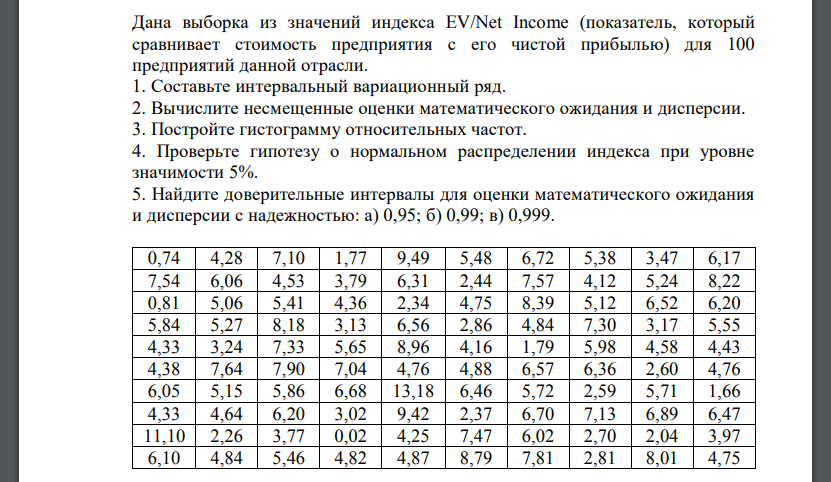
Дана выборка из значений индекса EV/Net Income (показатель, который сравнивает стоимость предприятия с его чистой прибылью) для 100 предприятий данной отрасли. 1. Составьте интервальный вариационный ряд. 2. Вычислите несмещенные оценки математического ожидания и дисперсии. 3. Постройте гистограмму относительных частот. 4. Проверьте гипотезу о нормальном распределении индекса при уровне значимости 5%. 5. Найдите доверительные интервалы для оценки математического ожидания и дисперсии с надежностью: а) 0,95; б) 0,99; в) 0,999.

Решение

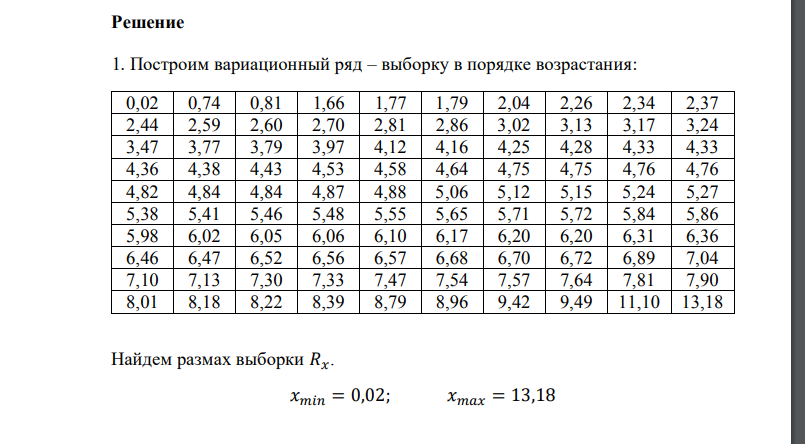
1. Построим вариационный ряд – выборку в порядке возрастания: Найдем размах выборки  Число интервалов 𝑁, на которые следует разбить интервал значений признака, найдём по формуле Стерджесса:  где n − объём выборки, то есть число единиц наблюдения. В данном случае . Получим: Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Округление шага производится, как правило, в большую сторону. Таким образом, принимаем ℎ = 1,7. За начало первого интервала принимаем такое значение из интервала  чтобы середина полученного интервала оказалась удобным для расчетов числом. В нашем случае за нижнюю границу интервала возьмём 0. Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. Относительные частоты 𝑚∗ определим по формуле: