
Дано вершины i=1,2,3,..23 дуги (i,j), i,j=1,2,3,..23 Длины дуг Lij, i,j=1,2,3,..23 Конечная вершина b=7 Требуется построить кратчайшие пути
 |
 |
Экономика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №17177 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Дано вершины i=1,2,3,..23 дуги (i,j), i,j=1,2,3,..23 Длины дуг Lij, i,j=1,2,3,..23 Конечная вершина b=7 Требуется построить кратчайшие пути от всех вершин до вершины b=7 Таблица 4 – Длины дуг графа
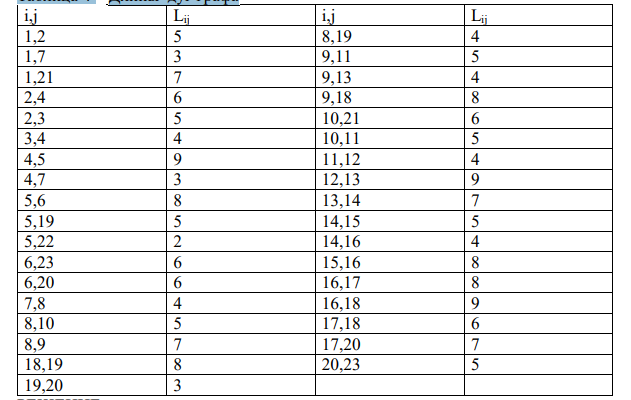
РЕШЕНИЕ
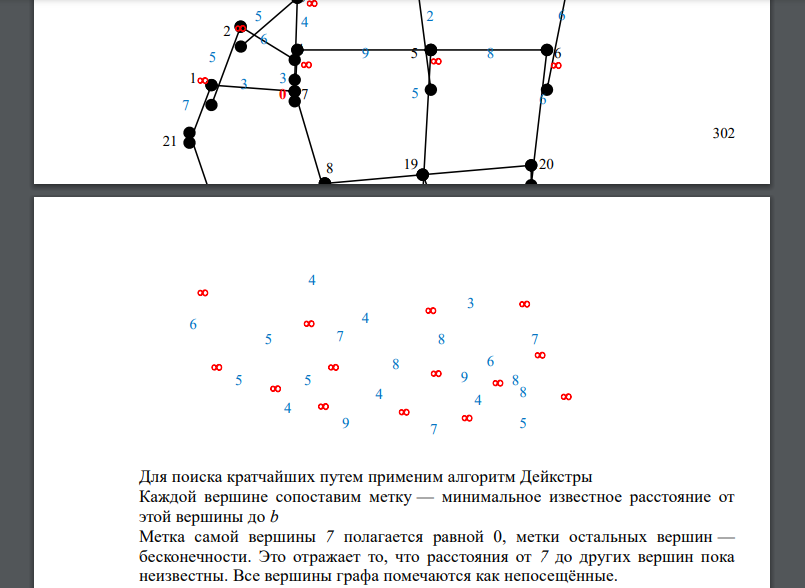
Нанесем на дуги их длины
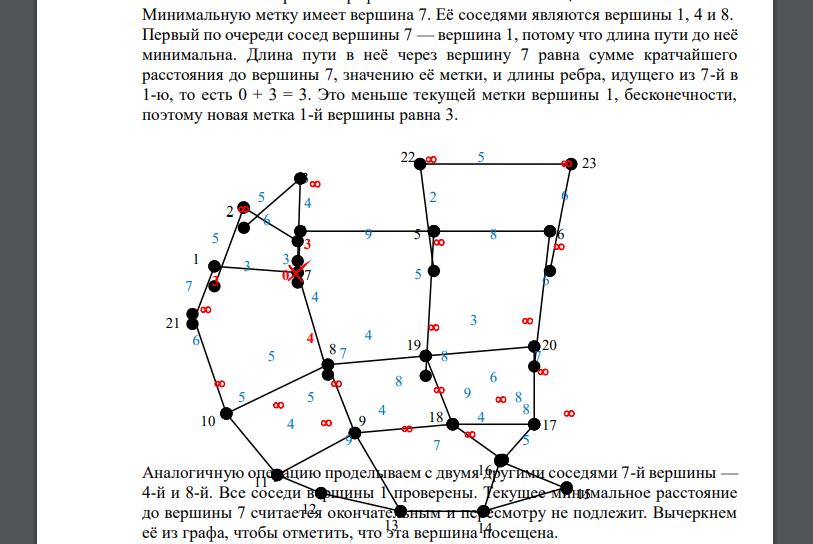
Для поиска кратчайших путем применим алгоритм Дейкстры Каждой вершине сопоставим метку — минимальное известное расстояние от этой вершины до b Метка самой вершины 7 полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от 7 до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые. Минимальную метку имеет вершина 7. Её соседями являются вершины 1, 4 и 8. Первый по очереди сосед вершины 7 — вершина 1, потому что длина пути до неё минимальна. Длина пути в неё через вершину 7 равна сумме кратчайшего расстояния до вершины 7, значению её метки, и длины ребра, идущего из 7-й в 1-ю, то есть 0 + 3 = 3. Это меньше текущей метки вершины 1, бесконечности, поэтому новая метка 1-й вершины равна 3.

Похожие готовые решения по экономике:
- Цель работы: построение самой дешевой из всех возможных сетей дорог, соединяющих города Дано: а) вершина графа
- Сущность и значения статистических методов, применяемых для анализа контроля качества деталей
- Результаты статистического анализа и приемочного контроля качества партии деталей: а) исходные данные
- С помощью функции pridict предскажите поведение функции f(x)=sin(2*x) на отрезке [2π, 4π], если предположить
- Дано I - начальная стоимость вклада в банк и i – годовая процентная ставка Требуется найти будущие стоимости
- Дано I – стоимость инвестиции, r – коэффициент дисконта, Рk=P0(1+pk) – прибыль по годам, k – количество периодов
- Даны значения величин n1=2 года, n2=3 года, n3=1 год, i1=0.1, i2=0.07, i3=0.12, I=350 тыс. руб., Q=3 Требуется найти среднюю годовую
- Даны значения величин S1=350 тыс. руб., S2=360 тыс. руб., S3=340 тыс. руб., n1=3 года, n2=6 лет, n3=2 года, i=0.08 Требуется найти
- Пусть кривая совокупного спроса задана следующим уравнением (AD): Y=А+M/P, где А=120 - константа, М = 200 денежная масса
- Две фирмы А и В могут осуществлять капиталовложения в четыре объекта. Стратегии фирм: стратегия Аi состоит в финансировании фирмой
- Чтобы прибыль сократилась на 100% согласно DOL выручка должна сократиться на 100/3=33,33%
- Покупатель передал в кассу нашей компании 7 000 рублей за партию бумаги

