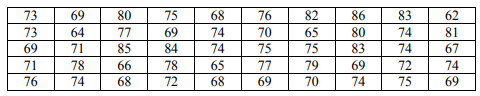
Даны значения признака 𝑋, полученные в результате выборочного обследования совокупности. Требуется: 73 69 80 75 68 76 82 86 83 62 73 64 77 69 74 70 65 80 74 81 69 71 85 84 74 75 75 83 74

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16412
		Прошла проверку преподавателем МГУ
		245 руб.

Даны значения признака 𝑋, полученные в результате выборочного обследования совокупности. Требуется: 1) построить интервальный вариационный ряд частот с равными интервалами, выбрав число интервалов 8 или 9; 2) построить гистограмму частот; 3) построить дискретный вариационный ряд, соответствующий данному интервальному; 4) найти эмпирическую функцию распределения по дискретному ряду; 5) построить график эмпирической функции распределения; 6) вычислить выборочную среднюю, выборочную дисперсию и выборочное среднеквадратическое отклонение; 7) вычислить теоретические частоты по интервальному вариационному ряду выборки, предположив, что случайная величина 𝑋 распределена нормально; 8) используя критерий Пирсона при уровне значимости 𝛼 = 0,01, проверить гипотезу о нормальном распределении случайной величины 𝑋; 9) найти доверительный интервал для оценки математического ожидания с надежностью 𝛾 = 0,99. 

Решение

Построим интервальный вариационный ряд частот с равными интервалами, выбрав число интервалов 8. Построим вариационный ряд – выборку в порядке возрастания:  Найдем размах выборки  Число интервалов 𝑁, на которые следует разбить интервал значений признака, принимаем равным: 𝑁 = 8. Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Подсчитаем частоту 𝑛𝑖 каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. Относительные частоты (частости) 𝑓𝑖 определим по формуле: Построим интервальный вариационный ряд частот с равными интервалами. Интервал Середина интервала Частота  Частость  2) Построим гистограмму частот. 3) Построим дискретный вариационный ряд, соответствующий данному интервальному. 4) Найдем эмпирическую функцию распределения по дискретному ряду.  5) Построим график эмпирической функции распределения. 6) Вычислим выборочную среднюю 𝑥̅, выборочную дисперсию 𝐷в и выборочное среднеквадратическое отклонение  Среднее квадратическое отклонение равно: 7) Вычислим теоретические частоты по интервальному вариационному ряду выборки, предположив, что случайная величина 𝑋 распределена нормально. Исправленная дисперсия: Исправленное среднее квадратическое отклонение равно:  Вероятность попадания случайной величины в каждый интервал равна приращению функции распределения:  Теоретические частоты определим по формуле и вычислим значения  Результаты запишем в таблицу Интервалы  Здесь объединены первые два и последние два интервала, чтобы выполнялось условие. В итоге получили  интервалов, число степеней свободы для 𝜒 2 распределения равно. 8) Используя критерий Пирсона при уровне значимости , проверим гипотезу о нормальном распределении случайной величины 𝑋. Получили. Число степеней свободы нормального распределения 𝑣 = 3. По таблице при уровне значимости  находим. Так как, то нет оснований отвергать гипотезу о нормальном распределении при заданном уровне значимости. 9) Найдем доверительный интервал для оценки математического ожидания с надежностью. Доверительный интервал для математического ожидания a нормально распределенной случайной величины: такое значение аргумента функции Лапласа, при котором. Для  по таблице функции Лапласа находим 𝑡 из равенства:  Получаем, и доверительный интервал имеет вид: