На примере своей задачи охарактеризовать ряд распределения с помощью следующих показателей: 1) Средняя величина

		Экономическая теория
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №17461
		Прошла проверку преподавателем МГУ
		245 руб.

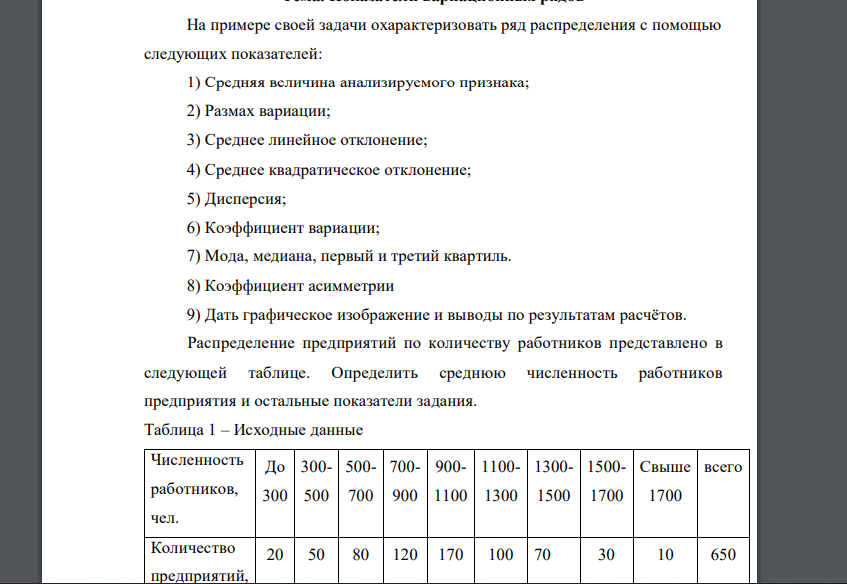
На примере своей задачи охарактеризовать ряд распределения с помощью следующих показателей: 1) Средняя величина анализируемого признака; 2) Размах вариации; 3) Среднее линейное отклонение; 4) Среднее квадратическое отклонение; 5) Дисперсия; 6) Коэффициент вариации; 7) Мода, медиана, первый и третий квартиль. 8) Коэффициент асимметрии 9) Дать графическое изображение и выводы по результатам расчётов. Распределение предприятий по количеству работников представлено в следующей таблице. Определить среднюю численность работников предприятия и остальные показатели задания 

РЕШЕНИЕ

Заменим крайние интервалы на закрытые. Так как ширина остальных интервалов 200, то первый интервал заменим на 100-300, а последний на 1700- 1900 1. Среднюю арифметическую рассчитывают по формуле, где хi- значение осредняемого признака, fi- частота, n- число единиц совокупности.2. Размах вариации представляет собой разность между наибольшим (хmax) и наименьшим (xmin) значениями вариант. 3. Среднее линейное отклонение (d ) определяется из отношения суммы, взятой по абсолютной величине (без учёта знака) отклонения всех вариант от средней арифметической, к объёму всей совокупности.  4. Дисперсия  2 - это средняя из квадратов отклонений значений признака от его средней арифметической величины. Она определяется по формуле. 5. Среднее квадратическое отклонение. 6. Мерой сравнения степеней колеблемости для двух, трех и более вариационных рядов служит показатель, который носит название коэффициента вариации и определятся по формуле. Коэффициент вариации показывает однородность выбранной совокупности: чем он меньше, тем более однородна совокупность. Для однородной совокупности он не превышает 33%. 7. Вычисление моды в интервальном ряду с равными интервалами производится по следующей формуле, где хМо - начало (нижняя граница) модального интервала (700); i - величина интервала (200); fМо - частота модального интервала (170); f Мо-1 - частота интервала, предшествующего модальному (120); f М0+1 - частота интервала, следующего за модальным (100). Воспользуемся данными табл. 2 и рассчитаем моду. Медиана (Ме)- варианта, находящаяся в средине ряда распределения. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Срединная варианта и будет являться медианой. Расчет медианы для интервального ряда производится по формуле, где хМе - начало (нижняя граница) медианного интервала (700); i- величина интервала (200); fi - сумма накопленных частот ряда (650); sМе-1 - накопленная частота вариант, предшествующих медианному (270); fМе - частота медианного интервала (170). Воспользуемся данными табл. 2 и рассчитаем медиану. В табл. 2 Ме приходится на 326-ю частоту, а она находятся в сумме накопленных частот,  равной 440, поэтому интервал 900-1100 является медианным. Определяем медиану. Для характеристики социально-экономического явления, отражённого рядом распределения, следует рассчитать первый и третий квартиль (второй равен медиане) по следующим формулам, аналогичным медиане. 8. Сравнивая среднее значение признака с модой и медианой можно отметить, что их значения довольно близки, но не равны между собой. Следовательно ряд распределения имеет некоторую асимметрию, которая может быть определена по формуле, т.е. коэффициент асимметрии меньше 0, Мо больше среднего значения признака и это говорит о левосторонней асимметрии. 9. Представим ряд графически: Результаты расчета средней и показателей вариации представим в таблице 2. Выводы: по результатам расчетов получили, что средняя численность персонала в исследуемой группе составляет 956,923 чел. Среднее квадратическое отклонение возраста составляет 349,932 чел.. Коэффициент вариации позволяет сделать вывод, что ряд распределения по численности неоднороден. Наиболее типичная численность в исследуемой группе предприятий составляет 983,33 чел. Расчёт квартилей позволяет отметить, что на 25% предприятия численность работников менее 720,833 чел., а на 25% - свыше 1195 чел. Остальные 50% имеют численность от 720,833 до 1195 чел. Ряд распределения имеет левостороннюю асимметрию.