По выборке одномерной случайной величины: - получить вариационный ряд; построить

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16441
		Прошла проверку преподавателем МГУ
		245 руб.

По выборке одномерной случайной величины: - получить вариационный ряд; - построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x); - построить гистограмму равноинтервальным способом; - построить гистограмму равновероятностным способом; - вычислить точечные оценки математического ожидания и дисперсии; - вычислить интервальные оценки математического ожидания и дисперсии (γ= 0,95); - выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия χ2 и критерия Колмогорова (α = 0,05). Одномерная выборка: 0.23 3.23 2.18 0.28 8.60 0.40 2.90 3.90 1.68 1.58 4.37 0.34 0.73 1.34 0.69 4.96 7.06 1.07 0.35 0.23 3.24 1.99 0.46 0.71 0.25 5.41 1.60 1.10 1.75 1.60 0.63 0.72 0.02 2.92 1.17 1.53 1.14 0.34 7.42 0.09 0.39 0.76 0.33 0.82 1.45 2.93 0.97 0.70 0.47 0.96 1.17 3.21 1.58 0.10 3.05 0.76 0.38 0.84 5.68 3.80 2.04 0.83 2.35 1.18 0.96 0.96 0.04 2.78 2.08 0.06 2.70 2.07 2.65 0.92 1.12 1.83 0.10 1.74 2.35 1.56 2.64 2.12 5.28 0.60 1.84 1.51 1.25 2.60 6.44 1.83 1.04 1.99 0.01 0.00 0.68 0.84 0.54 7.54 1.60 8.06

Решение

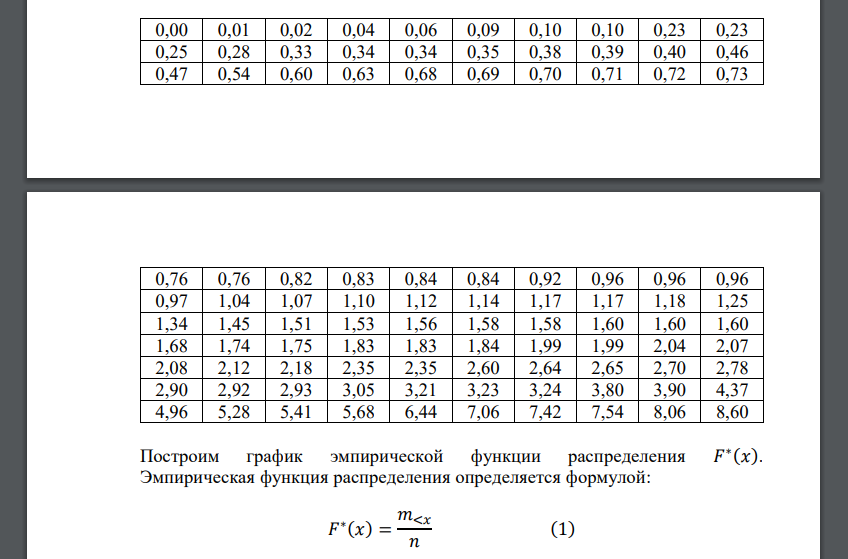
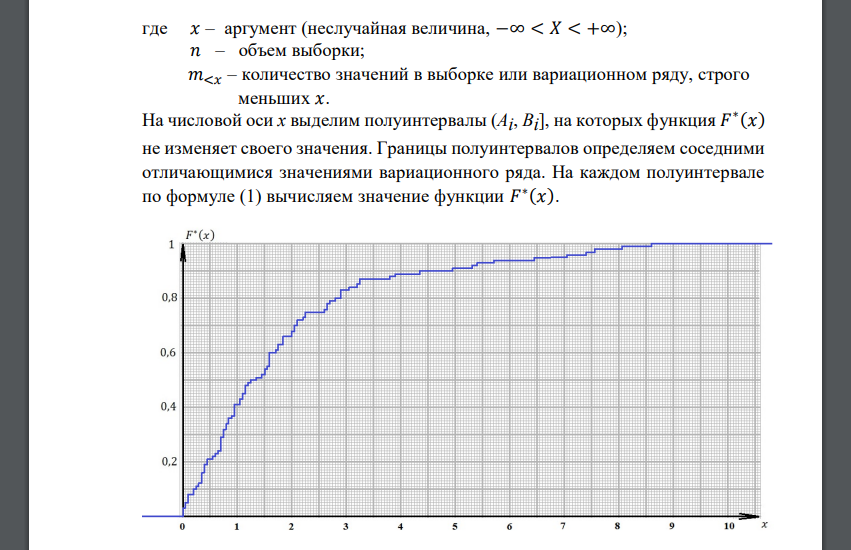
Построим вариационный ряд (выборку в порядке возрастания):  Построим график эмпирической функции распределения 𝐹 ∗ (𝑥). Эмпирическая функция распределения определяется формулой: 𝐹 ∗ (𝑥) = 𝑚<𝑥 𝑛 (1) где 𝑥 – аргумент (неслучайная величина, −∞ < 𝑋 < +∞); 𝑛 – объем выборки; 𝑚<𝑥 – количество значений в выборке или вариационном ряду, строго меньших 𝑥. На числовой оси x выделим полуинтервалы (Ai , Bi ], на которых функция 𝐹 ∗ (𝑥) не изменяет своего значения. Границы полуинтервалов определяем соседними отличающимися значениями вариационного ряда. На каждом полуинтервале по формуле (1) вычисляем значение функции 𝐹 ∗ (𝑥). Построим гистограмму равноинтервальным способом. Шаг: ℎ = 8,60 − 0 √100 = 0,86 Данные интервала, число выборочных значений и среднюю плотность вероятности для каждого интервала сведем в таблицу 1. Среднюю плотность вероятности для каждого интервала вычислим по формуле 𝑓𝑖 = 𝛾𝑖 𝑛 ∙ ℎ Таблица 1. Интервалы Число значений 𝛾𝑖 Плотность вероятности Построим гистограмму Построим гистограмму равновероятностным способом. Определим границы интервалов, в каждом из которых 10 выборочных значений. Данные интервала и среднюю плотность вероятности для каждого интервала сведем в таблицу 2. Среднюю плотность вероятности для каждого интервала вычислим по формуле