Получены данные коэффициента интеллекта 70 взрослых людей. Результаты измерений приведены ниже. 141 115 123 124 121 107 116 123 114 105 104 91 132 118 129

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16412
		Прошла проверку преподавателем МГУ
		245 руб.

Получены данные коэффициента интеллекта 70 взрослых людей. Результаты измерений приведены ниже. 

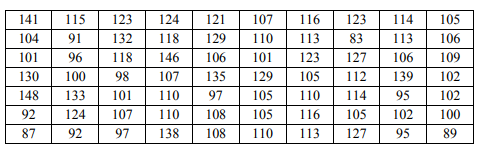
Задание 1. Постройте статистический ряд. Задание 2. Вычислите относительные частоты и накопленные относительные частоты. Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы. Задание 4. Постройте график накопленных относительных частот. Задание 5. Запишите эмпирическую функцию распределения. Задание 6. Вычислите точечные оценки параметров закона распределения: 6) выборочное среднее; 7) выборочную дисперсию (смещённую и несмещённую); 8) выборочное среднее квадратическое отклонение (смещённое и несмещённое); 9) выборочную моду; 10) выборочную медиану. Задание 7. Положим, изучаемая генеральная совокупность подчиняется нормальному закону распределения. Найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна и доверительная вероятность задаётся формулой  = 0,9 + 0,01 𝑖, где i – последняя цифра шифра зачётной книжки.

Решение

1. Сгруппируем выборку и запишем статистические ряды абсолютных и относительных частот. Построим вариационный ряд – выборку в порядке возрастания:  Найдем размах выборки Число интервалов 𝑁, на которые следует разбить интервал значений признака, найдём по формуле Стерджесса:  объём выборки, то есть число единиц наблюдения. Для  получим:  Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Округление шага производится, как правило, в большую сторону. Таким образом, принимаем ℎ = 10. За начало первого интервала принимаем такое значение из интервала чтобы середина полученного интервала оказалась удобным для расчетов числом. В данном случае за нижнюю границу интервала возьмём 80. В результате получим следующие границы интервалов:  2) Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. Относительные частоты 𝑚∗ определим по формуле: 𝑚∗ = 𝑚 𝑛 Номер интервала Интервал Середина интервала Частота 𝑚 Относительная частота 𝑚∗ Накопление  3. Представим графически статистический ряд в виде гистограммы относительных частот. 4. Построим график накопленных относительных частот. 5. Составим эмпирическую функцию распределения. Эмпирическая функция распределения выглядит следующим образом 𝐹(𝑥) = { 0  6. Вычислим точечные оценки параметров законов распределения: 1) выборочное среднее;  2) выборочную смещённую 𝐷в (неисправленную) дисперсию и выборочную несмещённую 𝑆 2 (исправленную) дисперсию; 3) выборочное неисправленное 𝜎в среднее квадратическое отклонение и выборочные исправленное 𝑆 среднее квадратическое отклонение;  4) выборочную моду (значение, соответствующее наибольшей частоте); Для интервального ряда (с равными интервалами) мода определяется по следующей формуле:  нижнее значение модального интервала;  частота в модальном интервале; 𝑓𝑀𝑜−1 – частота в предыдущем интервале;  частота в следующем интервале за модальным; ℎ – размах интервала. Модальный интервал – это интервал с наибольшей частотой, т.е. в данном случае. Тогда 5) выборочную медиану. Медианой в статистике называют варианту, расположенную в середине вариационного ряда. Для интервального ряда медиану определяют по формуле:  нижняя граница интервала, в котором находится медиана; ℎ – размах интервала; накопленная частота в интервале, предшествующем медианному; 𝑓𝑀𝑒 – частота в медианном интервале. Медианный интервал – это тот, на который приходится середина ранжированного ряда, т.е. в данном случае  Доверительный интервал для математического ожидания a нормально распределенной случайной величины:  такое значение аргумента функции Лапласа, при котором. Для по таблице функции Лапласа находим 𝑡 из равенства:  Получаем  и искомый доверительный интервал имеет вид: