Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2)

СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) Теория вероятностей
СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) Решение задачи
СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2)
СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) Выполнен, номер заказа №16373
СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) Прошла проверку преподавателем МГУ
СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2) СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2)  245 руб. 

СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2)

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2)

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется:

 1) записать p(x), F(x) ; 2) найти P(  X  ) ; 3) найти P( X  a 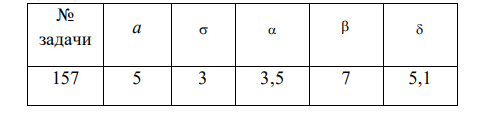 ) . СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2)

Решение

1) Плотность распределения вероятности нормально распределенной случайной величины имеет вид  При  получим  Функция распределения 𝐹(𝑥) имеет вид где Ф(𝑥) – функция Лапласа. 2) Для нормального закона распределения случайной величины вероятность попадания в заданный интервал равна:  3) Вероятность того, что модуль отклонения случайной величины Х от своего математического ожидания 𝑎 меньше любого положительного 𝑚, равна  где Ф(𝑥) – функция Лапласа. При заданных условиях:

СВ Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением . Требуется: 1) записать p(x), F(x) ; 2)