Движение твердого тела, имеющего неподвижную точку в теоретической механике

Движение твердого тела, имеющего неподвижную точку:

Движением твердого тела, имеющего неподвижную точку, или сферическим движением тела, называется такое его движение, когда одна из точек тела во все время его движения остается неподвижной.

Проведя из неподвижной точки ряд концентрических сфер возрастающих радиусов, мы можем рассматривать тело состоящим из отдельных тонких сферических оболочек (сфер), соединенных между собой и наложенных одна на другую. Положение твердого тела в любой момент вполне определится, если будет известно перемещение одной из оболочек (сферической фигуры) по неподвижной сфере. Подобно тому, как положение плоской фигуры на плоскости, по которой она движется, вполне определяется каким-либо отрезком АВ, принадлежащим этой плоскости, так и положение сферической фигуры, а следовательно, и всего тела вполне определяется положением дуги АВ большего круга сферы (рис. 202).

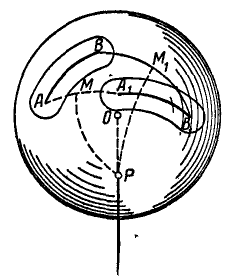
Рис. 202.

Не трудно показать, что твердое тело, имеющее неподвижную точку, может быть перемещено из данного положения в какое-либо другое простым вращением вокруг некоторой оси, проходящей через неподвижную точку.

В этом заключается теорема Эйлера, которая доказывается так же, как и теорема Эйлера для плоского движения (см. § 25).

Пусть в данный момент положение сферической фигуры определяется дугой большого круга АВ (рис. 202), а по истечении некоторого промежутка времени дугой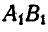

Осью вращения сферы является прямая, проходящая через центр сферы О и точку Р.

В самом деле, если мы повернем сферу вокруг оси ОР на , то точка А совпадет с и 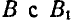, а дуга АВ с дугой .

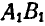Ясно, что перемещение дуги 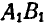в какое-либо другое положение может быть воспроизведено уже вокруг другой оси  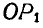и т. д.

Если мы будем рассматривать ряд элементарных перемещений дуги АВ большого круга, принадлежащей сферической фигуре, то каждое из этих перемещений, происходящее за время 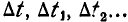, может быть воспроизведено вращением вокруг своей оси, проходящей через неподвижную точку О (рис. 202). При 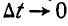каждое из бесконечно малых перемещений дуги будет происходить уже вокруг мгновенной оси; эти оси в пределе образуют в неподвижном пространстве некоторую коническую поверхность называемую неподвижным аксоидом (рис. 203).

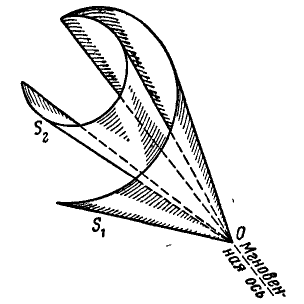
Рис. 203.

Отметив в теле все прямые, которые при движении его приходят последовательно в совпадение с образующими неподвижного аксоида, мы получим геометрическое место этих прямых, которое также является конической поверхностью и называется подвижным аксоидом .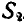

Отсюда следует, что подвижной аксоид, перемещаясь вместе с телом, имеет в каждый момент общую образующую (мгновенную ось) с неподвижным аксоидом (рис. 203) и катится без скольжения по неподвижному аксоиду.

Это положение читается так:

Всякое непрерывное движение твердого тела около неподвижной точки может быть воспроизведено качением без скольжения подвижного аксоида по неподвижному; при этом линия касания обоих аксоидов является мгновенной осью вращения тела.

Доказывается эта теорема аналогично теореме для плоского движения (см. § 25).

Перейдем теперь к нахождению мгновенной угловой скорости тела, имеющего неподвижную точку. Представим себе, что неподвижная точка О тела является началом двух систем координат, из которых одна Oxyz неподвижна относительно пространства, а другая    связана с телом и вместе с ним перемещается (рис. 204).

Рис. 204.

Назовем линию ОК пересечения плоскости хОу и узловой линией, а прямую OL, лежащую в плоскости и перпендикулярную к узловой линии,— поперечной осью. Легко видеть, что положение подвижной системы координат 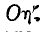, а следовательно, и тела, связанного с этой системой, вполне определяется заданием трех углов: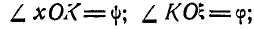  

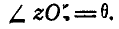
Эти углы называются эйлеровыми углами и носят названия: 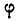 — угол собственного вращения,  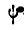 — угол прецессии и 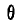— угол нутации. С течением времени эйлеровы углы изменяются, поэтому они являются функциями времени:

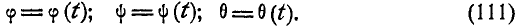
Эти уравнения, заданием которых определяется положение тела в любой момент, называются уравнениями вращения твердого тела, имеющего неподвижную точку.

Как уже было отмечено, движение твердого тела, имеющего неподвижную точку, таково, что в каждый момент оно совершает простое вращение вокруг мгновенной оси.

Обозначив угловую скорость вращения тела вокруг мгновенной оси через 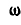, мы можем представить ее в виде вектора 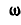, направленного по оси мгновенного вращения, которая на рисунке 204 не показана.

Вектор мгновенной угловой скорости 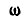, как и всякий вектор, можно разложить на три компонента по любым трем направлениям.

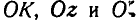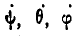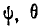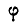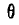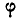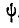В нашем случае это разложение вектора ш удобно произвести по направлению осей: (рис. 204), так как такое разложение соответствует заданным уравнениям (111) движения тела. В самом деле, чтобы определить компоненты угловой скорости , соответствующие эйлеровым углам, рассмотрим последовательно такие движения тела, при которых изменяется только один из этих углов или , в то время как два других — и 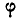,  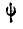 и , и 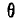— не изменяются.

Для нахождения проекций мгновенной угловой скорости 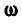тела на оси 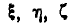, достаточно найти проекции на эти оси ее компонентов 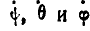, отложенных по осям 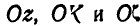. Составление этих проекций сведено в таблицу 8.

Таблица 8
    

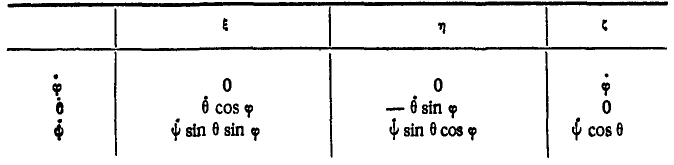
При нахождении проекций вектора 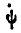на ос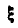и и 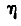 следует сначала вектор 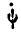спроектировать на поперечную ось, а затем уже полученную проекцию на поперечной оси еще раз спроецировать на ос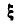и и .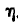

Обозначая проекции вектора 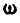на координатные оси 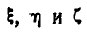через 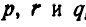, найдем:

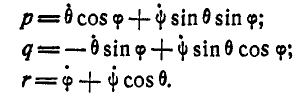
Эти равенства называются кинематическими уравнениями Эйлера и являются основными при аналитическом исследовании вращения тела вокруг неподвижной точки.

В отличие от тела, имеющего неподвижную ось вращения, направление мгновенной оси тела, имеющего неподвижную точку, непрерывно меняется. Так как в каждый момент вектор мгновенной угловой скорости направлен по мгновенной оси, то, следовательно, изменение вектора мгновенной угловой скорости происходит не только по величине, но и по направлению.

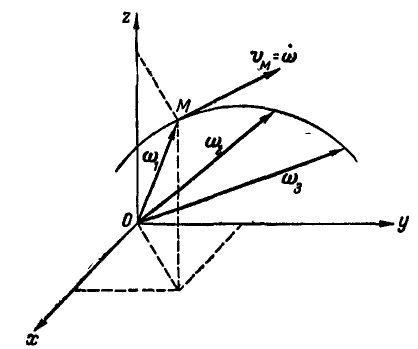
Рис. 205.  

 Подобно годографу линейной скорости точки, годографом угловых скоростей тела называется кривая (рис. 205), представляющая собой геометрическое место концов векторов угловых скоростей 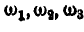, проведенных из неподвижной точки О.

Так как координаты точки М, вычерчивающей годограф, соответственно равны 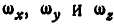, то ее скорость 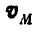геометрически равна угловому ускорению 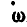, т.е.

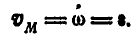
Перейдем к вопросу определения скоростей и ускорений точек тела.

Линейная скорость 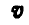любой точки тела может быть найдена по формуле (100); это следует из того, что в каждый момент движение тела таково, что оно совершает простое вращение вокруг мгновенной оси.

Проектируя векторное произведение 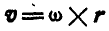 сначала на неподвижные х, у, z, а затем на подвижные, связанные с телом, координатные оси 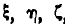, найдем по формулам (101) проекции линейной скорости на две указанные системы координатных осей:

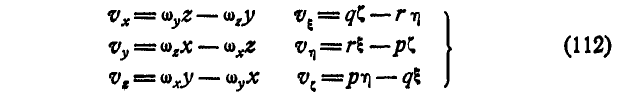
Эти равенства называются формулами Эйлера. Для точек, лежащих на мгновенной оси, скорость 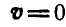, поэтому, полагая 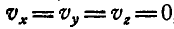, получим уравнение мгновенной оси в неподвижных координатах:

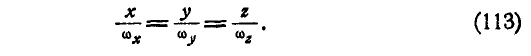
Аналогично, полагая 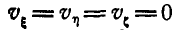, получим уравнение мгновенной оси в подвижных координатах:

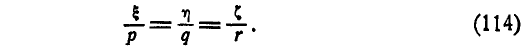
Исключая время t из уравнений (113), найдем уравнение неподвижного аксоида, а из уравнений (114) — уравнение подвижного аксоида.

Проекция ускорения на ось х любой точки тела:

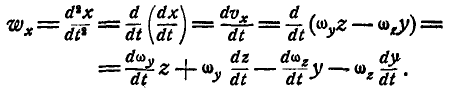
Подставляя вместо 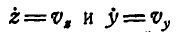их значения из первых равенств (112) и прибавляя к правой части 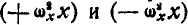, получим окончательное значение 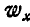, а также по аналоги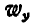и и 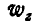по формулам:

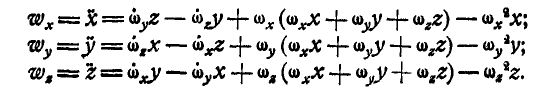
Ускорение любой точки тела можно найти иначе. По формуле (103) имеем:

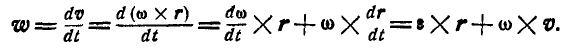
В противоположность вращению тела вокруг неподвижной оси, вектор углового ускорения 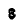 направлен по мгновенной оси вращения, так как вектор угловой скорости  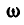непрерывно меняет свое направление в пространстве (рис. 206).

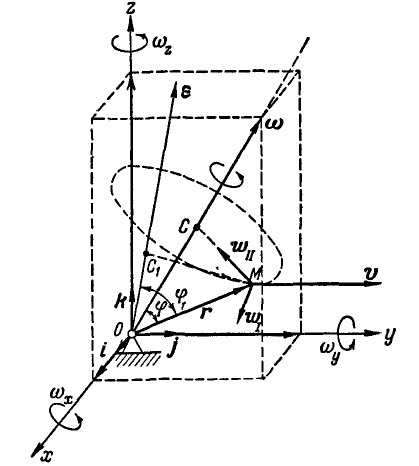
Рис. 206.

Введя обозначения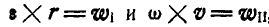 , имеем:

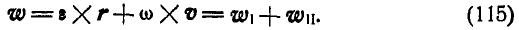
Итак, полное ускорение точек тела, имеющего неподвижную точку в каждый момент времени, есть геометрическая сумма двух ускорений:

1. ускорения 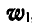, представляющего момент углового ускорения относительно данной точки,  равного по величине  и называемого вращательным ускорением;
2. ускорения , направленного no радиусу вращения по направлению к мгновенной оси, равного по величине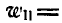 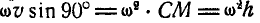и называемого осестремительным ускорением.

• Заказать решение задач по теоретической механике

Задача:

Конус, образующая которого 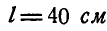, катится по плоскости без скольжения, имея вершину в неподвижной точке О (рис. 207). Определить векторы 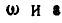, а также скорости и ускорения точек А и В основания конуса, если угол при вершиие равен 60°, а центр основания конуса С описывает окружность в течение 4 сек.

Решение. Мгновенная ось конуса в данный момент совпадает с образующей ОА, так как эта образующая проходит через неподвижную точку О и, соприкасаясь с неподвижной плоскостью, проходит через точки, скорости которых равны нулю.

Вектор угловой скорости мгновенного вращения 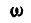 направлен по мгновенной оси.

При движении центра основания конуса С по окружности радиуса R скорость его 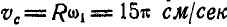, так как 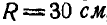, a .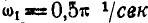

С другой стороны, известно, что конус совершает в данный момент простое вращение вокруг мгновенной оси ОА с угловой скоростью 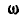, поэтому 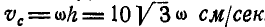. Следовательно, 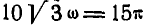откуда:

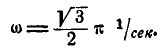
Рассматривая 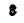как скорость конца вектора 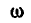и зная, что вектор 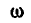вращается по условию с угловой скоростью 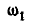вокруг вертикальной оси, найдем величину :

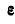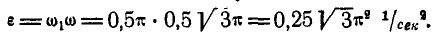
По направлению перпендикулярно . Линейные скорости точек А и В соответственно равны: 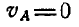и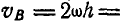

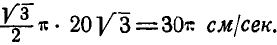
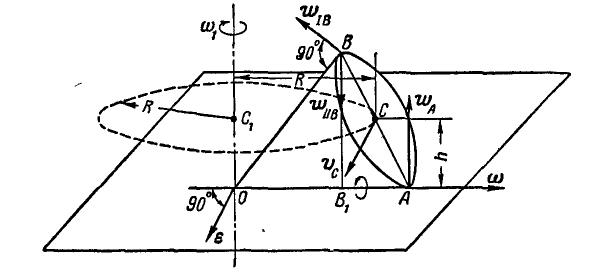
Рис. 207.

Так как точка А лежит на мгновенной оси, то осестремитель-ное ее ускорение 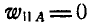, а вращательное ускорение:

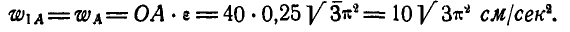
Направление показано на рисунке 207.

Применяя доказанную теорему для точки В, найдем ее осестремительное и вращательное ускорения по формулам:

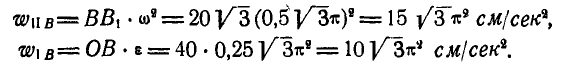
Направление вектора 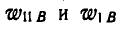 также показано на рисунке 207.

Полное ускорение 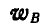точки В изобразиться диагональю паралелограмма, построенного на векторах .

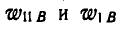Задача:

Угловая скорость тела 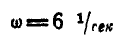. Направление мгновенной оси составляет в данный момент времени с осями координат углы 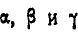; 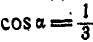,  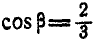и . Найти такую точку тела, находящуюся на плоскости 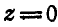, проекции скорости которой на координатные оси  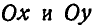равны: 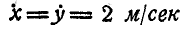. Найти также уравнение мгновенной оси.

Решение. Для определения 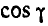воспользуемся зависимостью: 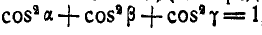, откуда:

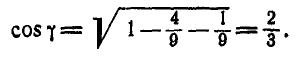
Так как по условию , то .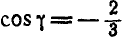

Найдем теперь проекции угловой скорости на координатные оси 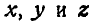по формулам:

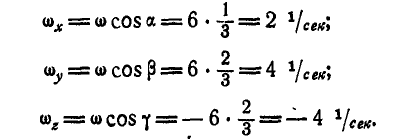
Применяя формулы Эйлера (112) для неподвижных осей х, у и z, имеем:

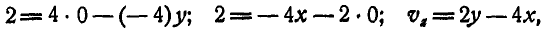
откуда

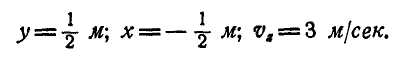
Для нахождения уравнения мгновенной оси возьмем любую точку на мгновенной оси с координатами 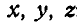; так как всякая точка мгновенной оси имеет скорость, равную нулю, то для этой точки формулы Эйлера (112) примут вид:

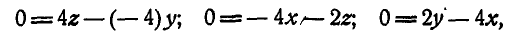
или

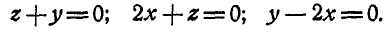
Мгновенную ось можно выразить любыми двумя из этих уравнений, так как каждое третье уравнение может быть получено из двух остальных.