
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или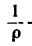
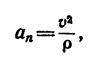
Отсюда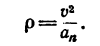
Скорость 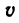 точки определяется по формуле
точки определяется по формуле
Следовательно,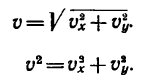
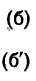
Числовое значение нормального ускорения а„ входит в выражение полного ускорения точки
откуда

где квадрат полного ускорения

и касательное ускорение
Таким образом, если закон движения точки задан уравнениями 
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:

2. Подставив в (б’) выражения 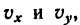 найти
найти 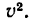
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б'), найти касательное ускорение 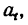 а затем а?.
а затем а?.
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
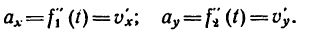
5. Подставив в (г) выражения 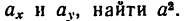
6. Подставить в (в) значения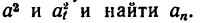
7. Подставив в (а) найденные значения 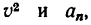 получить радиус кривизны р.
получить радиус кривизны р.
Задача:
Движение точки задано уравнениями 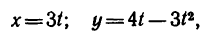
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
Решение.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
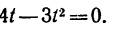
Отсюда [решая уравнение относительно 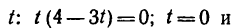
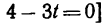 находим, что траектория пересекает ось Ох в моменты времени
находим, что траектория пересекает ось Ох в моменты времени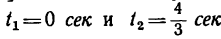
2. Находим выражения проекций скорости:
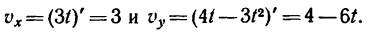
Как видно, проекция скорости на ось Ох - постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
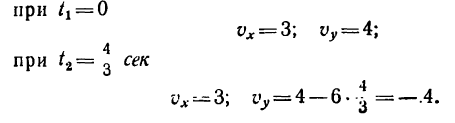
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
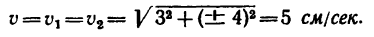
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
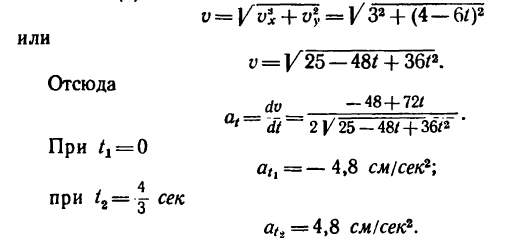
6. Находим проекции полного ускорения точки:
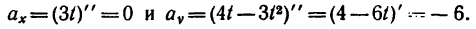
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
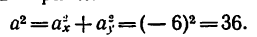
7. Определяем нормальное ускорение точки. Как при 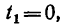
так и при 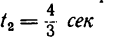
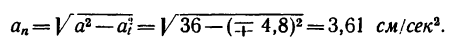
8. Зная, что в моменты пересечения траекторией оси 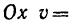 5 см:сек и
5 см:сек и 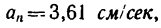 находим радиусы кривизны траектории в этих точках:
находим радиусы кривизны траектории в этих точках:
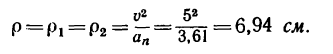
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 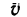 и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы
и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы 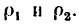
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки