
Переходные процессы в линейных цепях
Содержание:
Переходные процессы в линейных цепях и их расчет классическим методом:
Процессы в электрических цепях, рассматривавшиеся до сих пор, были установившимися процессами. В этой главе изучаются переходные процессы, которые происходят при всех изменениях режима электрической цепи — включении, выключении, коротком замыкании и т. п. Эти процессы не могут протекать мгновенно, так как невозможны мгновенные изменения энергии, запасенной в электромагнитном поле цепи.
В цепях с сосредоточенными параметрами энергия запасается в емкостях в виде энергии 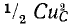
Для расчета переходных процессов в цепях составляется система уравнений по законам Ома и Кирхгофа для мгновенных значений напряжений и токов. Эта система приводится к одному уравнению для одного из напряжений или токов, которое в общем случае линейных цепей будет линейным обыкновенным дифференциальным уравнением. Порядок этого уравнения можно определить из упрощенной схемы цепи, объединяя индуктивности и, соответственно, емкости, соединения между которыми являются последовательными и параллельными или приводятся к ним. Тогда искомый порядок равен числу независимых начальных условий для токов индуктивностей и напряжений на емкостях упрощенной схемы. Например, если три индуктивности соединены в звезду, объединить их нельзя, но можно задать только два независимых начальных условия в виде токов двух индуктивностей, так как ток третьей определяется через первые два. Для цепи с последовательным соединением r, L и С (см. рис. 7.1, a) уравнение, связывающее напряжение и цепи с током i, будет второго порядка, так как начальные значения i и uс могут быть заданы независимо друг от друга:
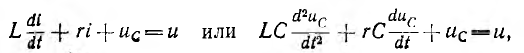
так как 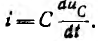
Как известно из математики, решение линейных дифференциальных уравнений с постоянными коэффициентами представляет собой сумму двух решений, например,
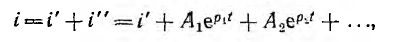
где i' — частное решение неоднородного уравнения, a i" — общее решение однородного уравнения, выраженное через постоянные интегрирования 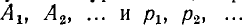 — корни характеристического уравнения для случая, когда все корни различны.
— корни характеристического уравнения для случая, когда все корни различны.
Частное решение i" неоднородного уравнения определяется видом функции, стоящей в правой части уравнения, и поэтому называется принужденным. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников энергии принужденное решение совпадает с установившимися значениями искомых величин и определяется известными из предыдущего методами расчета цепей.
Общее решение i" однородного уравнения описывает процесс, происходящий без воздействия внешних источников за счет изменения запаса энергии, накопленной в цепи до начала переходного процесса; оно имеет одинаковый вид для любого переходного процесса в данной цепи. Это решение называют свободной составляющей переходного процесса. Так как запасенная в цепи энергия при отсутствии внешних источников будет постепенно расходоваться, свободная составляющая с течением времени уменьшится до нуля. Математически это соответствует отрицательным вещественным корням или отрицательным вещественным частям комплексных корней рк характеристического уравнения, что вызывает убывание во времени функций вида 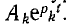
Сумма принужденной и свободной составляющих 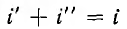 представляет собой искомую величину, в данном примере ток; она называется переходной.
представляет собой искомую величину, в данном примере ток; она называется переходной.
Исходя из выражения для переходной величины, определяют постоянные интегрирования 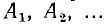 из начальных условий — значений напряжений uс (0) на емкостях и токов iL (0) в индуктивностях, которые имели место до начала переходного процесса и, в соответствии со сказанным о невозможности скачков, будут теми же и в начальный момент переходного процесса.
из начальных условий — значений напряжений uс (0) на емкостях и токов iL (0) в индуктивностях, которые имели место до начала переходного процесса и, в соответствии со сказанным о невозможности скачков, будут теми же и в начальный момент переходного процесса.
Переходный ток превращается в принужденный, когда затухнет свободный ток. Математически строго это наступит при t - оо, практически время переходных процессов в большинстве электрических цепей исчисляется долями секунды.
В переходном процессе при коротком замыкании цепи свободная составляющая равна переходной величине, так как тогда правая часть уравнения, например приложенное к цепи напряжение, а следовательно, и принужденная составляющая переходной величины будут равны нулю. Поэтому при изучении переходных процессов в различных цепях целесообразно сначала рассмотреть их короткое замыканне, а определенный при этом общий вид переходной величины использовать, как свободную составляющую для других переходных процессов.
Таким образом, методика расчета переходных процессов, называемая классической, состоит в составлении дифференциальных уравнений для цепи, их решении и определении постоянных интегрирования из начальных условий.
Переходные процессы в цепи с последовательным соединением сопротивления и индуктивности
Короткое замыкание цепи:
При коротком замыкании цепи с последовательным соединением r и L (рис. 15.1, а) уравнение переходного тока i, равного в этом случае свободному току i", имеет вид:
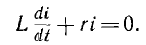
Характеристическое уравнение Lp + r = О
имеет корень 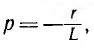
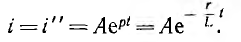
Если до момента короткого замыкания по цепи шел постоянный ток 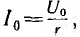 , где U0 — постоянное напряжение цепи (рис. 15.1, б),
, где U0 — постоянное напряжение цепи (рис. 15.1, б),
это значение тока сохранится и для первого мгновения после замыкания цепи, откуда определяется постоянная интегрирования:
следовательно, 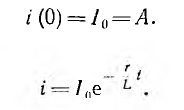
Это выражение изображается затухающей кривой — экспонентой, ордината которой при t = 0 равна I0. Уменьшение тока i происходит тем быстрее, чем больше коэффициент затухания 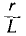 или чем меньше обратная величина
или чем меньше обратная величина 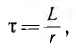 имеющая размерность времени и называемая постоянной времени. По истечении времени
имеющая размерность времени и называемая постоянной времени. По истечении времени 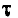 с любого момента t переходный ток
с любого момента t переходный ток
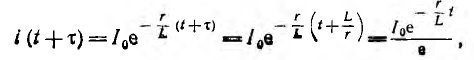
т. е. в е = 2,718 ... раз меньше своего первоначального значения. Так как
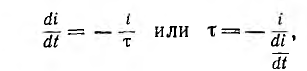
постоянная времени равна длине подкасательной в любой точке кривой i (см. рис. 15.1, б). За время, равное 4,6 т, переходный ток затухает до значения 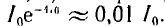 Так как переходный ток при коротком замыкании равен свободному току и для других переходных процессов в этой цепи, для большинства инженерных задач можно считать, что переходный процесс за время
Так как переходный ток при коротком замыкании равен свободному току и для других переходных процессов в этой цепи, для большинства инженерных задач можно считать, что переходный процесс за время 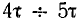 практически заканчивается. Постоянная времени цепей обычно невелика; для катушек без ферромагнитных сердечников она составляет десятые доли секунды.
практически заканчивается. Постоянная времени цепей обычно невелика; для катушек без ферромагнитных сердечников она составляет десятые доли секунды.
В короткозамкнутой цепи появляется э. д. с. самоиндукции
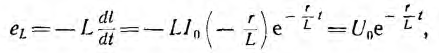
поддерживающая ток. Эта э. д. с. возникает при коротком замыкании цепи скачкообразно, принимая значение U0 при t= 0(см. рис. 15.1 б).
Энергия, расходуемая на нагрев сопротивления г цепи за время переходного процесса
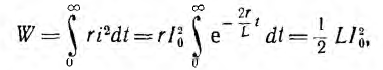
равна энергии, запасенной в индуктивности до замыкания цепи.
Процессы будут протекать аналогично и при коротком замыкании цепи переменного тока, но тогда I0 будет мгновенным значением тока цепи в момент замыкания.
Замыкание цепи на добавочное сопротивление
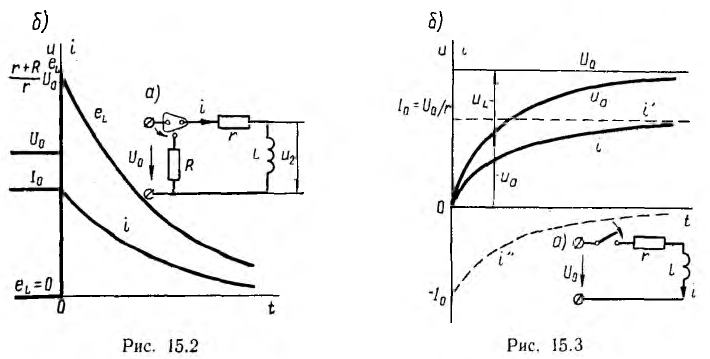
Предполагается, что цепь r, L, отключаясь от источника напряжения U0, замыкается на добавочное сопротивление R без предварительного размыкания цепи, что можно осуществить с помощью переключателя, схематически показанного на рис. 15.2, а. Для тока цепи после переключения может быть использовано полученное в п. 1 выражение, но сопротивление цепи теперь равно r+R:
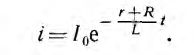
Из-за уменьшения постоянной времени ток будет затухать быстрее (рис. 15.2, б). Э. д. с. самоиндукции
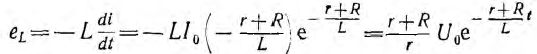
е,
поддерживает в цепи ток 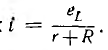 Значение э. д. с. в первый момент после переключения
Значение э. д. с. в первый момент после переключения
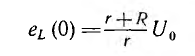
больше напряжения U0 во столько раз, во сколько увеличилось сопротивление цепи. Это явление называется перенапряжением.
Казалось бы, что процесс размыкания цепи можно рассматривать как замыкание цепи на добавочное сопротивление R = 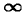 ; но при этом перенапряжение, а следовательно, и напряжение на выключателе должно в первый момент равняться бесконечности, чего быть не может. В действительности под воздействием возрастающего напряжения произойдет пробой промежутка между контактами выключателя, и в цепь окажется включенным увеличивающееся по мере разведения контактов сопротивление электрической дуги. Цепь и ее уравнение становятся нелинейными, и расчет не может быть выполнен элементарным путем. Эта задача является основной в теории выключающей аппаратуры.
; но при этом перенапряжение, а следовательно, и напряжение на выключателе должно в первый момент равняться бесконечности, чего быть не может. В действительности под воздействием возрастающего напряжения произойдет пробой промежутка между контактами выключателя, и в цепь окажется включенным увеличивающееся по мере разведения контактов сопротивление электрической дуги. Цепь и ее уравнение становятся нелинейными, и расчет не может быть выполнен элементарным путем. Эта задача является основной в теории выключающей аппаратуры.
Включение цепи на постоянное напряжение
При включении цепи r, L на постоянное напряжение U0 (рис. 15.3, а) принужденный ток 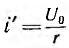 переходный ток
переходный ток
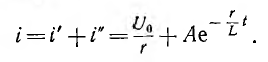
Ток до переходного процесса, а следовательно, и в первый момент после включения равен нулю:
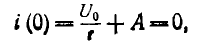
отсюда
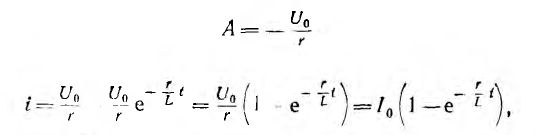
т. е. переходный ток постепенно нарастает до своего окончательного значения I0 и тем медленней, чем больше постоянная времени 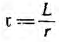 (рис. 15.3, б); здесь показаны также принужденная и свободная составляющие переходного тока.
(рис. 15.3, б); здесь показаны также принужденная и свободная составляющие переходного тока.
Напряжения на участках цепи
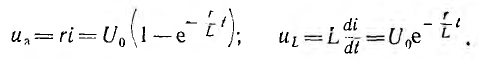
Следовательно, в первый момент напряжение цепи целиком сосредоточивается на индуктивности и затем постепенно переходит на сопротивление.
Изменение сопротивления цепи
Пусть в цепи r + R, L (рис. 15.4, а) рубильник то замыкается, шунтируя резистор R, то размыкается, вновь включая этот резистор, причем промежутки между переключениями больше времени практического установления процесса.
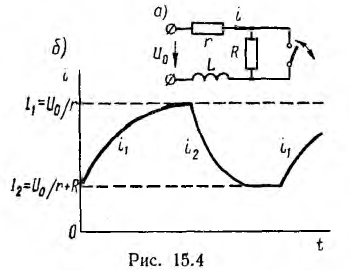
Тогда принужденный ток меняется от значения
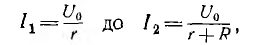
и переходный ток после замыкания рубильника
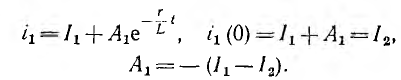
Окончательно
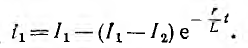
После размыкания переходный ток
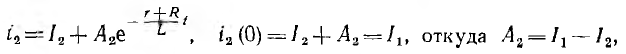
и окончательно
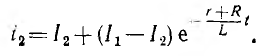
График изменения тока в цепи изображен на рис. 15.4, в-, процесс осле размыкания рубильника устанавливается быстрей, так как постоянная времени цепи меньше, чем после замыкания.
Включение цепи на синусоидальное напряжение
Пусть цепь r, L включается на синусоидальное напряжение 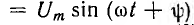 (рис. 15.5, а). Тогда значение напряжения в момент включения
(рис. 15.5, а). Тогда значение напряжения в момент включения 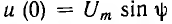 определяется величиной начальной фазы ψ, которая в этом случае называется также фазой включения.
определяется величиной начальной фазы ψ, которая в этом случае называется также фазой включения.
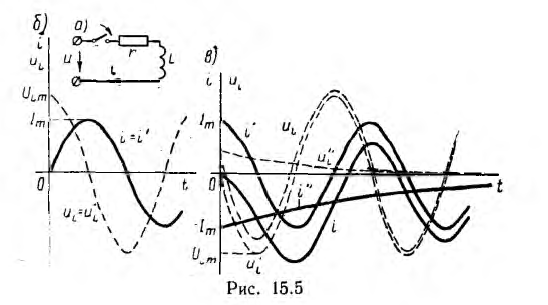
Принужденный ток
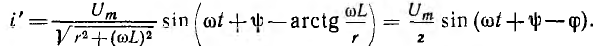
Переходный ток
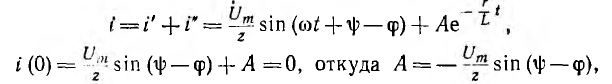
и окончательно
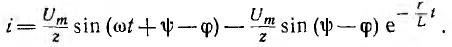
Переходное напряжение на сопротивлении пропорционально току ua = ri, а на индуктивности
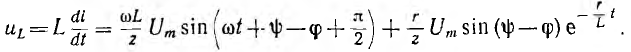
При включении в момент, когда принужденный ток равен нулю, например при 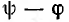 = 0,
= 0,
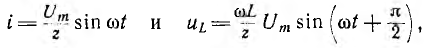
т. е. свободного тока и свободных напряжений на участках цепи нет, и сразу после включения наступает установившийся процесс (рис. 15.5, б).
В общем случае на синусоидальные установившиеся напряжения на участках цепи и ток налагаются свободные составляющие, значения которых уменьшаются по показательному закону. В результате ток и напряжения uа и uL в течение некоторых промежутков времени могут превосходить их максимальные значения 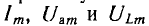 при установившемся режиме, т. е. могут возникнуть большой ток, называемый сверхтоком, и перенапряжения. Их величина зависит от фазы включения ψ и от постоянной времени
при установившемся режиме, т. е. могут возникнуть большой ток, называемый сверхтоком, и перенапряжения. Их величина зависит от фазы включения ψ и от постоянной времени 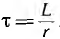 , определяющих соответственно, начальные значения свободных составляющих и скорость их уменьшения. Так, при включении в момент, когда принужденный ток получает максимальное значение
, определяющих соответственно, начальные значения свободных составляющих и скорость их уменьшения. Так, при включении в момент, когда принужденный ток получает максимальное значение 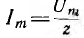 например при
например при 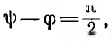
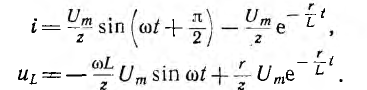
При большой постоянной времени получается большой сверхток (рис. 15.5, в), однако он не может превзойти двойную амплитуду 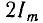 установившегося тока. Аналогично поведение
установившегося тока. Аналогично поведение 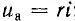 , перенапряжение же для uL меньше, так как в этом случае r и uL малы.
, перенапряжение же для uL меньше, так как в этом случае r и uL малы.
Переходные процессы в цепи с последовательным соединением сопротивления и емкости
Короткое замыкание цепи:
При коротком замыкании цепи с последовательным соединением r и С (рис. 15.6, а)
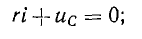
так как 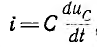 , уравнение для переходного емкостного напряжения uс. равного в этом случае его свободному значению u''с, будет
, уравнение для переходного емкостного напряжения uс. равного в этом случае его свободному значению u''с, будет
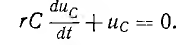
Характеристическое уравнение
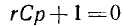
корень 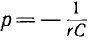 , тогда
, тогда
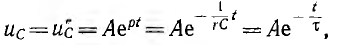
где 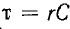 — постоянная времени этой цепи.
— постоянная времени этой цепи.
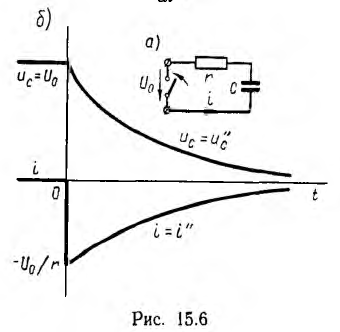
Если начальное напряжение на емкости было равно U0 оно сохранится и для первого мгновения после замыкания, откуда определится постоянна интегрирования:
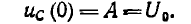
Следовательно, напряжение на емкости убывает по экспоненте (рис. 15.6, б):
Ток 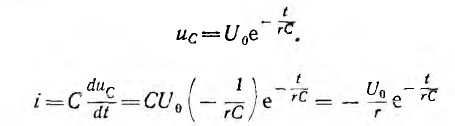
возникает при коротком замыкании цепи скачкообразно, принимая значение 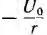 затем убывает по тому же экспоненциальному закону.
затем убывает по тому же экспоненциальному закону.
Так как это ток разряда, знак его отрицательный. Энергия, расходуемая на нагрев сопротивления r за время переходного процесса,
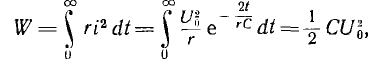
т. е. равна энергии, запасенной в емкости до замыкания цепи.
Включение цепи на постоянное напряжение
При включении цепи r, С на постоянное напряжение U0 (рис. 15.7, а) емкость будет заряжаться до принужденного напряжения u'с = U0. Тогда переходное напряжение
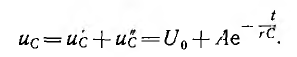
Напряжение на емкости до переходного процесса, а следовательно, и в первый момент после включения равно нулю:
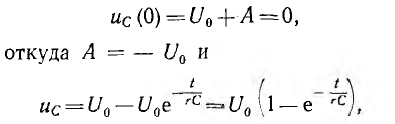
т. е. напряжение на емкости постепенно нарастает до своего окончательного значения и тем медленней, чем больше постоянная времени 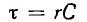 (рис. 15.7, б).
(рис. 15.7, б).
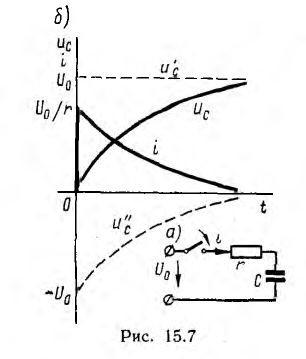
Ток зарядки
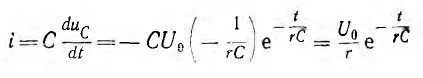
три включении цепи возникает скачком и изменяется по тому же некартельному закону, что и ток разряда, но имеет положительный знак. Следовательно, энергия, расходуемая на нагрев сопротивления за время переходного процесса, независимо от величины r будет такой же как и в случае разряда, т. е. 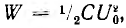 , и равна энергии, которая запасается в емкости при ее зарядке.
, и равна энергии, которая запасается в емкости при ее зарядке.
Интересно отметить, что при зарядке конденсатора постоянны током I0, например от источника тока с пренебрежимо малой внутренней проводимостью, время зарядки до заданного напряжения U было бы 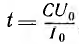 т. е. конечным, а потери в сопротивлении
т. е. конечным, а потери в сопротивлении 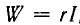 при малом r будут малы.
при малом r будут малы.
Включение цепи на синусоидальное напряжение
При включении цепи r, С на синусоидальное напряжение 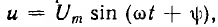 где ψ — фаза включения (рис. 15.8, а), принужденное напряжение на емкости
где ψ — фаза включения (рис. 15.8, а), принужденное напряжение на емкости
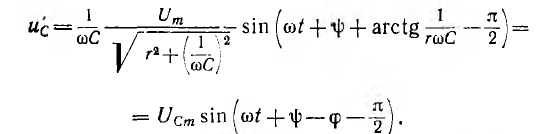
Переходное напряжение
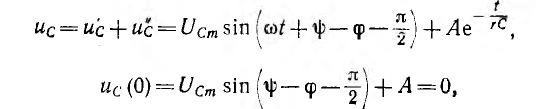
откуда постоянная интегрирования
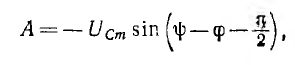
окончательно
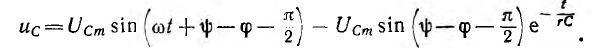
переходный ток цепи
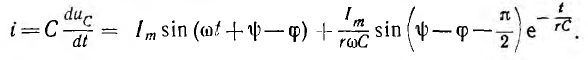
При включении в тот момент, когда принужденное напряжение на емкости равно нулю, например при 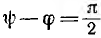 .
.
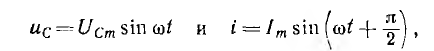
т. е. сразу после включения наступает установившийся процесс.
В общем случае на синусоидальные установившиеся напряжение на емкости и ток цепи налагаются свободные составляющие, значения которых уменьшаются по показательному закону. В результате ток i и напряжения 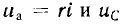 в течение некоторых промежутков времени могут превосходить максимальные значения
в течение некоторых промежутков времени могут превосходить максимальные значения 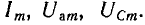 Величины сверхтока и перенапряжений зависят от фазы включения ψ и от постоянной времени rС, определяющих, соответственно, начальные значения свободных составляющих и скорость их уменьшения.
Величины сверхтока и перенапряжений зависят от фазы включения ψ и от постоянной времени rС, определяющих, соответственно, начальные значения свободных составляющих и скорость их уменьшения.
При включении в тот момент, когда принужденное напряжение на емкости получает максимальное значение Ucm, а принужденный ток равен нулю, например при  = О,
= О,
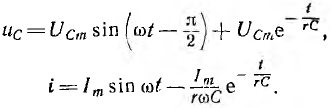
В этом случае при большой постоянной времени rС получается большое перенапряжение на емкости, равное в пределе двойной амплитуде 2Ucm установившегося напряжения на емкости, но малый сверхток (рис. 15.8, б). При малой постоянной времени может получиться сверхток 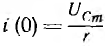 , во много раз превосходящий амплитуду Im тока установившегося режима, но тогда перенапряжения на емкости практически не будет (рис. 15.8, в).
, во много раз превосходящий амплитуду Im тока установившегося режима, но тогда перенапряжения на емкости практически не будет (рис. 15.8, в).
Переходные процессы в цепи с последовательным соединением сопротивления, индуктивности и емкости
Короткое замыкание цепи:
Как было показано, решение задачи короткого замыкания до определения постоянных интегрирования дает выражение для свободной составляющей тока или напряжения в цепи.
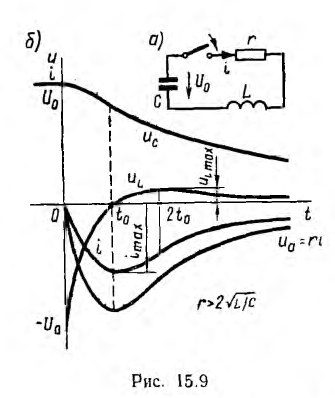
Пусть емкость, заряженная до напряжения U0 замыкается на цепи последовательным соединением сопротивления и индуктивности (рис. 15.9, а). Тогда уравнение по второму закону Кирхгофа будет одно родным:
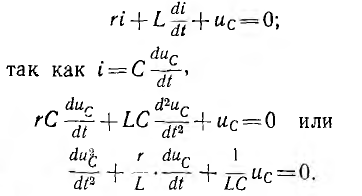
Характеристическое уравнение
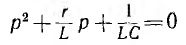
имеет два корня:
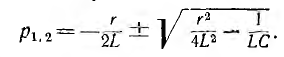
Если 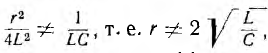 корни будут различными:
корни будут различными: 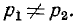 В этом случае решение дифференциального уравнения
В этом случае решение дифференциального уравнения
а ток цепи 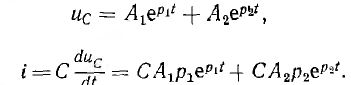
В момент t = 0 напряжение на емкости и ток индуктивности, равный току всей цепи, будут такими же, как и до замыкания:
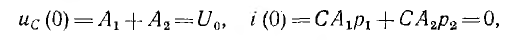
откуда постоянные интегрирования
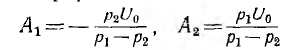
и, следовательно, ток и напряжения на участках будут:
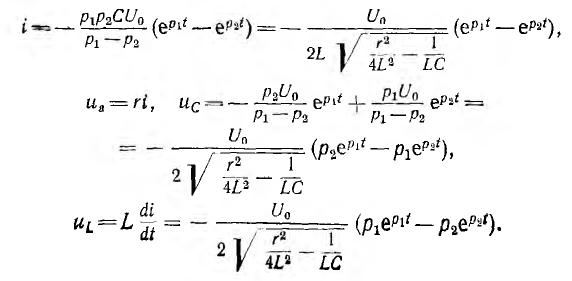
Характер переходного процесса зависит от соотношения между параметрами r, L и С цепи.
1. Если 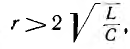 корни р1 и р2 будут вещественными, причем
корни р1 и р2 будут вещественными, причем 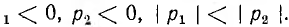 Этo значит, что все вычисленные выше величины состоят из алгебраической суммы двух экспонент, имеющих разные знаки, причем первая экспонента затухает медленней, чем вторая. В результате (рис. 15.9, б) напряжение конденсатора, начиная с U0, непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положительная и больше второй отрицательной. Ток i цепи и напряжение uа = ri на сопротивлении, начинаясь о нуля, всегда отрицательны, что соответствует току разряда. Напряжение uL на индуктивности возникает скачком, принимая значение —U0 проходит через нуль в момент t0 при равенстве значений своих экспонент, т. е. при
Этo значит, что все вычисленные выше величины состоят из алгебраической суммы двух экспонент, имеющих разные знаки, причем первая экспонента затухает медленней, чем вторая. В результате (рис. 15.9, б) напряжение конденсатора, начиная с U0, непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положительная и больше второй отрицательной. Ток i цепи и напряжение uа = ri на сопротивлении, начинаясь о нуля, всегда отрицательны, что соответствует току разряда. Напряжение uL на индуктивности возникает скачком, принимая значение —U0 проходит через нуль в момент t0 при равенстве значений своих экспонент, т. е. при 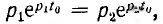 откуда
откуда
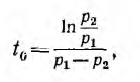
и затем становится положительным. Так как uL пропорционально производной 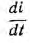 в момент t = t0 абсолютное значение тока проходит через максимум. Приравняв производную
в момент t = t0 абсолютное значение тока проходит через максимум. Приравняв производную 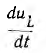 нулю, можно видеть, что uL имеет максимум при t = 2t0 (см. рис. 15.9,6). Рассмотренный вид разряда называется апериодическим.
нулю, можно видеть, что uL имеет максимум при t = 2t0 (см. рис. 15.9,6). Рассмотренный вид разряда называется апериодическим.
Энергетическая сторона апериодического процесса заключается в следующем.
Так как напряжение uс непрерывно уменьшается, емкость отдает энергию. Индуктивность с ростом тока накапливает энергию, но, начиная с t = t0, ток убывает и индуктивность постепенно отдает энергию. В течение всего процесса сопротивление рассеивает потребляемую им энергию.
2. Пусть 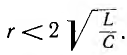 . Введя обозначения
. Введя обозначения
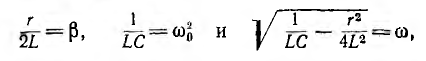
можно переписать выражение для корней характеристического уравнения следующим образом:
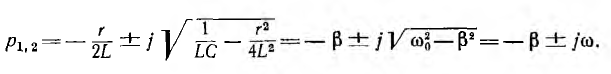
Так как ω — число вещественное, корни р1 и р2 будут комплексными.
После подстановки значений р1 и р2 и очевидных преобразований выражения для тока и напряжений на участках получат вид:
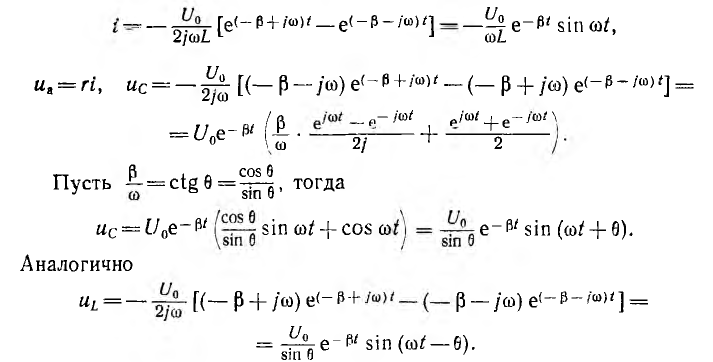
Ток и напряжения цепи, в которой r= 0 и, следовательно, β = 0, 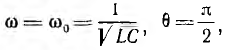 будут:
будут:
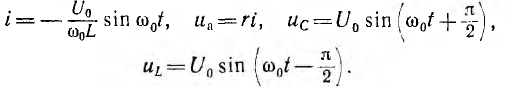
Следовательно, если бы в цепи не происходило рассеяние энергии, ток и напряжения на участках были бы синусоидальными функциями времени, т. е. имели бы место так называемые собственные незатухающие колебания, угловая частота которых равна резонансной частоте этой цепи 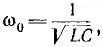 а период определяется по формуле Томсона:
а период определяется по формуле Томсона:
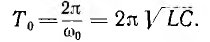
Для незатухающих колебаний на рис. 15.10 изображены векторная диаграмма и график мгновенных значений тока и напряжений на индуктивности и емкости, которые аналогичны имеющим место при резонансе в цепи с последовательным соединением r, L и С (см. рис. 7.4). Следовательно, и здесь происходит полный обмен энергиями между С и L.
Если в цепи есть сопротивление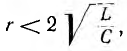 , разряд, как видно из приведенных выражений для тока и напряжений, также носит колебательный характер, но амплитуды тока и напряжений постепенно уменьшаются, так как
, разряд, как видно из приведенных выражений для тока и напряжений, также носит колебательный характер, но амплитуды тока и напряжений постепенно уменьшаются, так как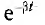 с ростом t стремится к нулю.
с ростом t стремится к нулю.
Угловая частота этих собственных затухающих колебаний
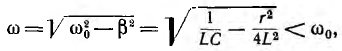
Период собственных затухающих колебаний 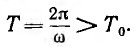
Отношение мгновенного значения какой-либо величины, например тока, к значению этой величины через период Т:
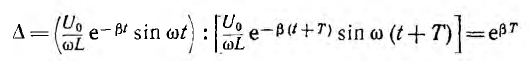
называется декрементом колебания.
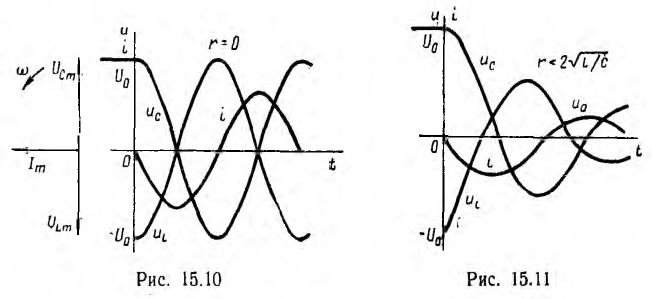
На рис. 15.11 изображен график мгновенных значений тока и напряжений для затухающих колебаний. Энергетический процесс заключается, в основном, в обмене энергиями между емкостью и индуктивностью с непрерывным рассеянием энергии сопротивлением. Переходный процесс закончится, когда энергия 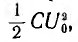 первоначально запасенная в емкости, будет целиком рассеяна.
первоначально запасенная в емкости, будет целиком рассеяна.
3. Если 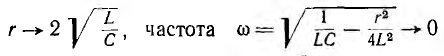 и стоящая
и стоящая
_ , sin в выражении тока в п. 2 дробь дает для этого критического случая Характер разряда будет апериодическим. При включении цепи r, L, С на постоянное напряжение (рис. 15.12, а) конденсатор будет заряжаться, и его установившееся напряжение uс = U0. Тогда Постоянные интегрирования определяются из начальных условий: Выражение для ис (0) отличается от выражения для uс (0) при коротком замыкании (п. 1) только знаком перед U0, выражения для i (0) График мгновенных значений для апериодического случая показан на рис. 15.12, б, для периодического — на рис. 15.12, е. При включении той же цепи на синусоидальное напряжение частоты ω1 ход решения остается тем же; переходные ток и напряжения на участках будут представлять собой сумму принужденных синусоидальных и свободных затухающих составляющих, носящих характер апериодический или колебательный с собственной частотой ω, в общем случае не равной частоте ω1. Переходный процесс в отличие от предыдущего случая будет зависеть также от момента включения. Общий случай сложных цепей: Как было указано, в общем случае разветвленной цепи )счет переходных процессов заключается в составлении системы зависимых уравнений по законам Кирхгофа для мгновенных значение напряжений и токов ветвей. Затем методом подстановки из одних равнений в другие исключаются отдельные неизвестные с тем, чтобы окончательное уравнение было дифференциальным уравнением с одним низвестным. Его целесообразно получить или для тока какой-либо идуктивности, или для напряжения на емкости. Это облегчит определение постоянных интегрирования из начальных условий и тогда спряжение на индуктивности и ток в емкости определяются путем дифференцирования, а не интегрирования, связанного с появлением новых постоянных. Известно, что в общем случае дифференциальные уравнения с одним неизвестным, полученные для любого неизвестного системы, будут иметь одно и то же характеристическое уравнение. Для электрических цепей это ясно и из того, что уравнения по Кирхгофу должны соблюдаться для любого момента времени, что возможно, когда свободные составляющие имеют одинаковые показатели, т. е. одинаковую зависимость от времени, и отличаются только постоянными коэффициентами. В качестве простого примера сделан расчет переходного процесса при включении цепи рис. 15.13 на постоянное напряжение U0. Основным неизвестным выбирается напряжение uс на емкости. Уравнения (одно по первому и два по второму законам Кирхгофа) имеют вид: Ток i2 определяется из (15.2) и результат подставляется в выражение для i1 полученное из (15.1): Затем определяется после чего выражения (15.5) и (15.6) подставляются в (15.3): Окончательно Получилось уравнение второго порядка, что и следовало ожидать так как в цепь включены одна индуктивность и одна емкость. Принужденное напряжение имеет различные корни, переходное напряжение Постоянные интегрирования определяются из начальных условий: После определения ис находят i, затем i2 из (15.4) В качестве простого примера рассматривается включение трансформатора без сердечника на постоянное напряжение U где r2 и L2 — суммарные сопротивление и индуктивность вторичной обмотки трансформатора и нагрузки. Для получения дифференциального уравнения с одним неизвестным i1 необходимо продифференцировать оба уравнения по t и умножить первое полученное уравнение на L2, а второе на М. Тогда вычитание второго из первого дает: после подстановки сюда из выражения (15.7) Окончательно Таким образом, получилось уравнение второго порядка. Хотя эквивалентная схема воздушного трансформатора содержит три необъединяемых индуктивности L1, L2 и М (см. рис. 11.9), но так как Оки в них связаны первым законом Кирхгофа, можно задать только ва независимых начальных условия, что и определяет порядок равнения. Дальнейший ход решения ясен, поэтому можно ограничиться общими соображениями. Так как подрадикальная величина в выражении корней характеристического уравнения то последнее имеет отрицательные вещественные корни, т. е. процесс протекает апериодически. Это ясно также из того, что цепь носит индуктивный характер и не имеет емкостей, наличие которых необходимо для обмена энергиями, т. е. для колебательного процесса. Начальные условия для токов из-за индуктивного характера цепи будут: i1(0) = 0 и i2 (0) = 0. Они позволят определить постоянные интегрирования. Принужденные токи Классический метод расчета переходных процессов привычен, так как он является общепринятым в других областях науки и техники, и нагляден, потому что при преобразованиях видна соответствующая физическая картина. Хотя постоянные интегрирования можно находить на основании заданных значений функций не только в начальный, но и в любые другие моменты времени, необходимость определения постоянных интегрирования усложняет использование классического метода. Оно особенно затруднительно для уравнений высоких порядков. Кроме того, как видно из приведенных примеров расчета переходных процессов в разветвленных цепях, при переходе от цепей, описываемых уравнением первого порядка, к системам второго порядка увеличиваются затруднения, связанные с преобразованием системы в уравнение с одним неизвестным. При дальнейшем повышении порядка отыскание нужных замен, связанное с промежуточным дифференцированием, еще более затрудняется. Так как решение дифференциального уравнения приводит к решению алгебраического характеристического уравнения, естественно стремление сразу представить систему исходных уравнений цег в алгебраической форме, что и осуществляется в спектральном и операторном методах (см. гл. XVII). Все предыдущие исследования электрических цепей касались установившихся режимов их работы, когда токи и напряжения были либо постоянны, либо менялись по некоторому периодическому закону. Кроме названных режимов, характеризующих устойчивое стационарное состояние цепи, существуют режимы, которые можно обобщенно охарактеризовать понятием переходные режимы или переходные процессы. Они возникают в результате включений и отключений цепей и отдельных участков или аварийных режимов, например, коротких замыканий, обрывов цепей, а также скачкообразных изменений параметров. Все эти изменения носят название коммутации. Во всех расчетах переходных процессов будем считать, что коммутация происходит мгновенно, т.е. без искрообразования. После коммутации в цепи возникает переходный процесс, который теоретически длится бесконечно долго. Однако фактическое время переходного процесса в подавляющем большинстве случаев чрезвычайно мало. Тем не менее, на отдельных участках цепи могут возникать большие перенапряжения или скачки тока, которые способны не только нарушить режим работы цепи, но и привести к порче оборудования. С физической точки зрения переходные процессы в цепях обусловлены наличием емкостей и индуктивностей, способных аккумулировать энергию электрического и магнитного полей. Если бы цепь не содержала указанных элементов и состояла бы только из активных сопротивлений, то переход её из одного стационарного состояния в другое происходил бы мгновенно. В реальности это не происходит ввиду того, что энергия электрических и магнитных полей, запасенных в реактивных элементах, не могут измениться скачком. Теоретически существование переходных процессов доказывается с помощью законов коммутации. Первый закон коммутации формулируется следующим образом: ток в индуктивности и потокосцепление не могут измениться скачком: где Допустим, что ток изменился скачком, тогда: следовательно, нарушается второй закон Кирхгофа, т.к. напряжение источника величина конечная, а падение напряжения на одном из участков цепи имеет бесконечно большую величину. Второй закон коммутации гласит: напряжение на емкости и заряд не могут измениться скачком, т.е.: В противном случае ток через емкость становится бесконечно большим: Это также приводит к нарушению второго закона Кирхгофа из-за возникновения бесконечно больших падений напряжений. Однако, скачкообразное изменение тока через емкость При расчете переходных процессов ток через индуктивность Пусть задана цепь с элементами Рис. 8.1. Схема исследуемой цепи Составим дифференциальное уравнение цепи после коммутации относительно тока: Полученное дифференциальное уравнение является неоднородным уравнением второго порядка. Решением данного уравнения является сумма двух решений: частного решения неоднородного уравнения и общего решения однородного. Частным решением (8.3) является ток, который назовем принужденной составляющей Если в послекоммутационной схеме отсутствуют источники энергии, то принужденные составляющие токов и напряжений будут равны нулю, и в цепи существует только свободный переходный процесс. Если дифференциальное уравнение составлено относительно какого - либо падения напряжения на участках цепи по рис. 8.1 , то его решение может быть представлено соответственно в виде: В зависимости от порядка решаемого дифференциального уравнения выделяют цепи первого, второго и высшего порядков, а сам порядок уравнения определяется количеством накопителей энергии, т.е. индуктивных и емкостных элементов. Рассмотрим методику расчета переходных процессов на примере цепи второго порядка (два накопителя энергии - катушка индуктивности и конденсатор). Рассчитывают докоммутациоииую схему и в полученных функциях индуктивного тока и емкостного напряжения определяют их численные значения в момент коммутации Для послекоммутационной схемы составляют систему уравнений по законам Кирхгофа и решают ее относительно искомого тока или напряжения. В полученном дифференциальном уравнении ЭДС источника приравнивают к нулю (получают однородное дифференциальное уравнение) и уже по виду этого уравнения составляют характеристическое уравнение, заменяя оператор дифференцирования Рассчитывают корни характеристического уравнения Записывают в общем виде решение дифференциального уравнения, например, для тока в какой-либо ветви схемы: Каждую из составляющих решения рассчитывают отдельно, а итоговое решение находят суммированием составляющих. Для определения принужденной составляющей тока нужно провести расчет схемы после коммутации в установившемся режиме. Решение для свободной составляющей тока ищется в виде: где В частности, при различных вещественных отрицательных корнях характеристического уравнения решение для свободной составляющей примет вид: Для расчета всех постоянных интегрирования это решение дифференцируют столько раз, чтобы общее число уравнений, включая уравнение (8.4), равнялось числу неизвестных. В нашем случае для определения и перепишем оба уравнения для момента времени В системе уравнений (8.5): а значение Необходимые зависимые начальные условия (в нашем случае Окончательно записывают решение для искомого тока или напряжения в виде суммы принужденной и свободной составляющих. Характеристическое уравнение можно получить разными способами. Составим для схемы рис. 8.2 систему уравнений по законам Кирхгофа относительно мгновенных значений токов и напряжений. Рис. 8.2. Электрическая цепь с двумя накопителями энергии Решим полученную систему уравнений, например, относительно тока it попутно примем ЭДС источника По виду однородного дифференциального уравнения составим характеристическое уравнение: Перепишем систему уравнений (8.6) относительно свободных токов и напряжений: Так как свободная составляющая тока изменяется по экспоненциальному закону: а производная и интеграл - это: то система уравнений (8.7) перепишется в виде: По виду системы (8.8) составим главный определитель системы: Поскольку все уравнения системы (8.8) равны нулю, то при расчете свободных составляющих токов любой из них определится как: Так как свободные токи не равны нулю, то принимают равным нулю определитель системы и тогда формально токи определяются решением неопределенностей Сравнение полученного выражения с характеристическим уравнением п. 8.3.1 показывает, что они одинаковы. Составим выражение для входного сопротивления цепи по переменному току: Произведем замену Получится выражение: Приравняем полученное уравнение к нулю Этот способ получит теоретическое обоснование в операторном методе расчета переходных процессов. Короткое замыкание цепи На рис. 8.3 представлена схема, в которой происходит короткое замыкание цепи с параметрами Рис. Короткое замыкание цепи Проиллюстрируем на примере этой цепи изложенную ранее методику расчета переходных процессов. 1. Рассчитаем схему до коммутации: 2. Составим дифференциальное уравнение исходной цепи после коммутации: По виду однородного дифференциального уравнения составляем характеристическое уравнение, заменяя оператор Можно получить тот же результат по выражению для входного сопротивления цепи по переменному току: Заменяем Такой способ удобнее применять в случае, когда переходный процесс происходит в сложной разветвленной цепи. Корень характеристического уравнения: Решение однородного дифференциального уравнения: где: 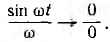 Раскрытие неопределенности
Раскрытие неопределенности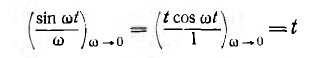
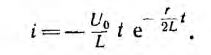
Включение цели на постоянное и переменное напряжение
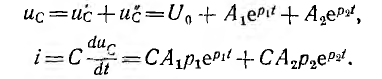
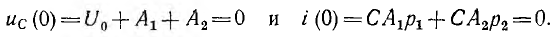
совпадают. Тогда постоянные интегрирования будут такими же, но имеющими обратный знак, а следовательно, свободные составляющие тока и напряжений при включении также будут отличаться от случая короткого замыкания только знаком. Тогда i и uL равны своим свободным составляющим i'' и u''L, напряжение же uс на емкости представляет собой сумму принужденной U0 и свободной u''с составляющих; поэтому на емкости в периодическом случае возникает перенапряжение, равное в пределе 2U0.Переходные процессы в сложных цепях
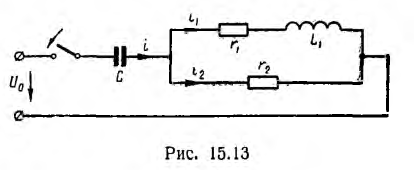
Пример расчета переходного процесса в сложной цепи
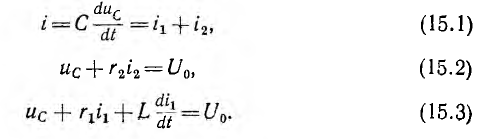
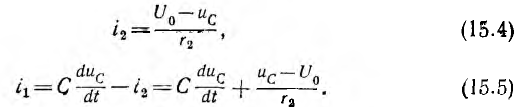
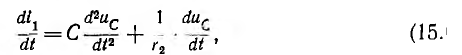
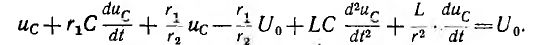
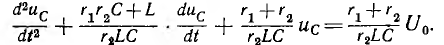
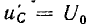 если характеристическое уравнение
если характеристическое уравнение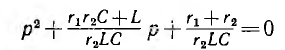
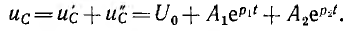
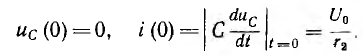
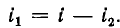 В зависимости от соотношения параметров возможен апериодический или колебательный процесс.
В зависимости от соотношения параметров возможен апериодический или колебательный процесс.Переходные процессы в цепях со взаимоиндукцией
0. Трансформатор нагружен индуктивностью и резистором (рис. 15.14). Система уравнений для первичной и вторичной цепи имеет вид: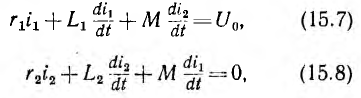
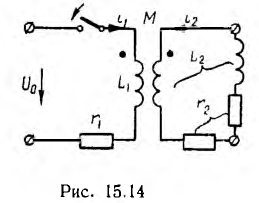
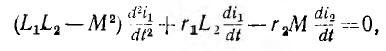
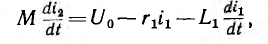
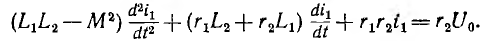
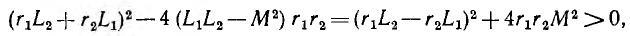
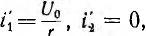 так как после установления в первичной цепи постоянного тока i'1 э. д. с. взаимоиндукции
так как после установления в первичной цепи постоянного тока i'1 э. д. с. взаимоиндукции 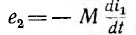 во вторичной цепи индуктироваться не будет.
во вторичной цепи индуктироваться не будет.Достоинства и недостатки классического метода
Переходные процессы в линейных цепях
Законы коммутации. Классический метод расчета переходных процессов
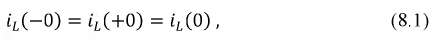
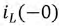 - значение тока через индуктивность непосредственно до коммутации;
- значение тока через индуктивность непосредственно до коммутации; 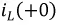 - значение тока через индуктивность сразу после коммутации, полагая, что сама коммутация происходит мгновенно.
- значение тока через индуктивность сразу после коммутации, полагая, что сама коммутация происходит мгновенно.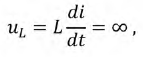
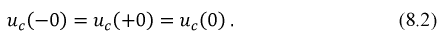
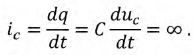
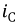 и падения напряжения на индуктивности
и падения напряжения на индуктивности 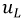 не приводят к нарушению электрического равновесия цепи, равно как и для параметров
не приводят к нарушению электрического равновесия цепи, равно как и для параметров 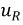 и
и 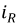
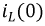 и напряжение на емкости
и напряжение на емкости 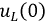 носят название независимых начальных условий. Все остальные токи и напряжения в момент коммутации являются зависимыми начальными условиями. Независимые начальные условия могут быть нулевыми и ненулевыми. Нулевые начальные условия соответствуют такому режиму работы цепи, когда к моменту коммутации токи во всех индуктивностях и падения напряжения на всех емкостях равны нулю. Если до коммутации какие-либо из этих величин не равны нулю, то начальные условия ненулевые. Независимые начальные условия характеризуют энергию, запасенную в соответствующих элементах к моменту коммутации.
носят название независимых начальных условий. Все остальные токи и напряжения в момент коммутации являются зависимыми начальными условиями. Независимые начальные условия могут быть нулевыми и ненулевыми. Нулевые начальные условия соответствуют такому режиму работы цепи, когда к моменту коммутации токи во всех индуктивностях и падения напряжения на всех емкостях равны нулю. Если до коммутации какие-либо из этих величин не равны нулю, то начальные условия ненулевые. Независимые начальные условия характеризуют энергию, запасенную в соответствующих элементах к моменту коммутации.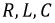 (рис. 8.1), в которой происходит коммутация (замыкание ключа).
(рис. 8.1), в которой происходит коммутация (замыкание ключа).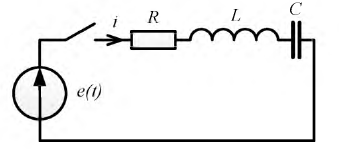
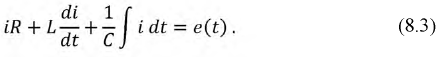
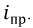 Это значение, к которому стремится ток при завершении переходного процесса. Он будет зависеть как от функции
Это значение, к которому стремится ток при завершении переходного процесса. Он будет зависеть как от функции 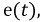 так и от параметров цепи. Общее решение - это функция, показывающая, по какому закону изменяется ток в отсутствии внешних источников энергии и зависящий от энергии электрического и магнитного полей, запасенной в индуктивных и емкостных элементах и обозначаемый как
так и от параметров цепи. Общее решение - это функция, показывающая, по какому закону изменяется ток в отсутствии внешних источников энергии и зависящий от энергии электрического и магнитного полей, запасенной в индуктивных и емкостных элементах и обозначаемый как 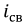 - свободная составляющая. На основании принципа наложения запишем:
- свободная составляющая. На основании принципа наложения запишем: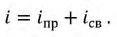
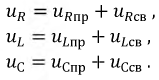
Общая методика расчета переходных процессов классическим методом
Определение независимых начальных условий
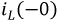 и
и 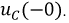
Составление характеристического уравнения
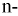 ого порядка на оператор
ого порядка на оператор 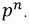
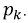
Определение принужденных токов и напряжений
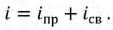
Определение свободных составляющих токов и напряжений
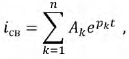
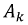 - постоянные интегрирования, рассчитываемые из начальных условий;
- постоянные интегрирования, рассчитываемые из начальных условий; 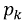 - корни характеристического уравнения.
- корни характеристического уравнения.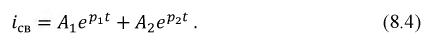
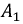 и
и 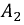 необходимо иметь два уравнения, поэтому продифференцируем уравнение (8.4) один раз, а именно:
необходимо иметь два уравнения, поэтому продифференцируем уравнение (8.4) один раз, а именно: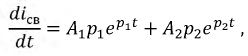
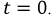
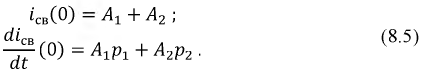
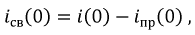
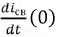 можно рассчитать через зависимые начальные условия, например, для схемы по рис. 8.1:
можно рассчитать через зависимые начальные условия, например, для схемы по рис. 8.1: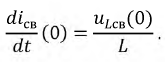
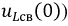 . Рассчитываются следующим образом: для послекоммутационной схемы составляется система уравнений по законам Кирхгофа относительно мгновенных значений токов и напряжений, полученную систему уравнений переписывают относительно свободных токов и напряжений, подставляют в нее найденные ранее независимые начальные условия и затем рассчитывают необходимые зависимые начальные условия.
. Рассчитываются следующим образом: для послекоммутационной схемы составляется система уравнений по законам Кирхгофа относительно мгновенных значений токов и напряжений, полученную систему уравнений переписывают относительно свободных токов и напряжений, подставляют в нее найденные ранее независимые начальные условия и затем рассчитывают необходимые зависимые начальные условия.Способы составления характеристического уравнения
Способ составления характеристического уравнения по виду дифференциального уравнения
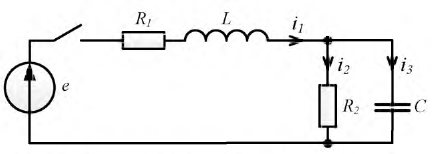
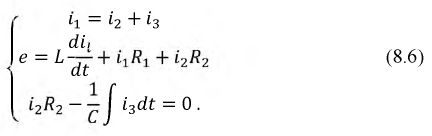
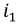 равным нулю, т.е. запишем решение относительно свободной составляющей тока:
равным нулю, т.е. запишем решение относительно свободной составляющей тока: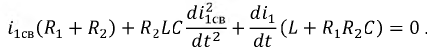
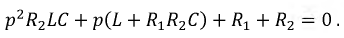
Способ составления характеристического уравнения по главному определителю системы уравнений
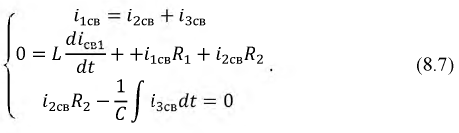
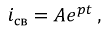
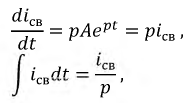
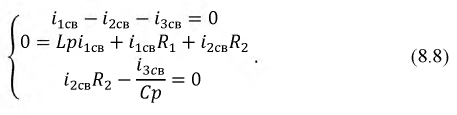
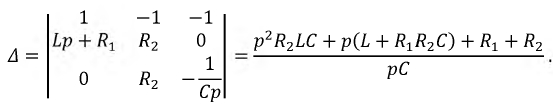
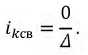
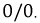 Главный определитель системы равный нулю и является характеристическим уравнением, а именно:
Главный определитель системы равный нулю и является характеристическим уравнением, а именно: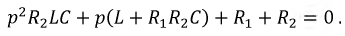
Составление характеристического уравнения по выражению для входного сопротивления цепи
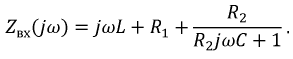

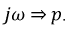
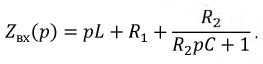
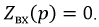 Это и есть характеристическое уравнение. В результате простых алгебраических преобразований характеристическое уравнение примет вид:
Это и есть характеристическое уравнение. В результате простых алгебраических преобразований характеристическое уравнение примет вид: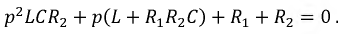
Переходный процесс в цепи
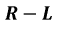
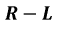
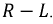
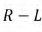
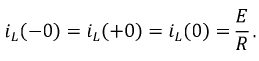
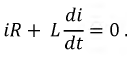
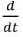 на
на 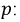
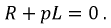
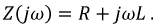
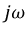 на
на 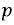 и приравняем полученное выражение к нулю:
и приравняем полученное выражение к нулю: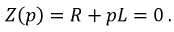
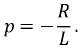
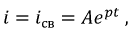
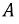 - некоторая постоянная интегрирования;
- некоторая постоянная интегрирования; 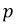 - корень характеристического уравнения.
- корень характеристического уравнения.
Определим постоянную 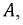 используя независимое начальное условие. Для момента времени
используя независимое начальное условие. Для момента времени 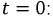
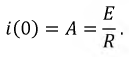
Окончательно решение примет вид:
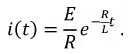
Проверка для тока:
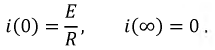
Рассчитаем падения напряжений на сопротивлении и индуктивности:
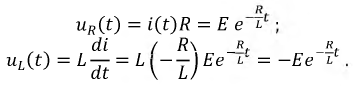
На основании второго закона Кирхгофа:
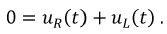
Проверка для падений напряжений:

Графики полученных выше функций представлены на рис. 8 .4.а, б.
Практическая длительность переходного процесса рассчитывается с помощью параметра, называемого постоянной времени 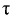 и определяется 1 как
и определяется 1 как 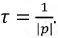 За время равное
За время равное 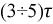 значение функции в переходном режиме достигает
значение функции в переходном режиме достигает 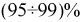 своего установившегося значения.
своего установившегося значения.
Найдем отношение:
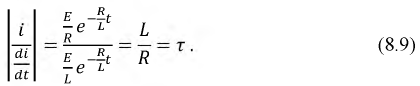
Это отношение показывает, что постоянная времени может быть определена графически следующим образом: проводится касательная к функции, например, тока 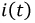 в любой её точке. В образовавшемся треугольнике
в любой её точке. В образовавшемся треугольнике 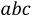 отрезок
отрезок 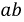 пропорционален току,
пропорционален току, 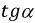 пропорционален производной функции
пропорционален производной функции 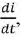 а их отношение на основании формулы (8.9) (отрезок или подкасательная
а их отношение на основании формулы (8.9) (отрезок или подкасательная 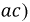 равняется постоянной времени
равняется постоянной времени 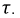
Рассчитаем энергию, выделившуюся в виде тепла в сопротивлении 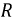 за время переходного процесса:
за время переходного процесса:
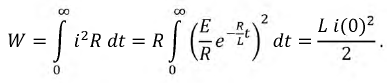
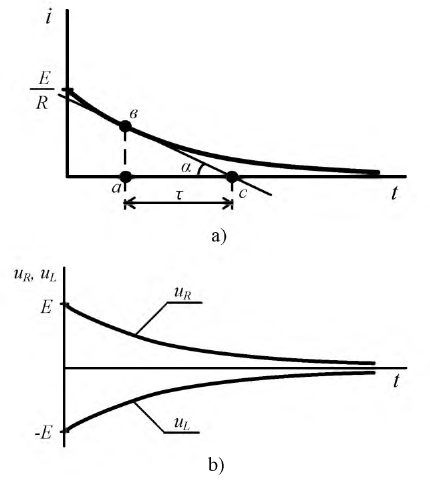
Рис. 8.4. Графики изменения в переходном процессе (а) - тока 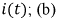 - падений напряжений
- падений напряжений 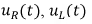
Полученный результат представляет энергию, запасенную индуктивностью к моменту коммутации.
Подключение цепи 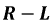 к источнику постоянной ЭДС:
к источнику постоянной ЭДС:
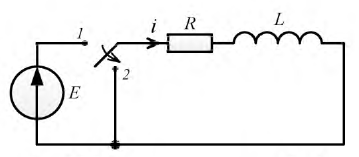
Пусть катушка индуктивности подключена к источнику постоянного напряжения (рис. 8.5).
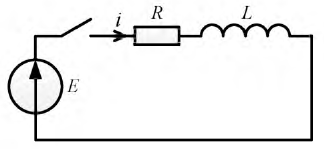
Рис. 8.5. Схема включения катушки к источнику постоянного напряжения
Проведем расчет переходного процесса в этой цепи.
1. Расчет независимых начальных условий:
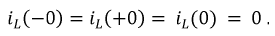
2. Дифференциальное уравнение, описывающее цепь после коммутации:
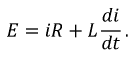
На основании однородного дифференциального уравнения составим характеристическое уравнение:
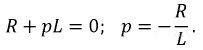
3. Общее решение неоднородного дифференциального уравнения имеет вид:
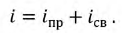
Принужденный ток:
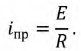
Свободный ток:
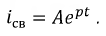
Тогда полное решение примет вид:
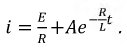
Для получения окончательного решения необходимо рассчитать постоянную интегрирования 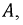 воспользовавшись для этого независимыми начальными условиями. При
воспользовавшись для этого независимыми начальными условиями. При 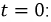
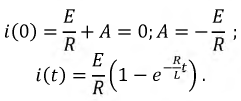
Проверка:
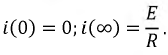
Используя полученную функцию для тока, найдем функции 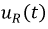 и
и 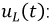
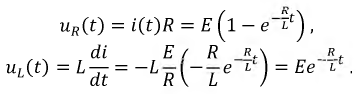
Проверка:
Используя второй закон Кирхгофа, проверим правильность результатов:
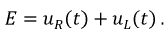
Для данных нулевых начальных условий можно сказать, что индуктивность в момент коммутации может быть представлена разрывом. По найденным функциям построим соответствующие графики (рис. 8.6).
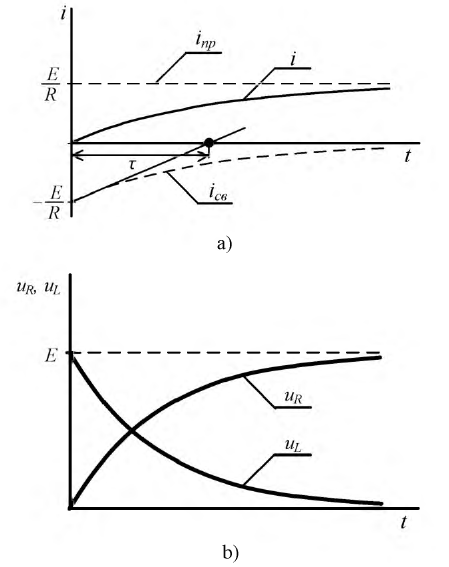
Рис. 8.6. Графики изменения в переходном процессе (а) - тока 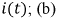 - падений напряжений
- падений напряжений 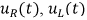
Подключение цепи  к источнику синусоидального напряжения:
к источнику синусоидального напряжения:
Пусть входное напряжение изменяется по закону:
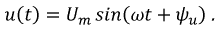
Так как цепь та же (см. рис. 8.5), то она описывается тем же дифференциальным уравнением. Следовательно, начальные условия и решение уравнения в общем виде не изменились:
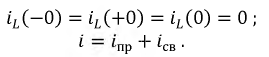
Однако принужденная составляющая изменилась, т.к. на входе цепи действует синусоидальный источник напряжения:
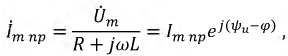
где:
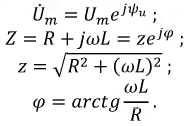
Мгновенное значение принужденного тока примет вид:
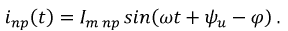
Полный ток равен:
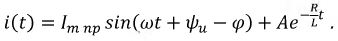
Из начальных условий (при 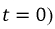 найдем значение
найдем значение 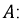
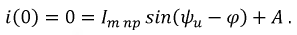
Откуда:
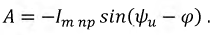
Запишем окончательное выражение для тока в переходном режиме:
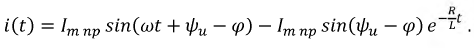
Проверка:
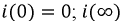 - периодическая функция тока.
- периодическая функция тока.
Используя полученную функцию тока 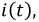 можно рассчитать законы изменения напряжений на индуктивности
можно рассчитать законы изменения напряжений на индуктивности 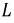 и сопротивлении
и сопротивлении 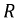 по соответствующим выражениям:
по соответствующим выражениям:
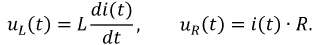
Построим график найденной функции тока и рассмотрим ряд вариантов, связанных с величиной параметров 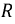 и
и 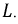
1 вариант:
Пусть 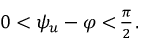
В первом полупериоде после коммутации значение тока превышает амплитуду его установившейся составляющей (рис. 8.7).
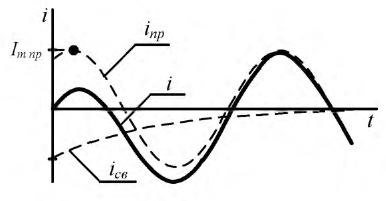
Рис. 8.7. График тока в катушке при синусоидальном источнике напряжения
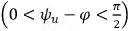
2 вариант:
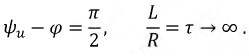
Если катушка обладает параметрами, при которых 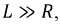 то ток в переходном процессе в момент времени
то ток в переходном процессе в момент времени 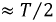 почти в 2 раза превышает амплитуду установившегося тока (рис. 8 .8 ). Это значение тока превышает уставку тока аппаратуры защиты, и она может сработать и отключить катушку (трансформатор, дроссель и т.д.) от сети.
почти в 2 раза превышает амплитуду установившегося тока (рис. 8 .8 ). Это значение тока превышает уставку тока аппаратуры защиты, и она может сработать и отключить катушку (трансформатор, дроссель и т.д.) от сети.
3 вариант:
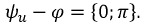
Свободная составляющая тока равна нулю и в цепи с момента коммутации существует только установившийся ток (рис. 8.9).
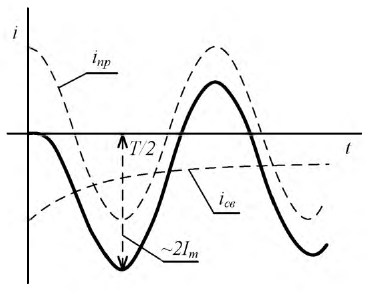
Рис. 8.8. График тока в катушке при синусоидальном источнике напряжения 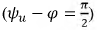
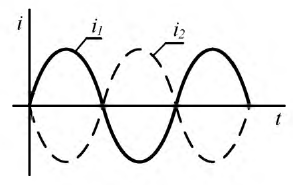
Рис. 8.9. График тока в катушке при синусоидальном источнике напряжения: 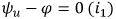 и
и 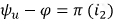
Переходный процесс в цепи R-C
8.5.1. Короткое замыкание цепи 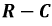
На рис. 8-10 представлена схема, в которой происходит короткое замыкание цепи с параметрами 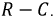
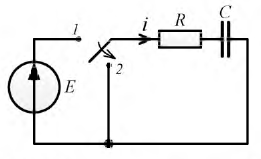
Рис. 8.10. Короткое замыкание цепи 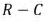
1. Рассчитаем независимые начальные условия. До коммутации при работе схемы от источника постоянной ЭДС конденсатор был заряжен до величины 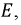 т.е.:
т.е.:
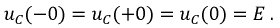
2. Составим дифференциальное уравнение для цепи после коммутации по 2-му закону Кирхгофа:
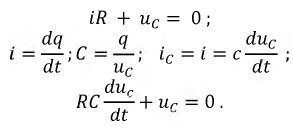
Т.к. дифференциальное уравнение однородное, то по его виду можно сразу составить характеристическое уравнение:
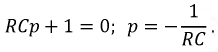
3. Решение данного уравнения имеет вид:
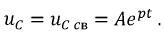
Определим постоянную интегрирования 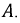 При
При 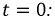
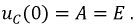
Окончательно:
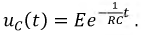
Проверка:
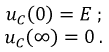
Используя найденную функцию напряжения, определим ток и падение напряжения на активном сопротивлении:
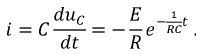
Если 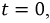 то
то 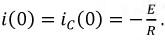
Знак минус говорит о том, что разрядный ток в цепи 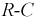 направлен встречно зарядному:
направлен встречно зарядному:
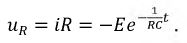
Проверка:
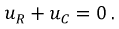
На рис. 8.11 и рис. 8.12 построены соответственно графики 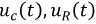 и
и 
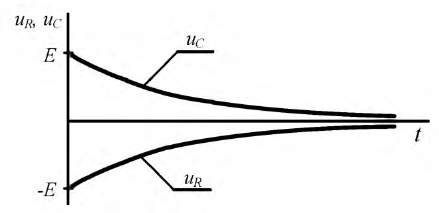
Рис. 8.11. Графики 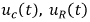 при разряде конденсатора
при разряде конденсатора

Рис. 8.12. График разрядного тока  в цепи
в цепи 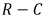
Вновь оценим энергетику переходного процесса в цепи 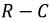 подобно цепи
подобно цепи 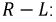
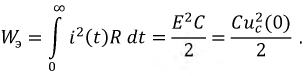
Тепловые потери в резисторе в течение переходного процесса равны накопленной в конденсаторе энергии электрического поля.
Подключение цепи 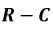 к источнику постоянной ЭДС:
к источнику постоянной ЭДС:
Пусть цепь 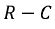 подключена к источнику постоянного напряжения
подключена к источнику постоянного напряжения 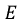 (рис. 8.13).
(рис. 8.13).
Проведем расчет переходного процесса.
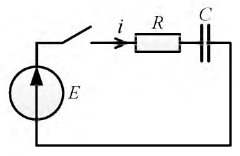
Рис. 8.13. Подключение цепи 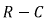 к источнику постоянного напряжения
к источнику постоянного напряжения
1. Расчет независимых начальных условий:
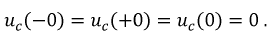
2. Дифференциальное уравнение цепи имеет вид:
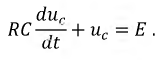
Если правую часть уравнения принять равной нулю, то получим однородное дифференциальное и, соответственно, характеристическое уравнение п. 8.5.1, следовательно,
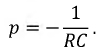
3. Полное решение неоднородного дифференциального уравнения имеет вид:
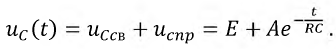
Принужденная составляющая напряжения:
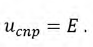
Свободная составляющая изменяется по закону:
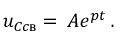
При 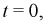 получим:
получим: 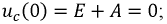 тогда
тогда 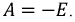
В итоге напряжение на конденсаторе изменяется по закону:
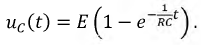
Проверка:
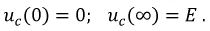
Зарядный ток конденсатора изменяется по закону:
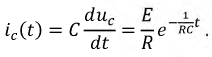
Падение напряжения на резисторе:
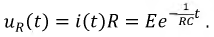
По второму закону Кирхгофа имеем:
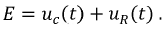
На рис. 8.14 представлен график переходного процесса напряжения на конденсаторе при его зарядке от источника постоянного напряжения.
Постоянная времени цепи 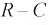 будет:
будет:
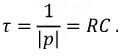
Графически ее можно определить так же, как и для цепи 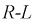 (см. рис. 8.4.а).
(см. рис. 8.4.а).
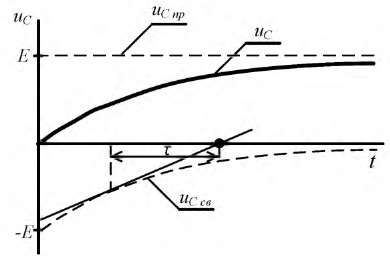
Рис. 8.14. Закон изменения напряжения на конденсаторе при его подключении к источнику постоянного напряжения
В момент коммутации конденсатор может быть заменен короткозамкнутым проводником: 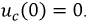
Если активное сопротивление такой цепи мало, ток в момент коммутации может достигать значительных величин.
Подключение цепи 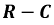 к источнику синусоидального напряжения:
к источнику синусоидального напряжения:
Пусть ЭДС источника изменяется по закону:
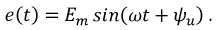
1 .Начальные условия:
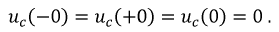
2. Характеристическое уравнение и его корень:
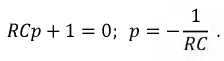
3. Определим функцию тока в установившемся режиме:
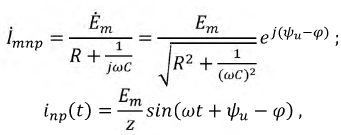
где:
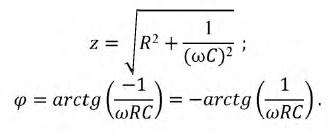
По полученной функции тока рассчитаем принужденную составляющую напряжения на емкости:
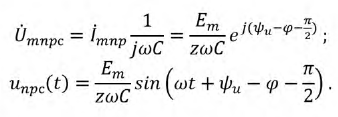
Общее решение для напряжения на емкости представляет собой сумму принужденной и свободной составляющих:
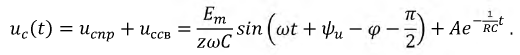
Для определения постоянной 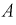 используем начальные условия:
используем начальные условия:
Пусть 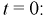
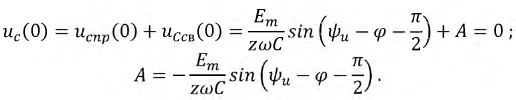
Запишем окончательное выражение для напряжения на емкости в переходном режиме:
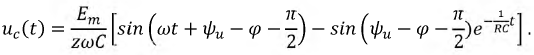
Проверка: 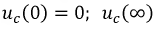 - периодическая функция напряжения на конденсаторе.
- периодическая функция напряжения на конденсаторе.
Построим график функции 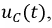 приняв, что
приняв, что 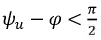 (рис. 8.15).
(рис. 8.15).
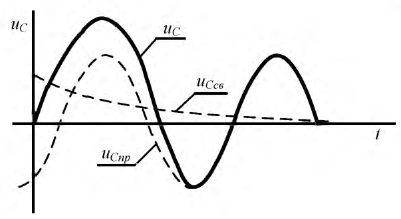
Рис. 8.15. Напряжение на емкости в переходном процессе при подключении цепи 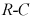 к источнику синусоидального напряжения
к источнику синусоидального напряжения
Максимальное напряжение на емкости в переходном процессе при 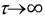 может достигнуть двукратной величины амплитуды установившегося режима. Это произойдет в случае, когда начальная фаза напряжения на емкости
может достигнуть двукратной величины амплитуды установившегося режима. Это произойдет в случае, когда начальная фаза напряжения на емкости 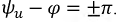 В то же время, если
В то же время, если 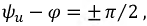 то переходный процесс в такой цепи будет отсутствовать, т.е. после коммутации в цепи сразу возникает установившийся режим.
то переходный процесс в такой цепи будет отсутствовать, т.е. после коммутации в цепи сразу возникает установившийся режим.
Переходный процесс в цепи с двумя накопителями энергии
Процессы, возникающие в цепях такого рода, существенным образом отличаются от процессов в цепях с одним накопителем энергии, которые были рассмотрены выше.
На рис. 8.16 представлена схема, в которой происходит короткое замыкание цепи с параметрами 
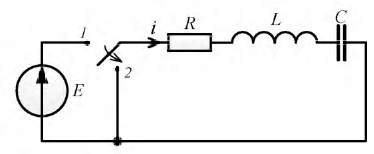
Рис. 8.16. Электрическая цепь с двумя накопителями энергии
1. Независимые начальные условия:
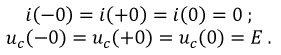
2. Для цепи после коммутации интегрально-дифференциальное уравнение по второму закону Кирхгофа:
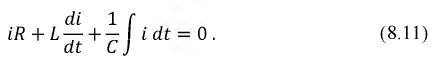
Дифференцируя (8.11), получим уравнение второго порядка относительно тока:
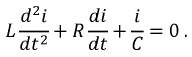
По виду однородного дифференциального уравнения составим характеристическое уравнение:
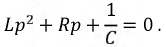
Его решение имеет вид:
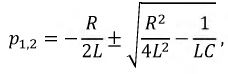
где 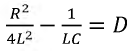 - дискриминант характеристического уравнения.
- дискриминант характеристического уравнения.
Исходя из значений дискриминанта 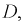 переходный процесс в цепи может развиваться по одному из трех вариантов, т.е. быть апериодическим
переходный процесс в цепи может развиваться по одному из трех вариантов, т.е. быть апериодическим 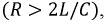 колебательным
колебательным 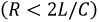 или иметь предельный (критический) характер
или иметь предельный (критический) характер 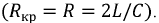
Апериодический переходный процесс
Апериодический переходный процесс возникает при условии, когда дискриминант 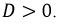 В схеме по рис. 8.16
В схеме по рис. 8.16 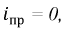 тогда:
тогда:
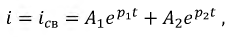
где: 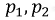 вещественные отрицательные корни;
вещественные отрицательные корни;
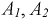 — неизвестные постоянные интегрирования.
— неизвестные постоянные интегрирования.
Для определения двух неизвестных 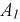 и
и 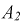 необходимо составить еще одно уравнение. Его можно получить, дифференцируя исходное (8.11а):
необходимо составить еще одно уравнение. Его можно получить, дифференцируя исходное (8.11а):
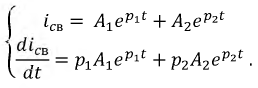
Далее воспользуемся независимыми начальными условиями. Полагая 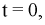 получим:
получим:
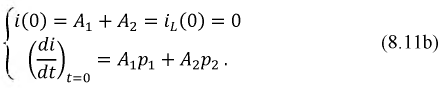
где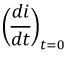 - зависимое начальное условие, определение которого и составляет основную сложность расчета переходных процессов классическим методом.
- зависимое начальное условие, определение которого и составляет основную сложность расчета переходных процессов классическим методом.
Общий подход по определению таких условий состоит в совместном использовании законов Кирхгофа и законов коммутации.
Для его реализации используем известные соотношения для функций 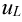 и
и 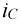 и преобразуем их, приняв
и преобразуем их, приняв 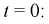
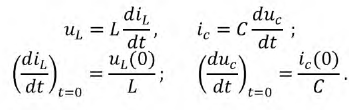
Тогда второе уравнение системы (8.11b) примет вид:
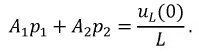
Однако и 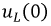 также является зависимым начальным условием.
также является зависимым начальным условием.
По второму закону Кирхгофа получим:
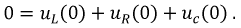
Так как:
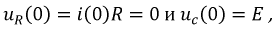
получим:
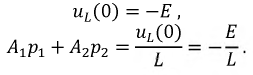
Таким образом, для определения двух неизвестных 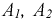 получили систему из двух уравнений:
получили систему из двух уравнений:
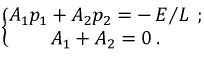
Ее решение дает значения 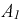 и
и 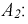
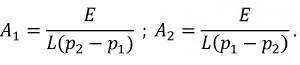
Итоговое выражение функции тока переходного процесса примет вид:
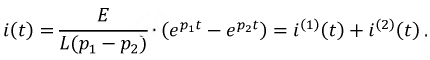
На рис. 8.17 представлен график тока при апериодическом переходном процессе в цепи второго порядка.
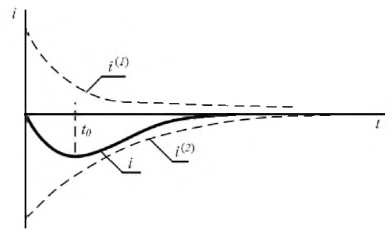
Рис. 8.17. График тока 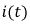 при апериодическом переходном процессе
при апериодическом переходном процессе
Из рис. 8.17 следует, что спустя некоторое время 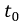 после момента коммутации, значение тока достигает максимума.
после момента коммутации, значение тока достигает максимума.
Используя функцию тока 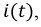 найдем напряжения
найдем напряжения 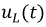 и
и 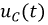 в переходном процессе.
в переходном процессе.
Падение напряжения на индуктивности:
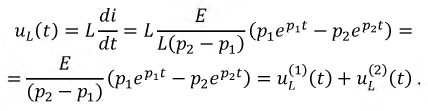
В момент времени 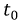 функция меняет знак и ее значение равно нулю (рис. 8.18), что соответствует максимуму функции тока, полученной выше.
функция меняет знак и ее значение равно нулю (рис. 8.18), что соответствует максимуму функции тока, полученной выше.
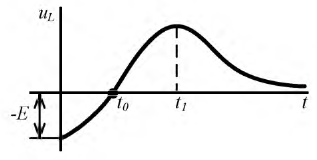
Рис. 8.18. График 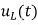 при апериодическом переходном процессе
при апериодическом переходном процессе
Падение напряжения на емкости:
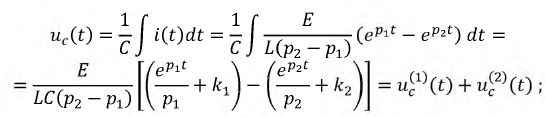
где 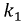 и
и 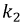 - неизвестные постоянные интегрирования, которые определим из начальных условий.
- неизвестные постоянные интегрирования, которые определим из начальных условий.
При 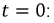
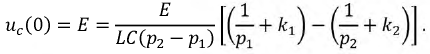
Так как:
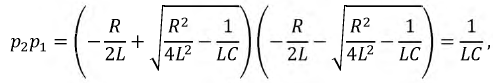
то:
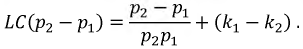
Таким образом, 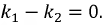
В итоге имеем функцию падения напряжения на емкости в виде:
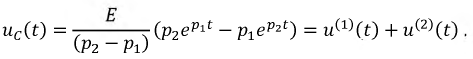
График функции 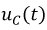 приведен на рис. 8.19.
приведен на рис. 8.19.
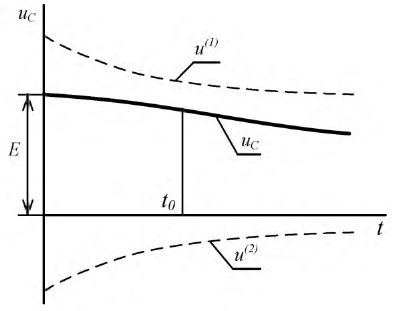
Рис. 8.19. График напряжения на конденсаторе при апериодическом переходном процессе
Рассмотрим энергетику апериодического переходного процесса.
В короткозамкнутом контуре (см. рис. 8.16) происходит разряд конденсатора на цепь 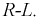 В течение всего переходного процесса
В течение всего переходного процесса 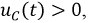
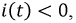 следовательно, мгновенная мощность
следовательно, мгновенная мощность 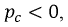 т.е. емкость только лишь отдает в цепь энергию, запасенную в его электрическом поле. Резистивный элемент только потребляет мощность
т.е. емкость только лишь отдает в цепь энергию, запасенную в его электрическом поле. Резистивный элемент только потребляет мощность 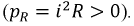 На индуктивности в интервале времени
На индуктивности в интервале времени 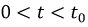 энергия магнитного поля накапливается, а начиная с момента
энергия магнитного поля накапливается, а начиная с момента 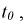 начинает расходоваться, выделяясь в виде тепла на резистивном элементе.
начинает расходоваться, выделяясь в виде тепла на резистивном элементе.
Колебательный (периодический) переходный процесс
Предположим, что в той же цепи (см. рис. 8.16) параметры 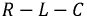 таковы, что дискриминант
таковы, что дискриминант 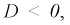 при этом корни характеристического уравнения становятся комплексно сопряженными:
при этом корни характеристического уравнения становятся комплексно сопряженными:
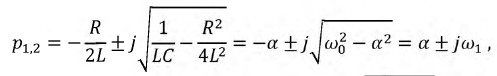
где 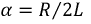 - коэффициент затухания;
- коэффициент затухания; 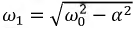 - частота свободных колебаний
- частота свободных колебаний 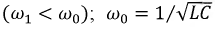
Общим решением исходного дифференциального уравнения (8.11), записанного относительно напряжения на емкости,
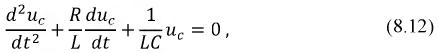
будет функция:
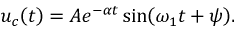
Амплитуда синусоиды убывает по экспоненциальному закону.
Неизвестными в данном случае являются параметры 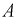 и
и 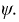 Принцип их определения тот же: первое уравнение - это исходное решение для
Принцип их определения тот же: первое уравнение - это исходное решение для 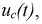 второе уравнение получаем дифференцированием первого, а именно:
второе уравнение получаем дифференцированием первого, а именно:
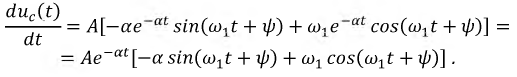
Для определения 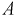 и
и 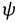 вновь воспользуемся начальными условиями, (независимыми и зависимыми):
вновь воспользуемся начальными условиями, (независимыми и зависимыми):
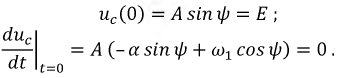
Окончательно система уравнений примет вид:
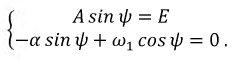
Её решение дает:
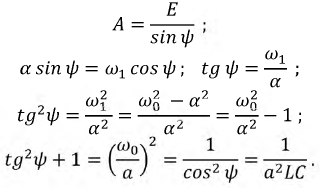
Отсюда:
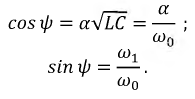
Тогда:
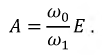
Запишем окончательно решение для напряжения на емкости:
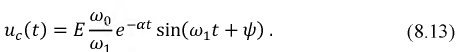
Данная функция представлена на рис. 8.20.
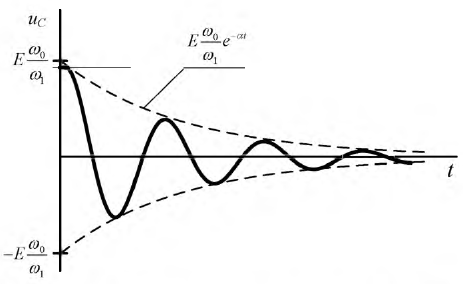
Рис. 8.20. Функция 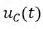 в колебательном переходном процессе
в колебательном переходном процессе
В случае, когда затухание в контуре отсутствует 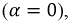 уравнение (8.13) упростится:
уравнение (8.13) упростится:
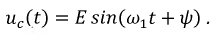
При 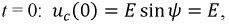 тогда
тогда 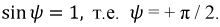
По найденной функции 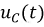 можно определить функцию тока в данной цепи, которая может быть записана в виде:
можно определить функцию тока в данной цепи, которая может быть записана в виде:
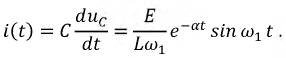
График функции 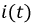 изображен на рис. 8.21.
изображен на рис. 8.21.
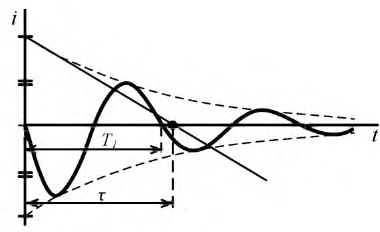
Рис. 8.21. Функция тока 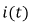 в колебательном переходном процессе
в колебательном переходном процессе
Проверка:
При 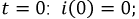
При 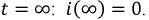
По аналогии с цепями 1-го порядка здесь также можно графически определить постоянную времени 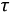 переходного процесса. Для определения постоянной времени проведем касательную к огибающей и измерим длину подкасательной.
переходного процесса. Для определения постоянной времени проведем касательную к огибающей и измерим длину подкасательной.
Функции 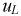 и
и 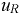 могут быть получены с использованием вновь полученных функций
могут быть получены с использованием вновь полученных функций 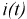 и
и 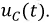
С физической точки зрения колебательный характер переходного процесса свидетельствует о том, что между индуктивностью и емкостью происходит обмен энергией при одновременном рассеивании ее части в сопротивлении 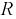 в виде тепла. Подобного рода картина не имеет место при апериодическом процессе, там такого обмена нет по причине большого затухания в контуре.
в виде тепла. Подобного рода картина не имеет место при апериодическом процессе, там такого обмена нет по причине большого затухания в контуре.
Помимо таких параметров, как 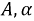 и
и 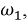 в цепях 2-го порядка вводится параметр, характеризующий скорость затухания переходного процесса.
в цепях 2-го порядка вводится параметр, характеризующий скорость затухания переходного процесса.
Это декремент затухания:
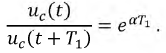
Логарифмируя заданное выражение получим:
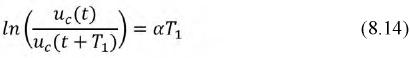
Анализ цепей синусоидального тока в установившемся режиме показывает, что ток или напряжение могут быть изображены на комплексной плоскости в виде некоторого вектора, который вращается с частотой задающего генератора 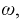 начиная с некоторой начальной фазы
начиная с некоторой начальной фазы 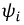 (рис. 8 .2 2 ).
(рис. 8 .2 2 ).
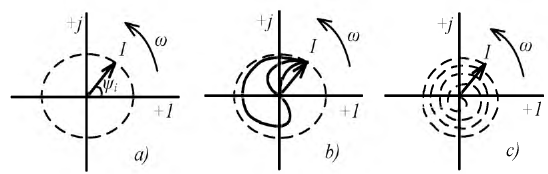
Рис. 8.22. Годографы вектора тока при: а) отсутствии затуханий; b) значительном затухании 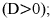 с) малом затухании
с) малом затухании 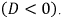
Критический случай апериодического переходного процесса
Будем считать, что в схеме, представленной на рис. 8.16, параметры 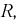
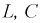 подобраны так, что
подобраны так, что 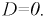 Условия работы цепи не изменились. Таким образом, в цепи по-прежнему существует лишь свободный переходный процесс, поэтому корни характеристического уравнения (см.8.11а) не изменились.
Условия работы цепи не изменились. Таким образом, в цепи по-прежнему существует лишь свободный переходный процесс, поэтому корни характеристического уравнения (см.8.11а) не изменились.
Однако, если 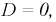 то:
то:
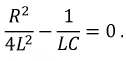
Следовательно,
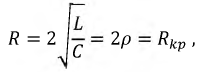
где 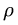 - волновое сопротивление контура по рис. 8.16,
- волновое сопротивление контура по рис. 8.16, 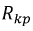 - критическое сопротивление.
- критическое сопротивление.
Понятие критического сопротивления контура 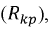 определяет границу, которая разделяет два качественно разных переходных процесса данной цепи: апериодический и колебательный.
определяет границу, которая разделяет два качественно разных переходных процесса данной цепи: апериодический и колебательный.
При 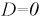 имеем:
имеем:
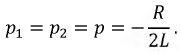
В связи с этим общее решение дифференциального уравнения (8.12) имеет вид:
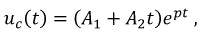
где 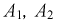 - по-прежнему неизвестные постоянные, подлежащие определению. Для их нахождения составим еще одно уравнение путем дифференцирования:
- по-прежнему неизвестные постоянные, подлежащие определению. Для их нахождения составим еще одно уравнение путем дифференцирования:
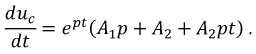
Для определения 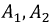 используем начальные условия:
используем начальные условия:
При 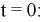
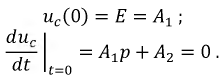
Так как:
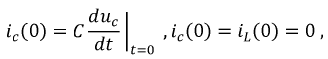
то:
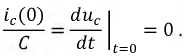
Вновь получим систему с двумя неизвестными:
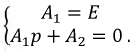
Ее решение позволит получить искомую функцию 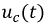 в виде:
в виде:

Используя полученное выражение, аналогичным образом определим функции 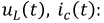
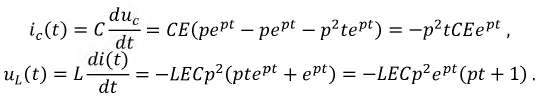
Проверка:
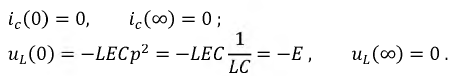
Графики полученных функций строятся аналогично.
Переходные процессы при скачкообразном изменении параметров
В электрической цепи возможны такие ситуации, когда индуктивность, емкость или сопротивление в момент коммутации изменяются скачком. Скачкообразное изменение сопротивления не приведет к изменению независимых начальных условий, и, следовательно, к нарушению законов коммутации, а изменение индуктивности или емкости однозначно вызовет нарушение законов коммутации, т.к. это приведет к скачкообразному изменению энергии, запасенной к моменту коммутации в индуктивных и емкостных элементах. Выясним, как вести расчет переходных процессов при некорректных начальных условиях.
Скачкообразное изменение индуктивности.
На схеме рис. 8.23 показан вариант изменения индуктивности в момент коммутации от величины 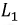 до
до 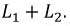
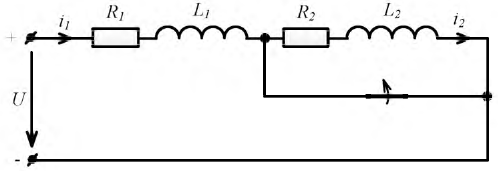
Рис. 8.23. Схема, иллюстрирующая скачкообразное изменение индуктивности
Величины токов в обеих индуктивностях до коммутации соответственно равны:
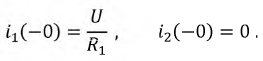
После коммутации обе индуктивности соединены последовательно и ток в них одинаков. Следовательно, в момент коммутации ток в 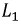 и
и 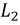 изменился скачком, что противоречит первому закону коммутации. Сформулируем условия, которым соответствует переходный процесс в рассматриваемой схеме.
изменился скачком, что противоречит первому закону коммутации. Сформулируем условия, которым соответствует переходный процесс в рассматриваемой схеме.
Уравнение электрического равновесия для послекоммутационной схемы имеет вид:
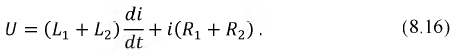
Характеристическое уравнение для исследуемой цепи:
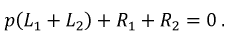
Корень характеристического уравнения равен:
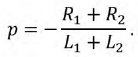
Ток в переходном режиме ищем в виде суммы двух слагаемых:
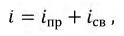
где:
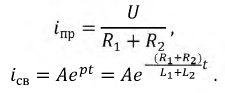
Сложность задачи заключается в определении постоянной интегрирования 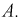
Так как оба тока изменились скачком, то теоретически падения напряжения на обеих катушках стали бесконечно большими, но с разными знаками, так как первый ток уменьшился, а второй увеличился.
При этом в уравнении (8.16) напряжением сети и падениями напряжения на обоих сопротивлениях по сравнению с бесконечно большими падениями напряжения на индуктивностях можно пренебречь. Тогда уравнение равновесия цепи (8.16) примет вид:
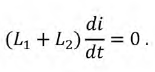
Проинтегрируем полученное уравнение по времени:
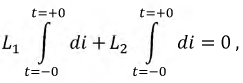
или:
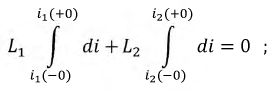
откуда:
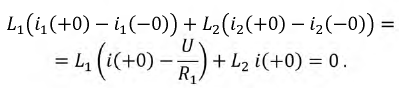
В этом уравнении в первом и втором слагаемом указаны скачки тока, поэтому перепишем его в следующей форме:
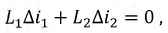
или:

Полученное выражение (8.17) представляет собой первый закон коммутации в обобщенной форме, то есть, суммарное потокосцепление в момент коммутации не может измениться скачком.
Из полученного уравнения рассчитаем ток 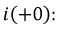
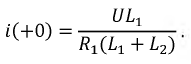
Перепишем решение уравнения для момента коммутации:
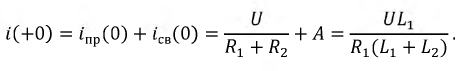
Постоянная 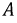 примет вид:
примет вид:
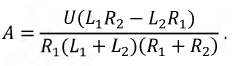
И, наконец, окончательное решение для тока в переходном режиме:
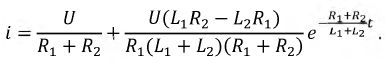
На рис. 8.24 приведен график полученной функции 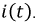
Рис. 8.24. График тока в переходном режиме при скачкообразном изменении индуктивности
Необходимо отметить, что энергия, запасенная в индуктивности 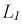 к моменту коммутации, не равна энергии обеих катушек сразу после коммутации:
к моменту коммутации, не равна энергии обеих катушек сразу после коммутации:
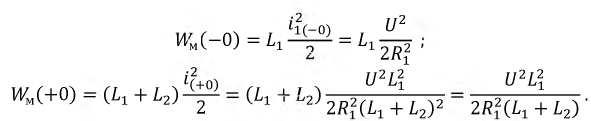
То есть:
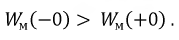
Формально полученное соотношение противоречит законам коммутации, но необходимо учесть, что сама коммутация происходит в течение пусть очень малого, но конечного времени, за которое сопротивление контактов ключа меняется от нуля до бесконечности или, наоборот. Кроме того, переходному процессу соответствует теоретически бесконечный частотный спектр и на высоких частотах происходит излучение части энергии в пространство.
Скачкообразное изменение емкости.
Допустим, что в схеме рис. 8.25 в момент коммутации емкость возрастет от значения 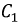 до
до 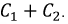
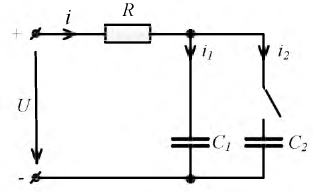
Рис. 8.25. Схема со скачкообразным изменением емкости
Рассчитаем напряжение на емкости в переходном режиме.
До коммутации напряжения на емкостях равнялись:
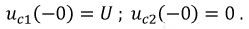
Уравнения электрического равновесия для послекоммутационной схемы:
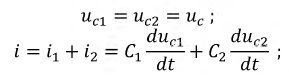
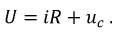
При совместном решении этих уравнений получаем дифференциальное уравнение цепи:
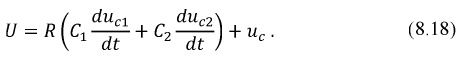
Тогда характеристическое уравнение примет вид:
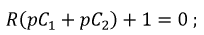
и его корень
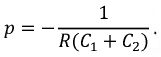
Решение дифференциального уравнения относительно напряжения на емкости ищем в форме:
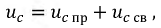
где
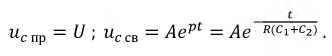
Рассчитаем постоянную интегрирования 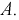
В уравнении (8.18) токи 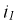 и
и 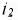 теоретически принимают бесконечно большие значения из-за скачкообразных изменений напряжений на ёмкостях, поэтому током
теоретически принимают бесконечно большие значения из-за скачкообразных изменений напряжений на ёмкостях, поэтому током 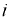 по сравнению с ними можно пренебречь, т.е.:
по сравнению с ними можно пренебречь, т.е.:
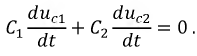
Проинтегрируем полученное уравнение по времени:
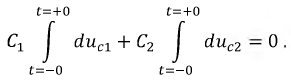
В результате получим уравнение:
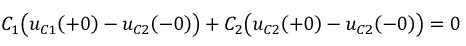
или:
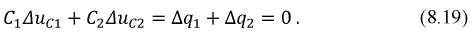
Уравнение 8.19 соответствует второму закону коммутации в обобщённой форме: суммарный заряд конденсаторов в процессе коммутации остается неизменным.
Графики напряжений на емкостях в переходном режиме представлены на рис. 8.26.
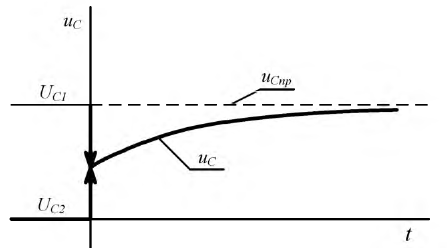
Рис. 8.26. Графики падений напряжений на емкостях 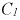 и
и 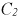 в переходном режиме
в переходном режиме
Пример расчета переходных процессов в цепи  классическим методом
классическим методом
Пусть дана цепь (рис. 8.27):
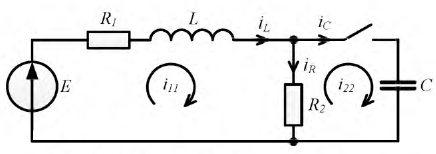
Рис. 8.27. Цепь с двумя накопителями энергии
Исходные параметры цепи:
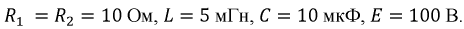
Определить ток 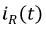
1. Производится расчет режима работы цепи до коммутации, и определяются независимые начальные условия 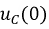 и
и 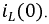
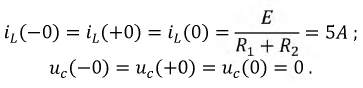
2. Составляется система дифференциальных уравнений, описывающая процесс в цепи после коммутации. Используя метод контурных токов, получим следующую систему уравнений:
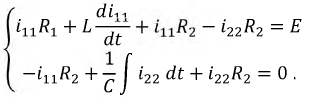
Разобьем данную систему на две:
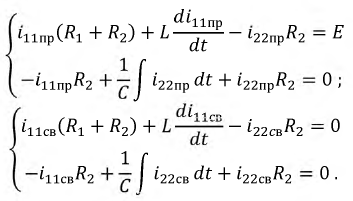
Используя систему уравнений для свободных составляющих токов, составим характеристическое уравнение цепи и найдем его корни:
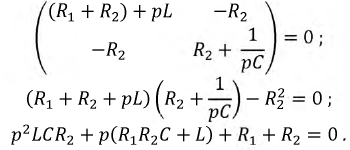
После подстановки исходных данных приведенное квадратное уравнение примет вид:
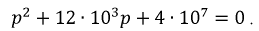
Корни уравнения получились комплексно сопряженными:
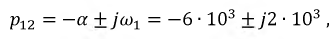
а значит, переходный процесс развивается по колебательному закону.
3. Так как решением исходной системы является сумма двух слагаемых, общего и частного, то отдельно определяют принужденные и свободные составляющие искомых токов и напряжений в переходном процессе.
Ток 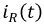 целесообразно рассчитать через напряжение на емкости, а именно:
целесообразно рассчитать через напряжение на емкости, а именно:
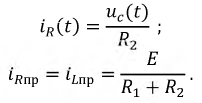
Тогда принужденная составляющая напряжения на емкости будет:
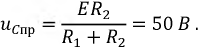
4. Свободную составляющую напряжения на емкости запишем в виде:
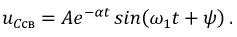
Для определения двух неизвестные величин 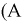 и
и 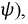 составим второе уравнение путем дифференцирования
составим второе уравнение путем дифференцирования 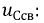
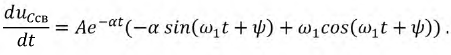
Перепишем оба равнения для момента коммутации:
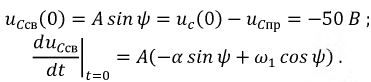
Рассчитаем зависимое начальное условие 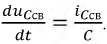 Для этого составим систему уравнений по законам Кирхгофа относительно свободных составляющих токов и напряжений, подставим в них найденные ранее независимые начальные условия и определим необходимые зависимые начальные условия:
Для этого составим систему уравнений по законам Кирхгофа относительно свободных составляющих токов и напряжений, подставим в них найденные ранее независимые начальные условия и определим необходимые зависимые начальные условия:
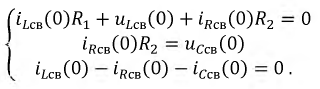
Свободная составляющая тока через индуктивность:
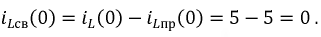
Тогда:
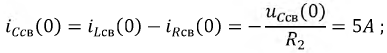
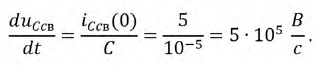
Запишем полученную систему уравнений относительно постоянных интегрирования:
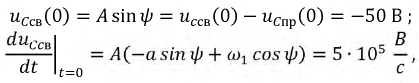
откуда:
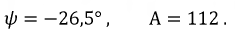
Суммируя принужденные и свободные составляющие, определим функцию 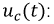
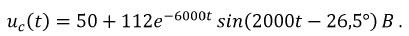
Искомое значение функции 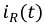 будет:
будет:
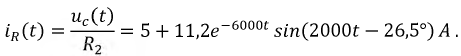
Операторный метод расчета переходных процессов
Наряду с классическим методом расчета переходных процессов операторный метод нашел весьма широкое практическое применение, обусловленное известными преимуществами. Основная сложность расчета классическим методом состоит в определении постоянных интегрирования. По мере возрастания сложности электрических цепей и, следовательно, порядка дифференциальных уравнений существенно усложняется задача по расчету этих постоянных интегрирования. В основе операторного метода лежит замена системы дифференциальных уравнений системой алгебраических уравнений, расчет которой значительно проще. Решение поставленной задачи осуществляется с помощью известного преобразования Лапласа. Основная идея этого преобразования состоит в том, что некоторой реальной функции времени 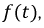 где
где 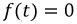 при
при 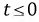 ставится в соответствие другая функция комплексного переменного
ставится в соответствие другая функция комплексного переменного 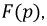 где
где 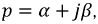 т.е.:
т.е.:
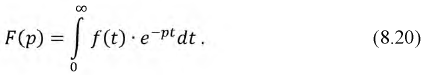
Причем 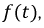 - оригинал функции, a
- оригинал функции, a 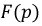 - ее изображение.
- ее изображение.
Математически связь между оригиналом и изображением представляется в форме:
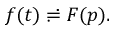
На функцию 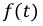 накладываются определенные ограничения и это объясняется тем, что интеграл (8.20) несобственный и значит необходимо решить вопрос о сходимости. Эти условия таковы:
накладываются определенные ограничения и это объясняется тем, что интеграл (8.20) несобственный и значит необходимо решить вопрос о сходимости. Эти условия таковы:
1) функция 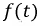 должна удовлетворять условиям Дирихле;
должна удовлетворять условиям Дирихле;
2) функция 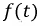 может возрастать во времени, но темп ее роста не должен превышать темпа убывания экспоненты.
может возрастать во времени, но темп ее роста не должен превышать темпа убывания экспоненты.
Для практически всех функций, которые рассматриваются в теории цепей, эти изображения известны.
Запишем наиболее значимые с практической точки зрения изображения типовых функций, используемых при расчете переходных процессов.
Изображение единичной функции:

Изображение константы:

Изображение экспоненты:

где 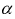 - любое комплексное число, в том числе и мнимое:
- любое комплексное число, в том числе и мнимое:

Изображение синусоиды:
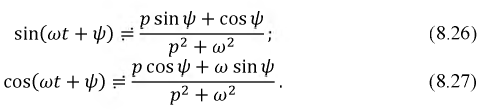
Изображение линейной функции:

Изображение производной:
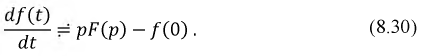
Изображение интеграла:

В качестве примера найдем изображения напряжений на индуктивности и емкости:
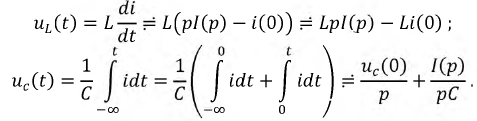
Первый интеграл в выражении для 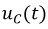 представляет собой напряжение на конденсаторе к моменту коммутации, то есть
представляет собой напряжение на конденсаторе к моменту коммутации, то есть 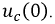 Ему соответствует изображение константы (8.22), поэтому:
Ему соответствует изображение константы (8.22), поэтому:
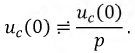
Закон Ома в операторной форме
На рис. 8.28 показано переключение контура с параметрами 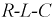 от источника
от источника 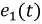 к источнику
к источнику 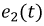
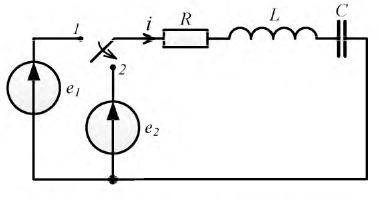
Рис. 8.28. Коммутации в схеме второго порядка
Для цепи рис. 8.28 после коммутации уравнение электрического равновесия относительно мгновенных значений токов и напряжений примет вид:
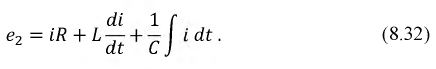
Будем полагать, что в схеме рис. 8.28 независимые начальные условия были не нулевыми.
Тогда уравнение (8.32) в операторной форме примет вид:
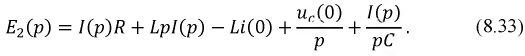
Решив уравнение (8.33) относительно тока 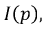 получим:
получим:
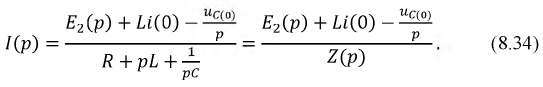
Формула (8.34) - закон Ома в операторной форме.
Входящее в нее выражение
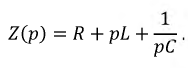
полностью повторяет комплексное сопротивление данной цепи в установившемся режиме при синусоидальном токе, если заменить оператор 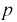 на
на 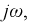 и носит название операторного сопротивления цепи. В составе числителя полученного уравнения появилось два новых слагаемых:
и носит название операторного сопротивления цепи. В составе числителя полученного уравнения появилось два новых слагаемых: 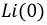 и
и 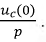 Это так называемые операторные или внутренние источники энергии, которые с физической точки зрения характеризуют энергию, запасенную в электрических и магнитных полях к моменту коммутации. При нулевых начальных условиях эти слагаемые отсутствуют и уравнение (8.34) при этом упростится. Полученное выражение позволяет составить так называемую послекоммутационную операторную схему цепи (рис. 8.29).
Это так называемые операторные или внутренние источники энергии, которые с физической точки зрения характеризуют энергию, запасенную в электрических и магнитных полях к моменту коммутации. При нулевых начальных условиях эти слагаемые отсутствуют и уравнение (8.34) при этом упростится. Полученное выражение позволяет составить так называемую послекоммутационную операторную схему цепи (рис. 8.29).
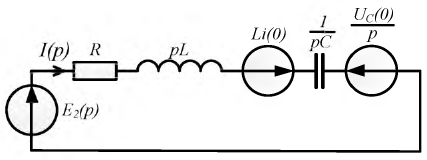
Рис. 8.29. Операторное изображение цепи по рис. 8.28 при ненулевых начальных условиях
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа:

Второй закон Кирхгофа:
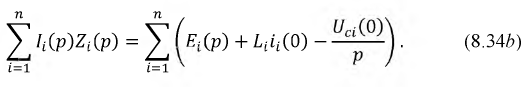
При нулевых начальных условиях (8.34b) упрощается.
Теорема разложения
Используя преобразования Лапласа, можно произвести расчет цепи в переходном процессе и получить при этом изображение соответствующего тока, напряжения и т.д. Однако искомой является временная функция соответствующего параметра, поэтому следующим этапом расчета должен быть переход от изображения к оригиналу. Это становится возможным, если воспользоваться обратным преобразованием Лапласа. Таблицу оригиналов и изображений по Лапласу для ряда функций можно найти в справочной литературе. Так как табличный ряд функций ограничен, то для перехода к оригиналу при расчете любой схемы целесообразно использовать общую методику с использованием формулы разложения. Любое решение в операторной форме может быть представлено в виде отношения двух полиномов, например, изображение тока:
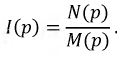
При этом дробь должна быть несократимой, степень полинома числителя меньше или равна степени полинома знаменателя, и он не должен иметь кратных корней, тогда:
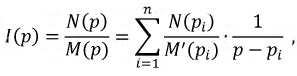
где 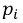 - корни уравнения
- корни уравнения 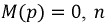 - общее число корней многочлена знаменателя.
- общее число корней многочлена знаменателя.
Тогда искомая формула разложения примет вид:
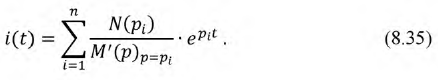
В результате решения уравнения 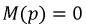 может получиться нулевой корень (при наличии в цепи постоянных источников ЭДС), его присутствие будет означать, что после коммутации в цепи будет некоторый установившийся режим, т.е. принужденная составляющая отлична от нуля. В случае, когда корни уравнения комплексно сопряженные, т.е. когда в цепи переходный процесс имеет колебательный характер, использование формулы разложения приводит к дополнительной особенности, заключающейся в том, что суммирование решений по двум комплексно-сопряженным корням предполагает устранение мнимой составляющей и удвоения ее вещественной части.
может получиться нулевой корень (при наличии в цепи постоянных источников ЭДС), его присутствие будет означать, что после коммутации в цепи будет некоторый установившийся режим, т.е. принужденная составляющая отлична от нуля. В случае, когда корни уравнения комплексно сопряженные, т.е. когда в цепи переходный процесс имеет колебательный характер, использование формулы разложения приводит к дополнительной особенности, заключающейся в том, что суммирование решений по двум комплексно-сопряженным корням предполагает устранение мнимой составляющей и удвоения ее вещественной части.
Методика расчета переходных процессов операторным методом
Последовательность расчета переходных процессов операторным методом заключается в выполнении следующих операций:
- Рассчитываются независимые начальные условия.
- Для цепи после коммутации составляется операторная схема, при этом ненулевые независимые начальные условия учитываются в виде операторных источников ЭДС.
- Любым из известных методов расчета электрических цепей составляется система уравнений относительно операторных изображений токов и напряжений.
- Решают полученную систему относительно искомых операторных токов и напряжений.
- Используя формулу разложения, определяют оригиналы искомых функций токов, напряжений и т. д.
Пример расчета переходных процессов операторным методом
Рассмотрим цепь, представленную на рис. 8.27 с теми же исходными данными.
1. Рассчитаем независимые начальные условия:
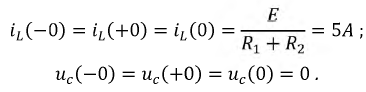
2. Составляем операторную схему.
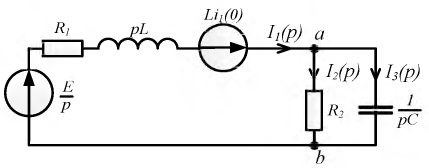
Рис. 8.30. Операторная схема
3. Составляем систему уравнений для расчета изображений токов и напряжений:
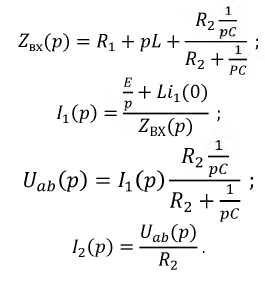
 Расчет представленной выше системы уравнений при условии
Расчет представленной выше системы уравнений при условии 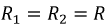 для тока
для тока 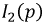 имеет вид:
имеет вид:
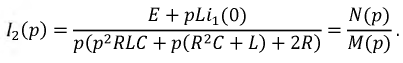
5. Используя формулу разложения, найдем оригинал 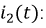
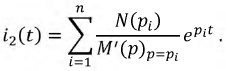
Приравняв полином знаменателя к нулю 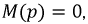 найдем его корни
найдем его корни
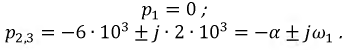
Запишем производную от многочлена знаменателя в виде:
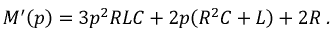
Оригинал функции:
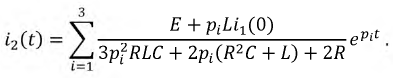
Последовательно подставляя значения каждого из корней, определяем составляющие тока:
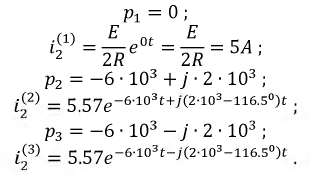
Суммируя выражения для каждого из комплексно сопряженных корней, получим удвоение вещественной части тока 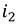 и сокращение его мнимых частей, в итоге такого преобразования получим окончательное решение задачи:
и сокращение его мнимых частей, в итоге такого преобразования получим окончательное решение задачи:
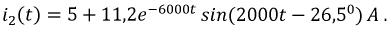
Данный результат полностью совпадает с выражением для 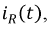 которое было получено ранее классическим методом.
которое было получено ранее классическим методом.
Особенности расчета переходных процессов в цепях с взаимной индуктивностью
На рис. 8.31 представлена схема двух индуктивно связанных катушек.
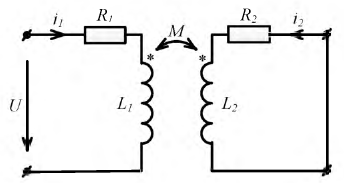
Рис. 8.31. Индуктивно связанные катушки в режиме короткого замыкания
Пусть и параметры катушек соответственно 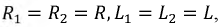 цепь подключается к источнику постоянного напряжения и сопротивление нагрузки равно нулю
цепь подключается к источнику постоянного напряжения и сопротивление нагрузки равно нулю 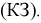 Поставим задачу определения токов
Поставим задачу определения токов 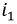 и
и 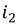 в переходном процессе. Для первой и второй катушек запишем уравнения по второму закону Кирхгофа, причем направления обхода контуров зададим совпадающими с направлениями токов
в переходном процессе. Для первой и второй катушек запишем уравнения по второму закону Кирхгофа, причем направления обхода контуров зададим совпадающими с направлениями токов 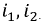 Учитывая, что
Учитывая, что 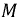 - взаимная индуктивность катушек, получим систему:
- взаимная индуктивность катушек, получим систему:
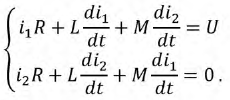
Решение данной системы проведем операторным методом. Считая, что начальные условия нулевые, перепишем уравнения в операторной форме:
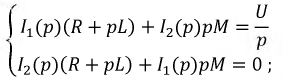
где 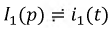 и
и 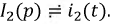
Операторные изображения токов первой и второй катушек:
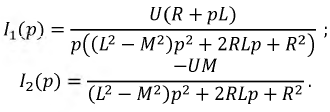
Корни многочлена знаменателя:
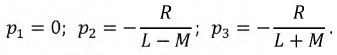
Используя формулу разложения, найдем оригиналы функций токов:
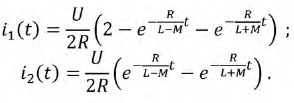
Из анализа полученных уравнений следует, что в случае, когда или 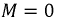 (отсутствует индуктивная связь), или
(отсутствует индуктивная связь), или 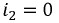 (режим холостого хода), выражения для токов упрощаются:
(режим холостого хода), выражения для токов упрощаются:
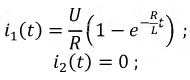
то есть вторая катушка не участвует в рассматриваемом процессе.
Для тока 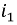 перечисленные выше ситуации соответствуют подключению цепи
перечисленные выше ситуации соответствуют подключению цепи 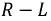 к источнику постоянного напряжения, которое мы получили раньше. Построим картину переходного процесса (рис. 8.32). Для наглядности функцию тока
к источнику постоянного напряжения, которое мы получили раньше. Построим картину переходного процесса (рис. 8.32). Для наглядности функцию тока 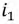 построим как при наличии, так и при отсутствии взаимной индуктивности.
построим как при наличии, так и при отсутствии взаимной индуктивности.
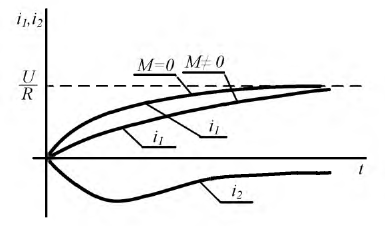
Рис. 8.32. Графики токов 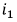 и
и 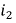 в переходном процессе для индуктивно связанных катушек
в переходном процессе для индуктивно связанных катушек
Наличие магнитной связи 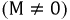 привело к увеличению порядка характеристического уравнения и появлению в токе
привело к увеличению порядка характеристического уравнения и появлению в токе 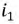 составляющей с большей постоянной времени, чем при
составляющей с большей постоянной времени, чем при 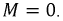 Это привело к замедлению роста тока в первой катушке. Причину такого изменения тока
Это привело к замедлению роста тока в первой катушке. Причину такого изменения тока 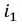 можно объяснить и тем, что ток
можно объяснить и тем, что ток 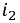 препятствует изменению тока
препятствует изменению тока 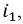 увеличивая тем самым постоянную времени первой катушки.
увеличивая тем самым постоянную времени первой катушки.
График тока 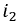 показывает, что в установившемся режиме ток в цепи второй катушки отсутствует, несмотря на режим короткого замыкания.
показывает, что в установившемся режиме ток в цепи второй катушки отсутствует, несмотря на режим короткого замыкания.
Методика расчета переходного процесса с помощью интеграла Дюамеля
Рассмотрим особенности переходного процесса при действии на цепь источника напряжения произвольной формы. Это определяет свои особенности расчета, на которых остановимся подробнее.
Пусть на вход некоторого пассивного двухполюсника (рис. 8.33,а) подано напряжение произвольной формы.
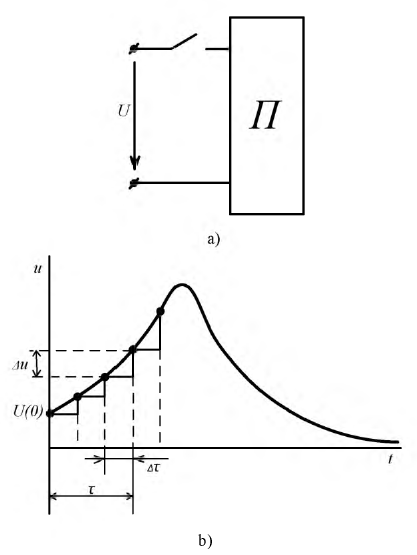
Рис. 8.33.Пассивный двухполюсник (а) и сигнал на входе двухполюсника (b).
Пусть 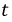 - это момент времени, в который необходимо найти значение тока в переходном процессе. Входное напряжение
- это момент времени, в который необходимо найти значение тока в переходном процессе. Входное напряжение 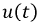 задано графически (рис. 8.33,b). Аппроксимируем его характеристику вписанной в нее ступенчатой кривой. Из графика входного напряжения следует, что в момент коммутации напряжение скачком увеличится от 0 до
задано графически (рис. 8.33,b). Аппроксимируем его характеристику вписанной в нее ступенчатой кривой. Из графика входного напряжения следует, что в момент коммутации напряжение скачком увеличится от 0 до 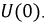 Каждый следующий скачок напряжения величиной
Каждый следующий скачок напряжения величиной 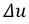 возникает со смещением во времени на
возникает со смещением во времени на 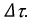 Любой произвольно выбранный скачок напряжения
Любой произвольно выбранный скачок напряжения 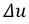 наблюдается в момент времени
наблюдается в момент времени 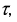 где
где 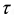 это время, отсчитываемое от момента возникновения входного напряжения. Аналитически входное напряжение может быть описано приближенным выражением:
это время, отсчитываемое от момента возникновения входного напряжения. Аналитически входное напряжение может быть описано приближенным выражением:
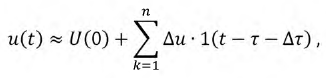
где 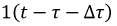 —единичная функция со смещением относительно времени наблюдения
—единичная функция со смещением относительно времени наблюдения 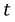 на
на 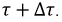
Начальный скачок напряжения 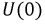 вызовет ток в двухполюснике, который равен:
вызовет ток в двухполюснике, который равен:
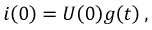
где 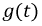 носит название переходной проводимости.
носит название переходной проводимости.
Пусть 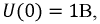 тогда
тогда 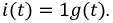 Функция
Функция 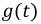 численно равна функции тока в двухполюснике, при условии, что он подключается к источнику постоянного напряжения величиной 1В. Таким образом, для определения
численно равна функции тока в двухполюснике, при условии, что он подключается к источнику постоянного напряжения величиной 1В. Таким образом, для определения 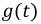 необходимо найти
необходимо найти 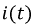 любым из известных методов расчета переходных процессов (классическим, операторным) при
любым из известных методов расчета переходных процессов (классическим, операторным) при 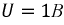 и впредь будем считать ее известной. Так как в переходных режимах рассчитывают как токи, так и напряжения, то при расчете напряжения на каком-либо участке цепи необходимо предварительно рассчитать переходную функцию
и впредь будем считать ее известной. Так как в переходных режимах рассчитывают как токи, так и напряжения, то при расчете напряжения на каком-либо участке цепи необходимо предварительно рассчитать переходную функцию 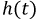 численно равную
численно равную 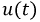 при условии, что входное напряжение постоянное и численно равно IB. Ток, вызванный любым скачком напряжения, равен:
при условии, что входное напряжение постоянное и численно равно IB. Ток, вызванный любым скачком напряжения, равен:
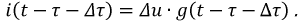
Тогда ток, вызванный действием входного напряжения, определится по выражению:
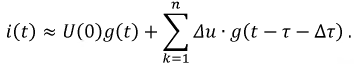
Умножим 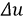 на
на 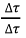 и устремим
и устремим 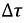 к нулю. Тогда
к нулю. Тогда 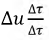 заменится в пределе на
заменится в пределе на 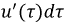 и выражение для тока можно заменить точным, а именно:
и выражение для тока можно заменить точным, а именно:
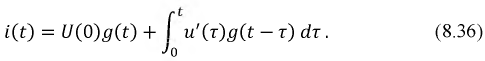
Формула 8.36 представляет собой одну из форм записи интеграла Дюамеля. Данная форма записи соответствует непрерывной функции подводимого напряжения. Однако в ряде случаев форма входного напряжения может быть представлена кусочно-непрерывной функцией, имеющей точки разрыва первого рода. Это привносит свою специфику при использовании интеграла Дюамеля.
Представленный на рис. 8.34 график показывает, что общее время существования функции 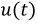 представлено тремя интервалами
представлено тремя интервалами 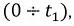
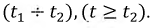 На каждом из интервалов действует разное напряжение и поэтому решение для тока на каждом временном интервале надо находить отдельно.
На каждом из интервалов действует разное напряжение и поэтому решение для тока на каждом временном интервале надо находить отдельно.
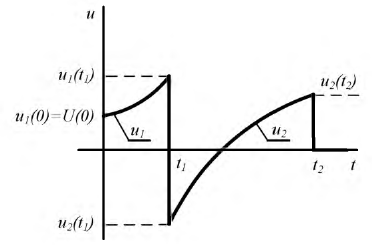
Рис. 8.34. Графическое изображение напряжения на входе двухполюсника
1. 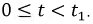 Предполагается, что переходная проводимость
Предполагается, что переходная проводимость 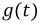 известна. Тогда ток на первом интервале равен:
известна. Тогда ток на первом интервале равен:
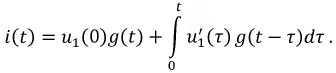
Верхний предел интеграла открыт, поскольку в результате решения мы должны получить функцию тока, т.е. иметь возможность определить его в любой момент времени в интервале 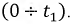
2. 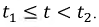 Переходный процесс на первом временном интервале не закончился, а на входе цепи появилось новое напряжение, вызывающее новый переходный процесс, таким образом, на втором временном интервале действуют накладывающиеся друг на друга два переходных процесса:
Переходный процесс на первом временном интервале не закончился, а на входе цепи появилось новое напряжение, вызывающее новый переходный процесс, таким образом, на втором временном интервале действуют накладывающиеся друг на друга два переходных процесса:
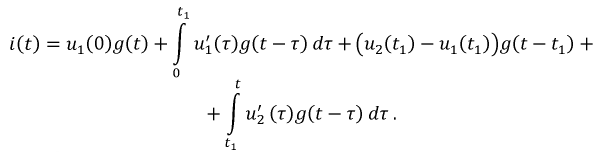
3. 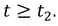 Аналогичные рассуждения можно провести и для третьего интервала:
Аналогичные рассуждения можно провести и для третьего интервала:
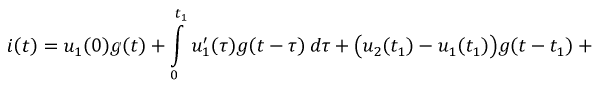
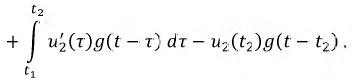
В общем случае решения на смежных интервалах должны совпадать, однако это бывает далеко не всегда, т.к. токи и падения напряжения, например, на резисторах могут изменяться скачком.
Проверка осуществляется:
- 1) на участках сопряжения.
- 2) в момент коммутации при
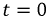 (только для первого решения) и при
(только для первого решения) и при 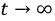 (для последнего решения).
(для последнего решения).
Пример расчета переходного процесса с помощью интеграла Дюамеля
Последовательность расчета переходных процессов с помощью интеграла Дюамеля включает четыре этапа:
- Любым из известных методов определяют переходную проводимость
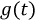 или переходную функцию
или переходную функцию 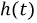
- Производят замену аргументов
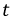 на
на 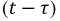 и получают соответственно функции
и получают соответственно функции 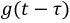 или
или 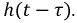
- По заданной функции входного напряжения определяют ее производную по
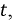 а затем производят замену
а затем производят замену 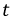 на
на 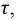 т.е., получают
т.е., получают 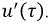
- Параметры, найденные в пунктах 1-3, подставляют в формулу интеграла Дюамеля и определяют итоговую функцию
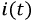 или
или 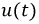 в переходном процессе.
в переходном процессе.
Рассмотрим пример.
Пусть дана схема (рис. 8.35,а), на входе которой действует напряжение 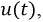 (рис. 8.35,b).
(рис. 8.35,b).
Определить 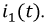 Исходные параметры схемы:
Исходные параметры схемы:
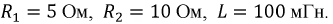
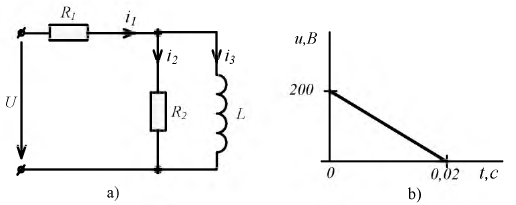
Рис. 8.35.Схема пассивного двухполюсника (а) и график входного напряжения (b)
Определим переходную проводимость, используя классический метод:
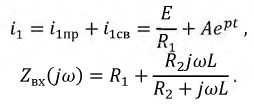
Осуществляя замену 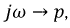 получим характеристическое уравнение:
получим характеристическое уравнение:
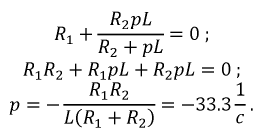
При 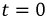 получим:
получим:
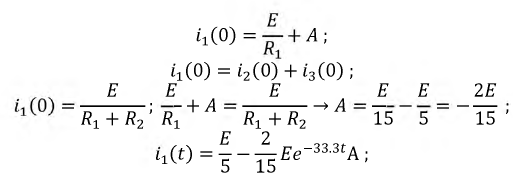
При 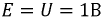 получим:
получим:
Заменяем переменную 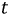 на
на 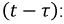
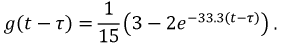
Определим производную от напряжения:
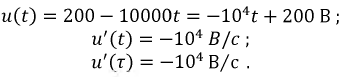
Общее решение сложится из решений для двух интервалов.
Первый интервал 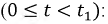
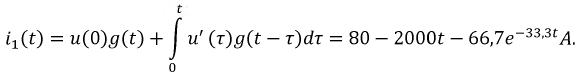
Проверку производим по двум направлениям.
Качественная.
В решении присутствуют слагаемые, повторяющие форму подводимого напряжения и свободная составляющая.
Количественная.
При 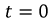 получим:
получим:
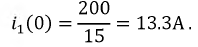
Этот результат соответствует параметрам цепи.
Второй интервал 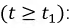
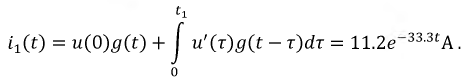
Вновь выполним качественную и количественную проверку полученного решения.
Качественная.
Так как действие входного источника энергии закончилось, то решение должно содержать только свободную составляющую, что и подтверждается полученным результатом.
Количественная.
При 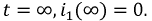
Последний этап проверки выполним для момента времени 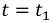 поскольку он принадлежит обоим интервалам. И в том и в другом случаях решения совпадают:
поскольку он принадлежит обоим интервалам. И в том и в другом случаях решения совпадают:
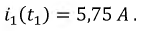
Частотный метод расчета переходных процессов
Этот метод базируется на известном преобразовании Фурье.
Интеграл Фурье
Периодическая несинусоидальная функция может быть разложена в дискретный ряд Фурье:
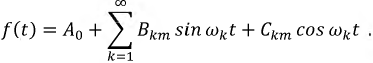
Входящие в него коэффициенты 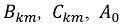 являются функциями времени и для их определения введем дополнительную переменную
являются функциями времени и для их определения введем дополнительную переменную 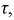 тогда:
тогда:
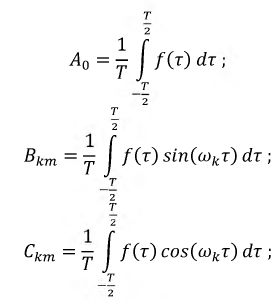
где 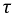 — переменная в интервале
— переменная в интервале 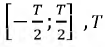 - период несинусоидальнои функции или первой гармоники.
- период несинусоидальнои функции или первой гармоники.
Поскольку ряд дискретный, то между двумя соседними частотами всегда имеется интервал:
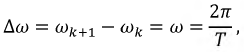
где 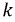 - номер гармоники.
- номер гармоники.
Подставив коэффициенты в дискретный ряд Фурье, получим:
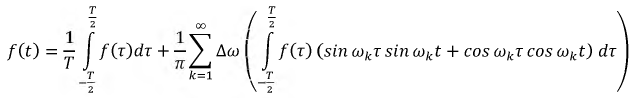
Свернём подынтегральное выражение в скобках и получим следующую формулу:
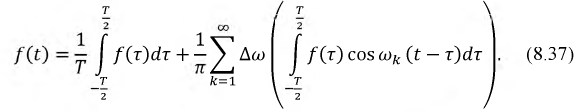
При неограниченном увеличении периода, т.е. при 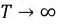 перейдем от периодической функции к непериодической.
перейдем от периодической функции к непериодической.
Тогда частотный интервал 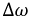 стремится к
стремится к 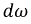 и поэтому знак суммы заменим на интеграл. При этом исходное уравнение упростится и примет следующий вид:
и поэтому знак суммы заменим на интеграл. При этом исходное уравнение упростится и примет следующий вид:
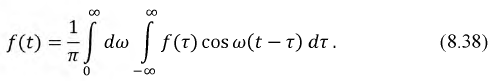
Полученное выражение (8.38) представляет собой интеграл Фурье в тригонометрической форме.
Таким образом, осуществлен переход от периодической функции с дискретным спектром частот к непериодической функции с непрерывным частотным спектром. Внутренний интеграл представляет собой сумму бесконечного числа гармоник с бесконечно малыми амплитудами.
Преобразование Фурье
Для получения искомого преобразования перепишем полученное выражение интеграла Фурье (8.38), формально введя отрицательные частоты, следующим образом:
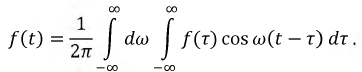
Отрицательные частоты не имеют физического смысла, однако, позволяют сделать запись в более симметричной форме. Прибавим к полученной функции мнимый ноль 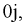 который в свою очередь зададим выражением:
который в свою очередь зададим выражением:
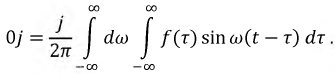
Воспользуемся формулой Эйлера для записи функции в показательном виде:
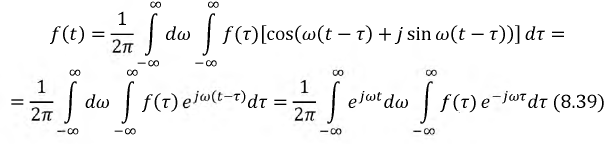
Отдельно выделим внутренний интеграл в (8.39) и произведем в нем замену 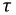 на
на 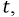 т.к. в обоих интегралах разные переменные, что позволит получить выражение:
т.к. в обоих интегралах разные переменные, что позволит получить выражение:
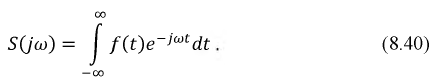
Полученный интеграл (8.40) носит название прямого преобразования Фурье и является частотным спектром (спектральной плотностью) периодической функции 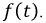
Прямое преобразование Фурье есть функция комплексная и поэтому может быть представлена в виде:
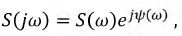
где 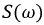 - амплитудно-частотная характеристика (АЧХ),
- амплитудно-частотная характеристика (АЧХ), 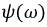 - фазочастотная характеристика (ФЧХ).
- фазочастотная характеристика (ФЧХ).
Подставив (8.40) в (8.39), получим еще одно соотношение:
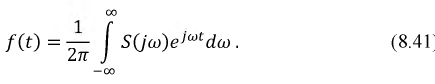
Интеграл по формуле (8.41) представляет собой обратное преобразование Фурье, позволяющее по известному частотному спектру определить временную зависимость сигнала.
Сравним прямое преобразование Фурье и интеграл Лапласа.
Если в прямом преобразовании Фурье заменить 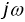 на
на 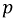 и учесть, что
и учесть, что 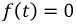 при
при 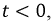 получим:
получим:
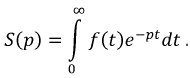
Следовательно, преобразование Фурье можно использовать в расчетах переходных процессов. Полученное равенство показывает, что преобразование Лапласа является более «мощным», чем преобразование Фурье, так как оператор 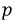 - может быть любым (вещественным, комплексным, мнимым), в то время как
- может быть любым (вещественным, комплексным, мнимым), в то время как 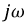 - чисто мнимое число. Из вышесказанного следует, что, если для некоторой функции известно изображение по Лапласу, то для получения частотного спектра достаточно
- чисто мнимое число. Из вышесказанного следует, что, если для некоторой функции известно изображение по Лапласу, то для получения частотного спектра достаточно 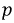 заменить на
заменить на 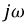 в этом выражении и выделить его АЧХ и ФЧХ.
в этом выражении и выделить его АЧХ и ФЧХ.
Законы Ома и Кирхгофа для частотных спектров
Для схемы рис. 8.29 ранее был записан закон Ома в операторной форме (8.34). Для получения частотного спектра необходимо оператор 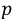 заменить на
заменить на 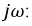
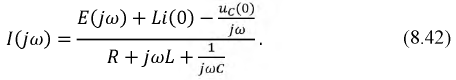
Аналогичные преобразования проведем и в выражениях для законов Кирхгофа в операторной форме
Первый закон Кирхгофа (8.34а) в частотной форме:
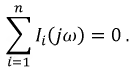
Второй закон Кирхгофа (8.34b) в частотной форме:
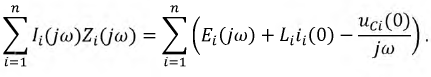
Пример расчета спектральной плотности сигнала
Пусть на вход некоторого двухполюсника подается единичный импульс напряжения длиной 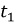 (рис. 8.36).
(рис. 8.36).
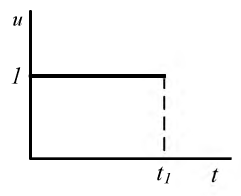
Рис. 8.36. График импульса напряжения прямоугольной формы
Определим частотный спектр этого импульса. Так как площадь импульса конечна, то преобразование может быть получено в следующем виде:
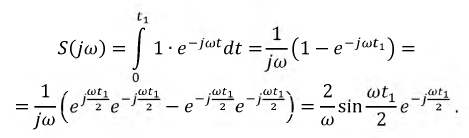
Из полученного выражения для спектральной плотности рассматриваемой функции выделим и построим АЧХ и ФЧХ:
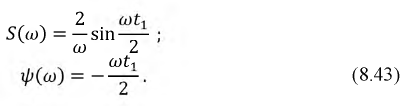
АЧХ представляет собой функцию выпрямленной синусоиды, амплитуда которой убывает по экспоненциальному закону (рис. 8.37).
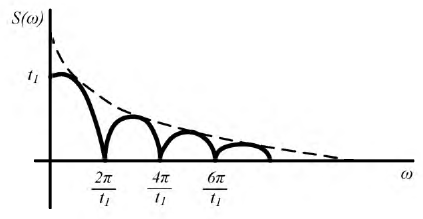
Рис. 8.37. АЧХ единичного импульса длительностью 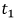
Аналогичного рода рассуждения позволяют построить ФЧХ функции (рис. 8.38).
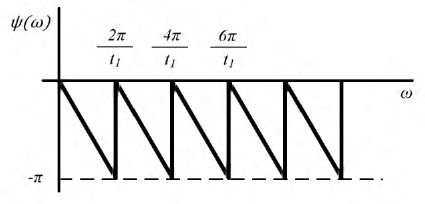
Рис. 8.38. ФЧХ единичного импульса длительностью 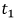
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
- Переходные процессы