
Разложение многочленов на множители с примерами решения
Содержание:
Разложение многочленов на множители
Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:
- вынесении общего множителя за скобки;
- способе группировки;
- формулах сокращённого умножения;
- применении разных способов разложения многочленов на множители.
Вынесение общего множителя за скобки
Вы уже умеете раскладывать на множители натуральные числа. Например,
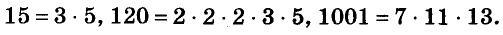
На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен 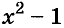
Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.
Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 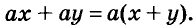 Это означает, что данный многочлен ах + ау разложен на два множителя:
Это означает, что данный многочлен ах + ау разложен на два множителя: 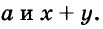
Другие примеры:
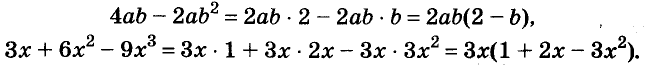
Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.
Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 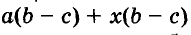 общий множитель b - с. Его также можно выносить за скобки:
общий множитель b - с. Его также можно выносить за скобки:
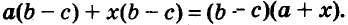
Один и тот же многочлен можно разложить на множители по-разному. Например,
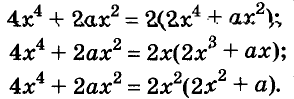
Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.
Пусть, например, надо найти значение выражения 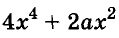 при условии, когда
при условии, когда 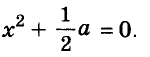
Чтобы использовать условие, это упражнение можно решить так:
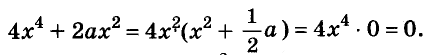
Здесь вынесено за скобки не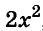 , а
, а 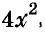 тогда в скобках имеем выражение, значение которого известно из условия.
тогда в скобках имеем выражение, значение которого известно из условия.
Пример:
Разложите на множители многочлен 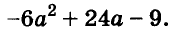
Решение:
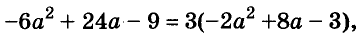 или
или 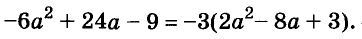
Пример:
Разложите на множители многочлен
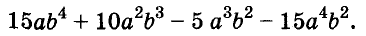
Решение:
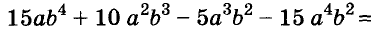
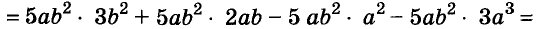
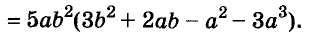
Пример:
Докажите, что число 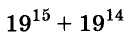 делится на 20.
делится на 20.
Доказательство:
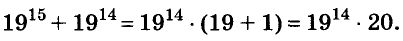 Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.
Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.
Пример:
Решите уравнение 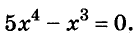
Решение:
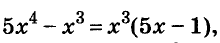 поэтому данное уравнение равносильно уравнению
поэтому данное уравнение равносильно уравнению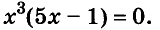 Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.
Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.
Значит, 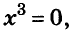 отсюда х = 0, или 5х - 1 = 0, отсюда х = 0,2.
отсюда х = 0, или 5х - 1 = 0, отсюда х = 0,2.
Ответ. Уравнение имеет два корня: 0 и 0,2.
Способ группировки
Разложим на множители многочлен 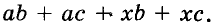 Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель
Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель 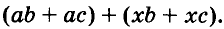 Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение
Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение 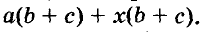 Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение
Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение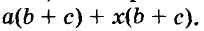
Указанные преобразования можно записать цепочкой:
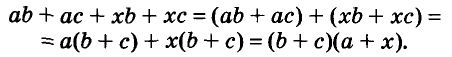
Такой способ разложения многочленов на множители называют способом группировки.
Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:
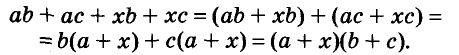
Получили такой же результат.
Разложим на множители многочлен 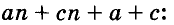
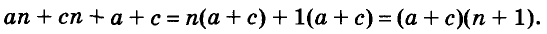
Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.
Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 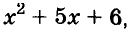 • запишем одночлен
• запишем одночлен 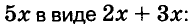
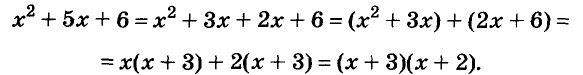
Подобные преобразования также можно выполнять, используя тождества.
Пример:
Разложите на множители многочлен:
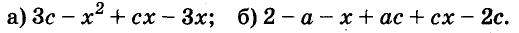
Решение:
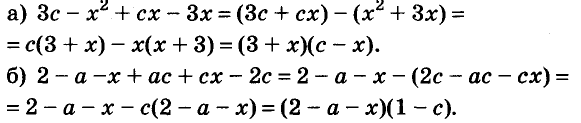
Ответ. 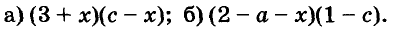
Пример:
Решите уравнение: 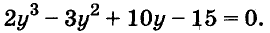
Решение:
Разложим левую часть уравнения на множители:
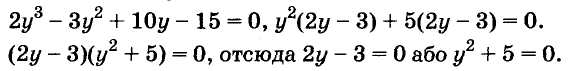
Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как 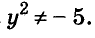
Ответ. у = 1,5.
Квадрат двучлена
Решая различные задачи, часто приходится умножать двучлены вида 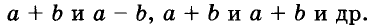 Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.
Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.
Умножим двучлен 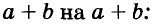
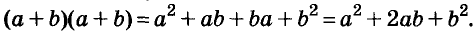 Следовательно,
Следовательно,
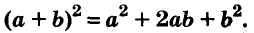
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.
Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:
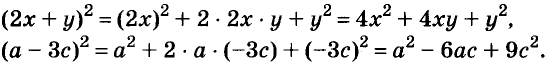
Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:
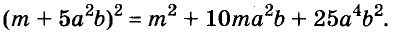
По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе 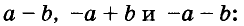
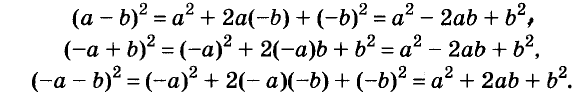
Запомните формулу
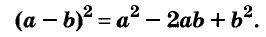
Формулы квадрата двучлена используют и в «обратном направлении»:
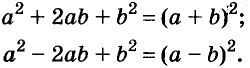
Формулу 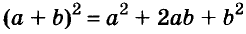 часто называют формулой квадрата суммы двух выражений,
часто называют формулой квадрата суммы двух выражений, 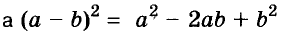 — квадрата разности двух выражений.
— квадрата разности двух выражений.
Для положительных чисел а и b формулу
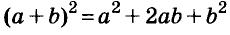 можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов
можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов 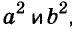 а также прямоугольников ab и ab.
а также прямоугольников ab и ab.
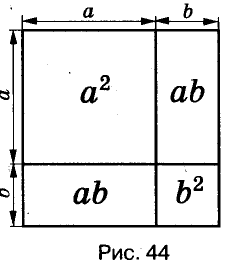
Существуют и другие формулы сокращённого умножения:
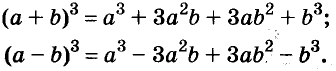
Пример:
Возведите в квадрат двучлен 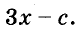
Решение:
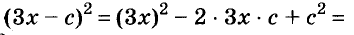
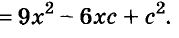
Пример:
Упростите выражение 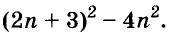
Решение:
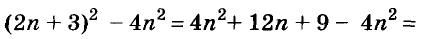
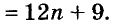
Пример:
Представьте в виде многочлена выражение:
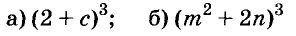
Решение:
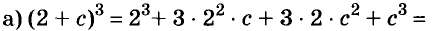
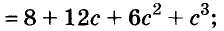
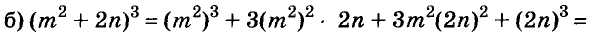
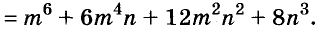
Пример:
Представьте выражение в виде степени двучлена:
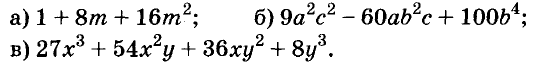
Решение:
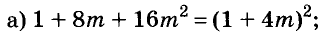
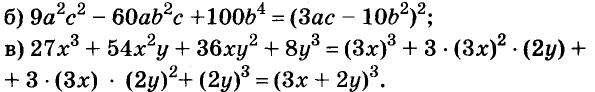
Разность квадратов
Умножим сумму переменных а и b на их разность.
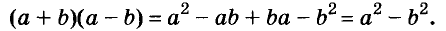
Значит, 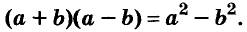
Это равенство — тождество. Словами его читают так:
Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.
Пользуясь доказанной формулой, можно сразу записать:
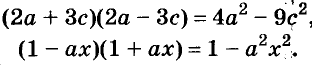
Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:
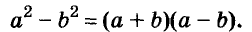
Разность квадратов двух выражений равна произведению их суммы и разности.
Пример:
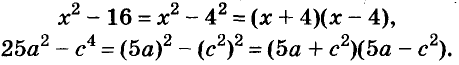
Формула разности квадратов очень удобна для разложения многочленов на множители.
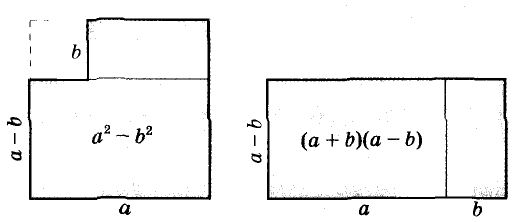
Для положительных чисел а и b формулу 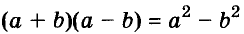 можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.
можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.
Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.
Пример:
Напишите разность квадратов и квадрат разности выражений 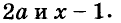
Решение:
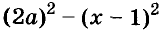 — разность квадратов;
— разность квадратов; 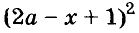 — квадрат разности данных выражений.
— квадрат разности данных выражений.
Пример:
Запишите в виде произведения двух двучленов выражение:
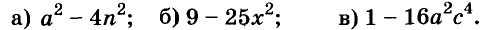
Решение:
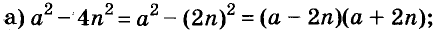
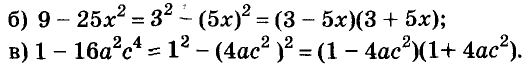
Пример:
Представьте в виде двучлена выражение:

Решение:
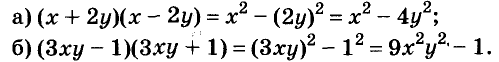 .
.
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.
Использование формул сокращённого умножения
С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 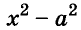 можно представить в виде произведения по формуле разности квадратов:
можно представить в виде произведения по формуле разности квадратов:
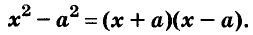
Примеры:
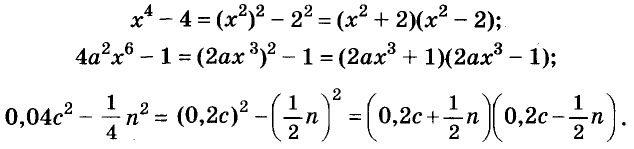
Трёхчлены 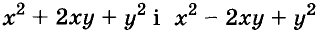 раскладывают на множители по формуле квадрата двучлена:
раскладывают на множители по формуле квадрата двучлена:
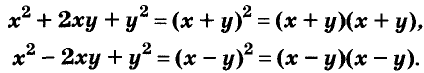
Примеры:
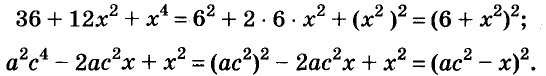
Полученные, выражения можно разложить на множители и записать так: 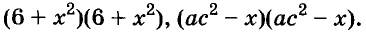
Многочлен 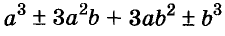 можно разложить на множители по формуле куба двучлена:
можно разложить на множители по формуле куба двучлена:
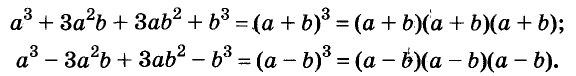
Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.
Например, 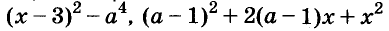 — не многочлены, но и их можно представить в виде произведений многочленов:
— не многочлены, но и их можно представить в виде произведений многочленов:
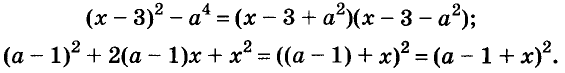
Пример:
Разложите на множители многочлен:
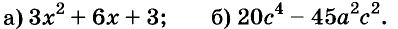
Решение:
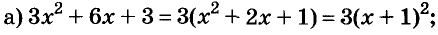
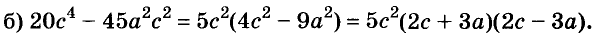
Пример:
Решите уравнение 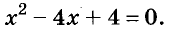
Решение:
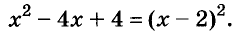
Значит, данное уравнение равносильно такому:
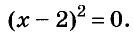
Квадрат числа равен нулю только тогда, когда это число равно 0. А х - 2 = 0, когда х = 2.
Ответ. х = 2.
Пример:
Разложите на множители многочлен:
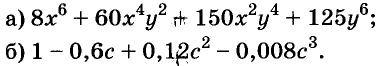
Решение:
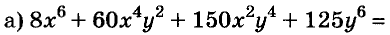
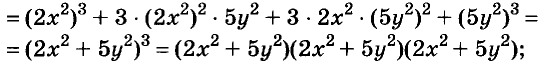
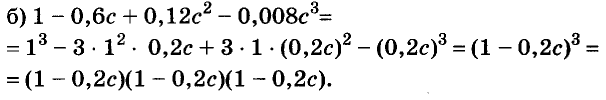
Разность и сумма кубов
Выполним умножение многочленов 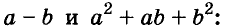
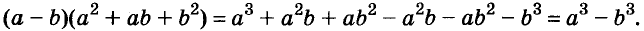
Следовательно, при любых значениях а и b
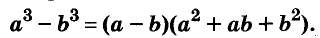
Трёхчлен 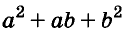 называют неполным квадратом суммы выражений а и b (от
называют неполным квадратом суммы выражений а и b (от 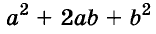 он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:
он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:
разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Выполним умножение многочленов 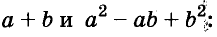
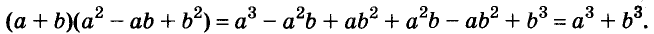
Следовательно,
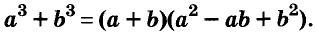
Трёхчлен 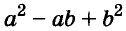 называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:
называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:
сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.
Примеры:
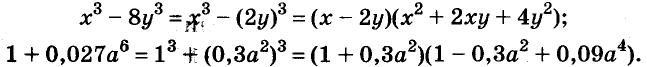
Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.
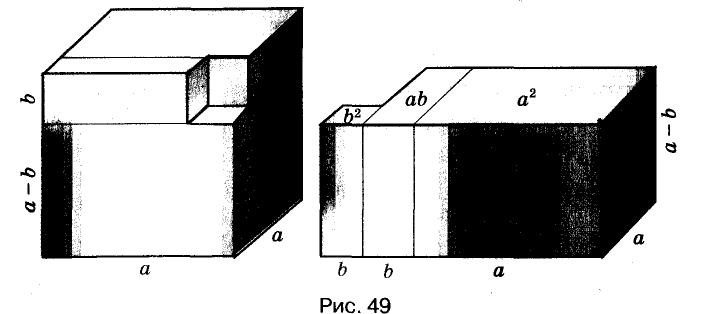 Если умножить на а - b выражения
Если умножить на а - b выражения 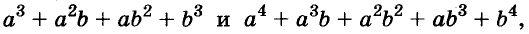 то получим формулы:
то получим формулы:
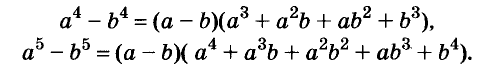
Можно доказать, что для каждого натурального значения n истинна формула:
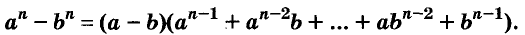
Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.
Пример:
Разложите на множители двучлен: 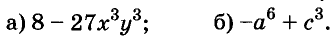
Решение:
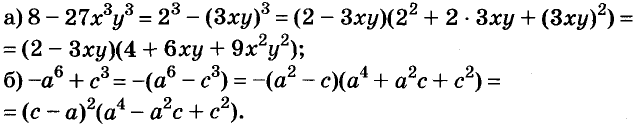
Пример:
Найдите произведение многочленов: 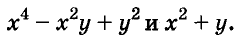 •
•
Решение:
Первый способ. По формуле суммы кубов: 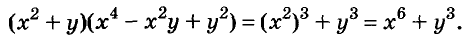
Второй способ. По правилу умножения многочленов:
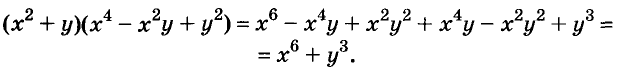
Применение разных способов разложения многочленов на множители
Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.
Пример:
Разложите на множители многочлен
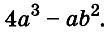
Решение:
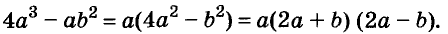
Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.
Пример:
Разложите на множители выражение
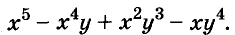
Решение:
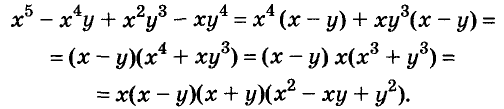
Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.
Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.
В этом случае можно использовать такое правило-ориентир:
- Вынести общий множитель (если он есть) за скобки.
- Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
- Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
- Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.
Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.
Пример:
Разложите на множители двучлен 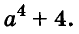
Решение:
Прибавим к данному двучлену выражение 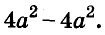
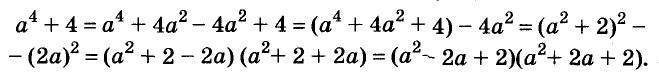
Пример:
Разложите на множители выражение 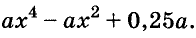
Решение:
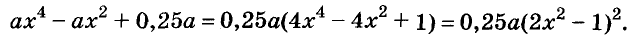
Пример:
Представьте многочлен 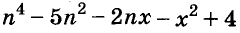 в виде разности квадратов двух многочленов.
в виде разности квадратов двух многочленов.
Решение:
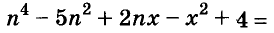
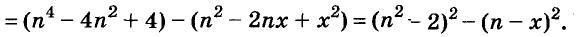
Пример:
Докажите, что число 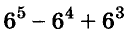 делится на 31.
делится на 31.
Доказательство:
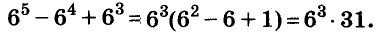
Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.
Исторические сведения:
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо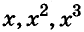 писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение
писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение 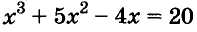 Ф. Виет записывал так:
Ф. Виет записывал так:
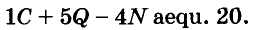
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать 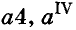 . Записи
. Записи 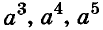 предложил Р. Декарт.
предложил Р. Декарт.
Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 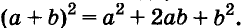 Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.
Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.
В учебнике рассмотрены простейшие формулы сокращённого умножения.
Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:
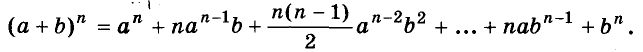
Напомню:
Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.
Простейшие способы разложения многочленов на множители:
- вынесение общего множителя за скобки;
- способ группировки;
- использование формул сокращённого умножения.
Примеры:
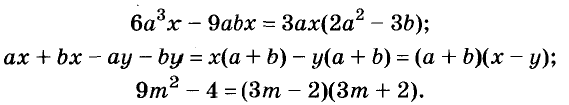
Формулы сокращённого умножения
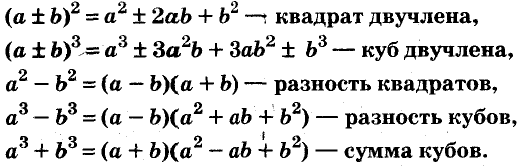
Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.
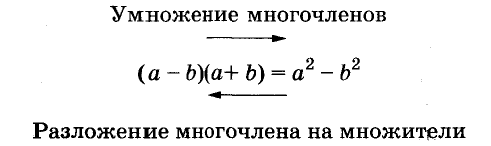
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |