Двумерная случайная величина (𝑋; 𝑌) имеет равномерное распределение плотности вероятности в треугольной области 𝐴𝐵𝐶, заданной функцией 𝑓(𝑥; 𝑦).

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16444
		Прошла проверку преподавателем МГУ
		245 руб.

Двумерная случайная величина (𝑋; 𝑌) имеет равномерное распределение плотности вероятности в треугольной области 𝐴𝐵𝐶, заданной функцией 𝑓(𝑥; 𝑦). Эта функция принимает значение 1/𝑆, если точка с координатами (𝑥; 𝑦) принадлежит области 𝐴𝐵𝐶, и 0, если точка с координатами (𝑥; 𝑦) не принадлежит данной области (𝑆 – площадь треугольника 𝐴𝐵𝐶 с вершинами в точках 𝐴{0; 1}, 𝐵{1; 1}, 𝐶{1; −1}). Определить плотности распределения составляющей 𝑋 – 𝑓𝑋 (𝑥) и составляющей 𝑌 – 𝑓𝑌 (𝑦), математические ожидания 𝑀𝑋 и 𝑀𝑌, дисперсии 𝐷𝑋 и 𝐷𝑌. Найти коэффициент корреляции случайных величин 𝑋 и 𝑌; установить, являются ли случайные величины независимыми.

Решение

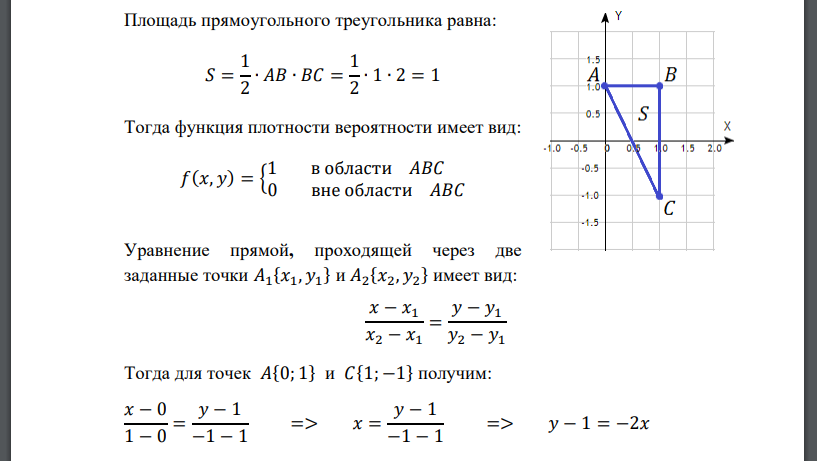
Площадь прямоугольного треугольника равна: Тогда функция плотности вероятности имеет вид:  в области 𝐴𝐵𝐶 0 вне области 𝐴𝐵𝐶 Уравнение прямой, проходящей через две заданные точки 𝐴1 {𝑥1, 𝑦1 } и 𝐴2 {𝑥2, 𝑦2 } имеет вид:  Тогда для точек 𝐴{0; 1} и 𝐶{1; −1} получим:  уравнение стороны 𝐴𝐶 Границы области 𝐴𝐵𝐶 запишем двумя способами:  Найдем плотности распределения составляющих 𝑋 и 𝑌 Найдем математическое ожидание  Дисперсия составляющей Найдем математическое ожидание  Дисперсия составляющей Найдем математическое ожидание 𝑀𝑋𝑌Найти коэффициент корреляции 𝑟𝑥𝑦 случайных величин 𝑋 и 𝑌:  Выясним, являются ли величины 𝑋 и 𝑌 зависимыми. Случайные величины 𝑋 и 𝑌 называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид