Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

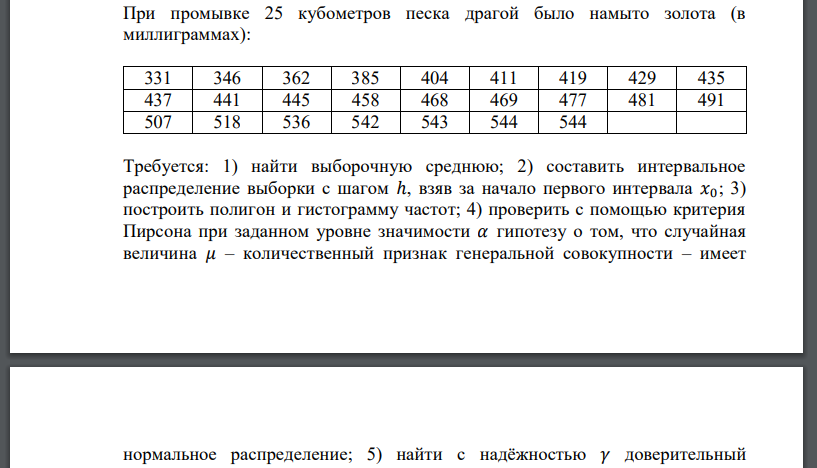
При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется

При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется Теория вероятностей
При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется Решение задачи
При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется
При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется Выполнен, номер заказа №16401
При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется Прошла проверку преподавателем МГУ
При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется  245 руб. 

При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется: 1) найти выборочную среднюю; 2) составить интервальное распределение выборки с шагом ℎ, взяв за начало первого интервала 𝑥0; 3) построить полигон и гистограмму частот; 4) проверить с помощью критерия Пирсона при заданном уровне значимости 𝛼 гипотезу о том, что случайная величина 𝜇 – количественный признак генеральной совокупности – имеет нормальное распределение; 5) найти с надёжностью 𝛾 доверительный интервал для оценки неизвестного математического ожидания признака 𝜇 генеральной совокупности. 𝛼 = 0,05; 𝛾 = 0,95; 𝜎 = 55; ℎ = 50; 𝑥0 = 325

Решение

1) Найдем выборочную среднюю.  2) Составим интервальное распределение выборки с шагом, взяв за начало первого интервала . Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Номер интервала Интервал Середина интервала Частота, 3) Построим полигон частот (синим) и гистограмму частот (черным). 4) Выборочная дисперсия:  Исправленная дисперсия:  Исправленное среднее квадратическое отклонение равно:  Вероятность попадания случайной величины в каждый интервал равна приращению функции распределения:  Теоретические частоты определим по формуле  и вычислим значения  Результаты запишем в таблицу Интервал  Получили . Число степеней свободы . По таблице при уровне значимости  находим Так как , то нет оснований отвергать гипотезу о нормальном распределении при заданном уровне значимости. 5) Доверительный интервал для математического ожидания a нормально распределенной случайной величины равен:  где  – значение, определяемое по таблице квантилей распределения Стьюдента в зависимости от числа степеней свободы  и доверительной вероятности  По таблице квантилей распределения Стьюдента находим:  и искомый доверительный интервал имеет вид:

При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется

При промывке 25 кубометров песка драгой было намыто золота (в миллиграммах): 331 346 362 385 404 411 419 429 435 437 441 445 458 468 469 477 481 491 507 518 536 542 543 544 544 Требуется