
Скалярное произведение и его свойства с примерами решения
Содержание:
Скалярное произведение и его свойства в векторной алгебре
Скалярное произведение векторов
Определение: Скалярным произведением двух векторов 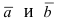
Пример:
Вычислить скалярное произведение векторов 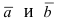 , если их длины равны 2 и 5, соответственно, а угол между векторами равен
, если их длины равны 2 и 5, соответственно, а угол между векторами равен 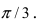
Решение:
Используя определение скалярного определения, находим 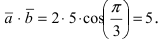
Замечание: Используя определения проекции (см. Лекция № 2) и скалярного произведения двух векторов, можно записать, что 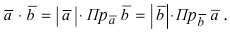 Откуда можно найти проекцию одного вектора на другой, например,
Откуда можно найти проекцию одного вектора на другой, например, 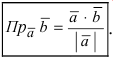
Пример:
Найти 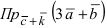 и
и 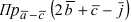 (координаты векторов
(координаты векторов 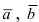 и
и 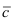 ).
).
Решение:
Введём новые векторы:
Так как проекция одного вектора на другой определяется формулой 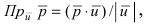 вычислим скалярное произведение
вычислим скалярное произведение 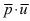 и длину вектора
и длину вектора 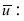
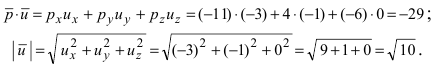
Следовательно, 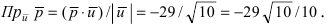 Поступая аналогичным образом, найдем
Поступая аналогичным образом, найдем

вычислим скалярное произведение 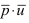 и длину вектора
и длину вектора 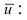
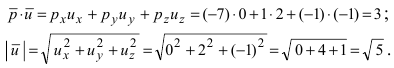
Отсюда находим, что 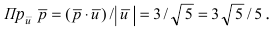
Рассмотрим свойства скалярного произведения:
- 1.
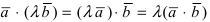 ;
; - 2.
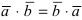 ;
; - 3.
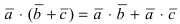 ;
; - 4.
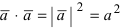 ;
; - 5. Если вектор
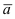 перпендикулярен вектору
перпендикулярен вектору 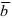 (
(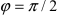 ), то их скалярное произведение равно нулю:
), то их скалярное произведение равно нулю: 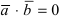 .
.
Замечание: Свойство 5. определяет условие перпендикулярности векторов.
Формула для скалярного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть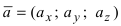 и
и 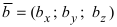 . Тогда
. Тогда 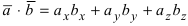 .
.
Доказательство: Запишем вектора 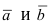 в декартовом базисе:
в декартовом базисе: 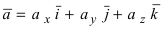 и
и 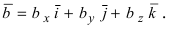 Для доказательства формулы теоремы составим таблицу скалярных произведений ортов осей:
Для доказательства формулы теоремы составим таблицу скалярных произведений ортов осей:
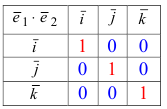
Используя эту таблицу, вычислим скалярное произведение векторов 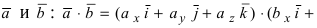
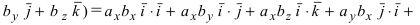
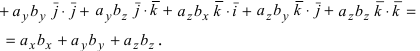
Следствие: Если вектор 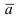 перпендикулярен вектору
перпендикулярен вектору 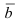 (
(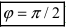 ), то их скалярное произведение равно нулю, т.е.
), то их скалярное произведение равно нулю, т.е. 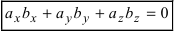
Следствие: Если 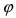 - угол между векторами
- угол между векторами 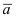 и
и 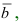 то
то 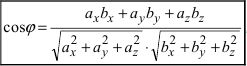
Следствие: Проекция вектора 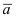 на произвольную ось (U) равна скалярному произведению вектора
на произвольную ось (U) равна скалярному произведению вектора 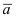 на орт этой оси:
на орт этой оси: 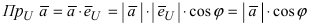 .
.
Пример:
Найти, при каком значении m вектора 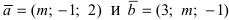 перпендикулярны.
перпендикулярны.
Решение:
Условием перпендикулярности векторов является обращение в нуль их скалярного произведения, поэтому воспользуемся следствием 1 из теоремы 2:
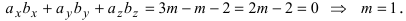
Применение скалярного произведения
1. Физика. Пусть под воздействием силы 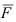 некоторое тело совершает перемещение
некоторое тело совершает перемещение 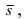 тогда работа, совершенная над телом, равна
тогда работа, совершенная над телом, равна 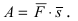
2. Тригонометрия, а) Теорема косинусов: рассмотрим произвольный треугольник АВС , в котором введем вектора 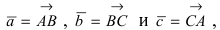 тогда
тогда 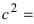
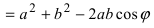 (Рис. 1 1):
(Рис. 1 1):
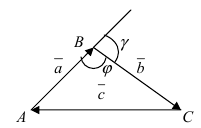
Рис. 11. Теорема косинусов для произвольного треугольника.
Доказательство: 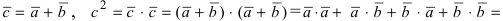 (используя свойства 2. и 4. для скалярного произведения векторов, найдем)
(используя свойства 2. и 4. для скалярного произведения векторов, найдем)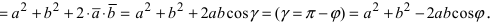 б) Косинус суммы двух углов: пусть в плоской декартовой системе координат даны вектора
б) Косинус суммы двух углов: пусть в плоской декартовой системе координат даны вектора 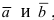 которые образуют с положительным направлением оси Ох углы
которые образуют с положительным направлением оси Ох углы 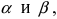 соответственно (Рис. 12):
соответственно (Рис. 12):
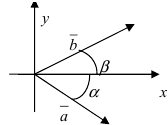
Рис. 12. Косинус суммы двух углов.
Тогда 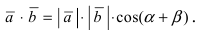 С другой стороны, аффинные координаты векторов равны
С другой стороны, аффинные координаты векторов равны 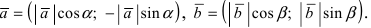 Используя формулу для скалярного произведения векторов
Используя формулу для скалярного произведения векторов 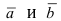 через проекции перемножаемых векторов, получим
через проекции перемножаемых векторов, получим 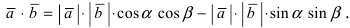 Сравнивая полученные формулы, находим формулу для косинуса суммы 2 углов
Сравнивая полученные формулы, находим формулу для косинуса суммы 2 углов
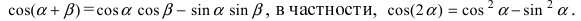
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |