
Формулы Крамера - определение и вычисление с примерами решения
Содержание:
Формулы Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А 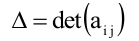
Формулы Крамера имеют вид: 
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
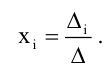
Если главный определитель системы  и все вспомогательные определители
и все вспомогательные определители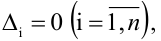 то система имеет бесчисленное множество решений. Если главный определитель системы
то система имеет бесчисленное множество решений. Если главный определитель системы 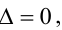 а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Пример:
Решить методом Крамера систему уравнений: 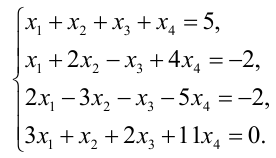
Решение:
Главный определитель этой системы 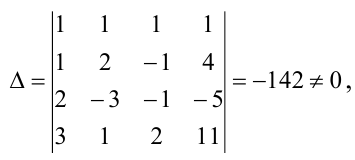 значит, система имеет единственное решение.
значит, система имеет единственное решение.
Вычислим вспомогательные определители 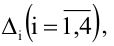 получающиеся из определителя
получающиеся из определителя  путем замены в нем столбца, состоящего из коэффициентов при
путем замены в нем столбца, состоящего из коэффициентов при 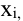 столбцом из свободных членов:
столбцом из свободных членов:
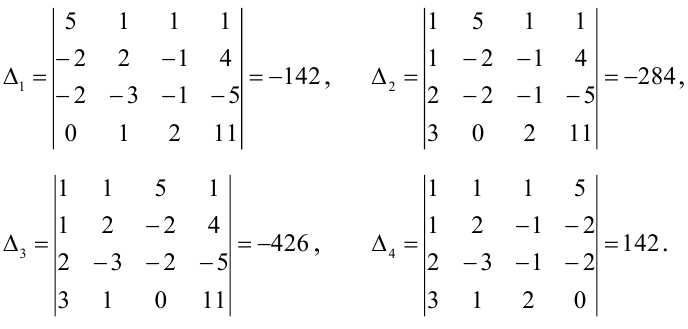 Отсюда
Отсюда 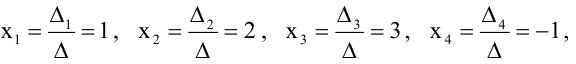
решение системы - вектор 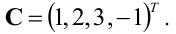
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |