Асимптоты графика функции с примерами решения
Содержание:
Понятие асимптоты:
Асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Вертикальные асимптоты 
 — вертикальная асимптота, если при
— вертикальная асимптота, если при 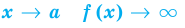
Вертикальная асимптота 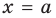 может быть в точке
может быть в точке 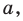 если точка
если точка 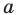 ограничивает открытые (или полуоткрытые) промежутки области определения данной функции и вблизи точки
ограничивает открытые (или полуоткрытые) промежутки области определения данной функции и вблизи точки 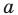 значения функции стремятся к бесконечности.
значения функции стремятся к бесконечности.
Примеры вертикальных асимптот графиков функций
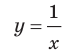
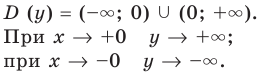
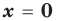 — вертикальная асимптота (
— вертикальная асимптота (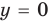 — также асимптота, но горизонтальная)
— также асимптота, но горизонтальная)
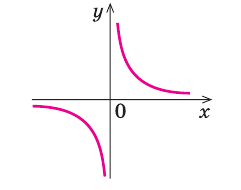
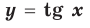
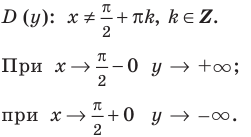
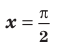 — вертикальная асимптота
— вертикальная асимптота
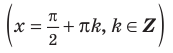
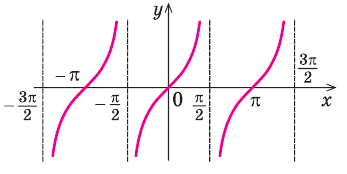
Наклонные и горизонтальные асимптоты 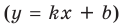
I. Если 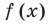 — дробно рациональная функция, у которой степень числителя на единицу больше степени знаменателя (или равна ей), то выделяем целую часть дроби и используем определение асимптоты.
— дробно рациональная функция, у которой степень числителя на единицу больше степени знаменателя (или равна ей), то выделяем целую часть дроби и используем определение асимптоты.
Примеры:
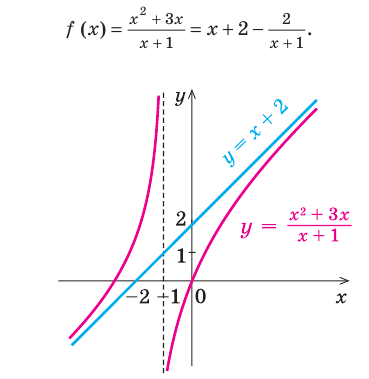
При 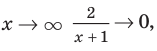 тогда
тогда 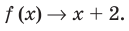 Следовательно,
Следовательно, 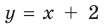 — наклонная асимптота (также
— наклонная асимптота (также 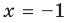 — вертикальная асимптота)
— вертикальная асимптота)
При 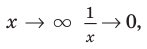 тогда
тогда 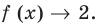 Следовательно,
Следовательно, 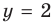 — горизонтальная асимптота (также
— горизонтальная асимптота (также 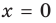 — вертикальная асимптота)
— вертикальная асимптота)
II. В общем случае уравнения наклонных и горизонтальных асимптот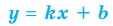 можно получить с использованием формул
можно получить с использованием формул
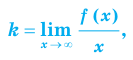
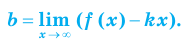
Понятие асимптоты
Если кривая 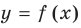 имеет бесконечную ветвь, то асимптотой такой кривой называют прямую, к которой эта ветвь неограниченно приближается. Другими словами, асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
имеет бесконечную ветвь, то асимптотой такой кривой называют прямую, к которой эта ветвь неограниченно приближается. Другими словами, асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Асимптоты могут быть вертикальными, горизонтальными или наклонными.
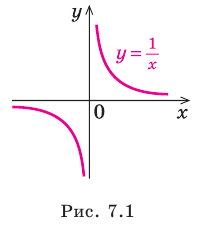
Например, для графика функции 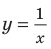 (рис. 7.1) асимптотами будут оси координат, поскольку при
(рис. 7.1) асимптотами будут оси координат, поскольку при 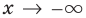 и при
и при 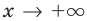 график функции приближается к прямой
график функции приближается к прямой 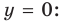 ось
ось 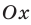 — горизонтальная асимптота. Когда функция стремится к
— горизонтальная асимптота. Когда функция стремится к 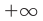 (или
(или 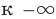 ), то кривая приближается к прямой
), то кривая приближается к прямой 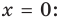 ось
ось 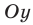 — вертикальная асимптота.
— вертикальная асимптота.
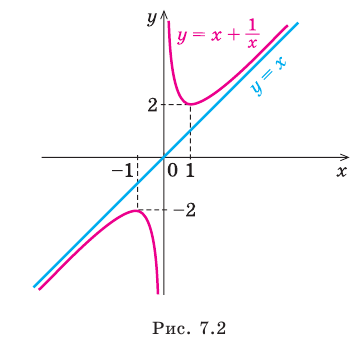
Если рассмотреть функцию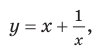 то при
то при 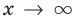 выражение
выражение 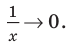 Вследствие этого график функции
Вследствие этого график функции 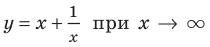 приближается к прямой
приближается к прямой 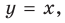 поэтому эта прямая будет наклонной асимптотой графика функции
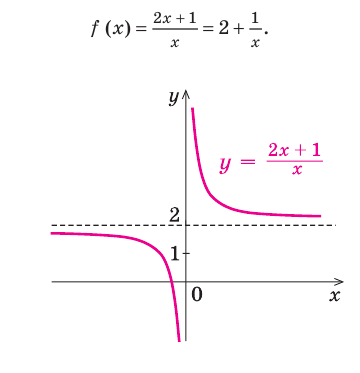
поэтому эта прямая будет наклонной асимптотой графика функции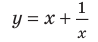 (рис. 7.2) (график этой функции имеет также и вертикальную асимптоту
(рис. 7.2) (график этой функции имеет также и вертикальную асимптоту 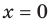 ).
).
Следует отметить, что не любая кривая имеет асимптоту, поэтому не у каждого графика функции будет асимптота. Но исследование функции на наличие у ее графика асимптот позволяет уточнить свойства функции и поведение ее графика.
Вертикальные асимптоты
Если прямая 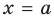 — вертикальная асимптота, то по определению около точки
— вертикальная асимптота, то по определению около точки 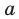 кривая должна иметь бесконечную ветвь, то есть предел данной функции при
кривая должна иметь бесконечную ветвь, то есть предел данной функции при  (слева или справа) должен равняться бесконечности (
(слева или справа) должен равняться бесконечности (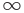 ). Исходя из непрерывности элементарных функций, которые рассматривались в школьном курсе математики, такими точками могут быть только точки, ограничивающие открытые (или полуоткрытые) промежутки области определения данной функции.
). Исходя из непрерывности элементарных функций, которые рассматривались в школьном курсе математики, такими точками могут быть только точки, ограничивающие открытые (или полуоткрытые) промежутки области определения данной функции.
Например, у функции 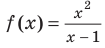 область определения
область определения 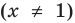 имеет разрыв в точке
имеет разрыв в точке  (область определения:
(область определения: 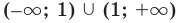 и точка 1 ограничивает открытые промежутки области определения). Можно предположить, что прямая
и точка 1 ограничивает открытые промежутки области определения). Можно предположить, что прямая  будет вертикальной асимптотой. Для того чтобы убедиться в этом, необходимо проверить, будет ли функция стремиться к бесконечности около точки 1 (слева или справа). Для этого рассмотрим
будет вертикальной асимптотой. Для того чтобы убедиться в этом, необходимо проверить, будет ли функция стремиться к бесконечности около точки 1 (слева или справа). Для этого рассмотрим
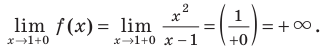
Аналогично 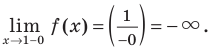
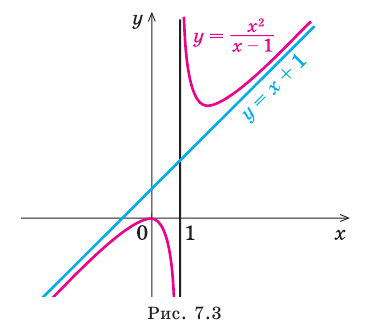
Таким образом, прямая  является вертикальной асимптотой, поскольку при стремлении функции к бесконечности ее график неограниченно приближается к прямой
является вертикальной асимптотой, поскольку при стремлении функции к бесконечности ее график неограниченно приближается к прямой  (рис. 7.3).
(рис. 7.3).
Отметим, что не всегда в точке разрыва области определения функция будет иметь вертикальную асимптоту. Например, функция 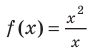 имеет область определения
имеет область определения 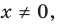 поэтому прямая
поэтому прямая 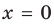 «подозрительна» на вертикальную асимптоту. Но
«подозрительна» на вертикальную асимптоту. Но 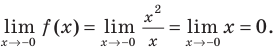 Аналогично
Аналогично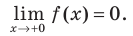 Следовательно, около прямой
Следовательно, около прямой 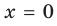 функция
функция 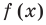 не стремится к бесконечности, и поэтому прямая
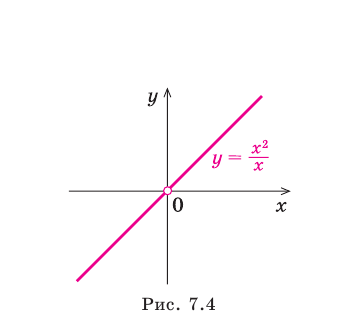
не стремится к бесконечности, и поэтому прямая 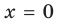 не является асимптотой графика данной функции (рис. 7.4).
не является асимптотой графика данной функции (рис. 7.4).
Наклонные и горизонтальные асимптоты
Наклонные и горизонтальные асимптоты довольно просто находятся для графиков дробно-рациональных функций, у которых степень числителя на единицу больше степени знаменателя (или равна степени знаменателя). Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
Например, еще раз рассмотрим функцию 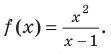 Выделим целую часть:
Выделим целую часть: 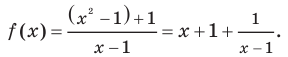
При 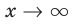 выражение
выражение 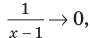 то есть график нашей функции будет х -1 неограниченно приближаться к прямой
то есть график нашей функции будет х -1 неограниченно приближаться к прямой 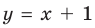 при
при 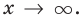 Из этого следует, что наклонной асимптотой графика данной функции* будет прямая
Из этого следует, что наклонной асимптотой графика данной функции* будет прямая 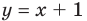 (рис. 7.3).
(рис. 7.3).
Рассмотрим, как находятся наклонные и горизонтальные асимптоты в общем случае.
Пусть наклонной (или горизонтальной) асимптотой графика функции 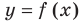 является прямая
является прямая  По определению асимптоты при
По определению асимптоты при 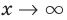 график функции
график функции 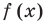 неограниченно приближается к прямой
неограниченно приближается к прямой 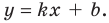 Другими словами, при
Другими словами, при 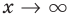 с любой точностью будет выполняться равенство
с любой точностью будет выполняться равенство
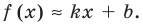 (1)
(1)
Эта равенство не нарушится, если обе его части разделить на 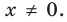 Получим:
Получим: 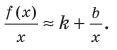 При
При 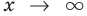 отношение
отношение 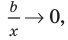 поэтому отношение
поэтому отношение 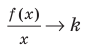 при
при 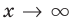 , то есть
, то есть
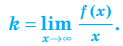 (2)
(2)
Возвращаясь к формуле (1), получаем, что при 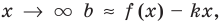 то есть
то есть
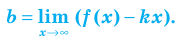 (3)
(3)
Формулы (2) и (3) дают возможность находить наклонные и горизонтальные асимптоты для графика любой функции 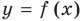 (при условии, что они существуют).
(при условии, что они существуют).
Отметим, что если у графика функции 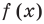 есть горизонтальная асимптота, то ее уравнение будет
есть горизонтальная асимптота, то ее уравнение будет 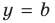 (в этом случае
(в этом случае 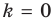 ). Но при
). Но при 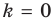 из формулы (3) получаем
из формулы (3) получаем 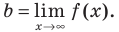 Следовательно, если существует число
Следовательно, если существует число 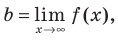 то график функции
то график функции 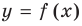 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 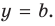
Пример:
Пользуясь общими формулами, найдите наклонную асимптоту графика функции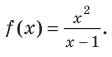
Решение:
Будем искать наклонную асимптоту в виде 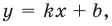 где
где 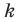 и
и 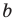 находятся по формулам (2) и (3):
находятся по формулам (2) и (3):
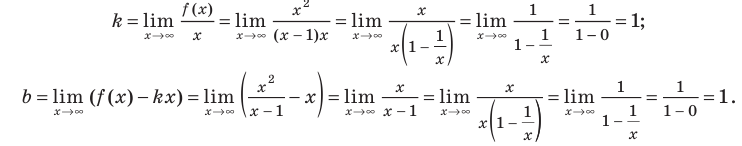
Асимптотой графика данной функции будет прямая 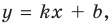 то есть прямая
то есть прямая 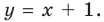
Пример:
Найдите асимптоты графика функции 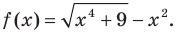
Решение:
Область определения функции: 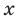 — любое действительное число, то есть
— любое действительное число, то есть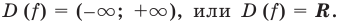 На всей области определения эта функция непрерывна, поэтому вертикальных асимптот график функции не имеет. Будем искать наклонные и горизонтальные асимптоты в виде
На всей области определения эта функция непрерывна, поэтому вертикальных асимптот график функции не имеет. Будем искать наклонные и горизонтальные асимптоты в виде 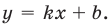 Тогда
Тогда
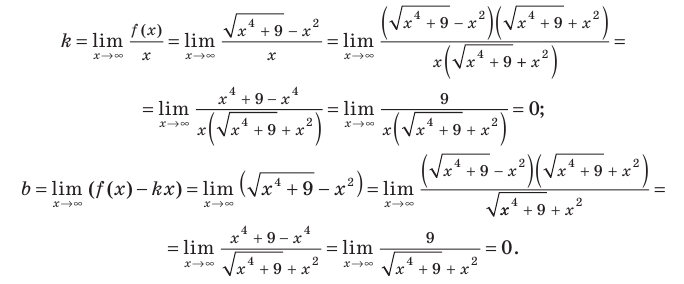
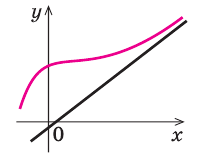
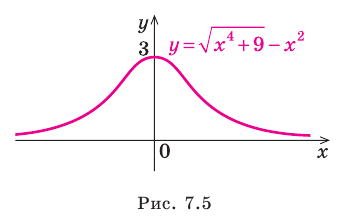
Таким образом, заданная функция имеет только горизонтальную асимптоту 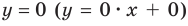 (рис. 7.5).
(рис. 7.5).
Иногда график функции 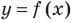 может иметь разные асимптоты при
может иметь разные асимптоты при 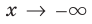 и при
и при 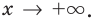 в этом случае при использовании формул (2) и (3) приходится отдельно находить значения
в этом случае при использовании формул (2) и (3) приходится отдельно находить значения 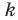 и
и 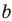 при
при 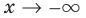 и при
и при 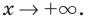
Как найти асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 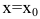 называется вертикальной асимптотой графика функции y=f(x), если хотя бы один из односторонних пределов в точке
называется вертикальной асимптотой графика функции y=f(x), если хотя бы один из односторонних пределов в точке 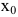 равен бесконечности:
равен бесконечности: 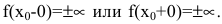 Такие асимптоты существуют только в точках разрыва второго рода.
Такие асимптоты существуют только в точках разрыва второго рода.
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы
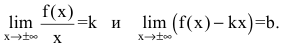
Частным случаем наклонной асимптоты (k=0) является горизонтальная асимптота.
Пример:
Найти асимптоты графика функции 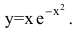
Решение:
Функция 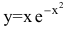 непрерывна в области определения
непрерывна в области определения 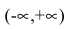 как элементарная. Следовательно, вертикальных асимптот нет. Найдем наклонные асимптоты y=kx+b:
как элементарная. Следовательно, вертикальных асимптот нет. Найдем наклонные асимптоты y=kx+b:
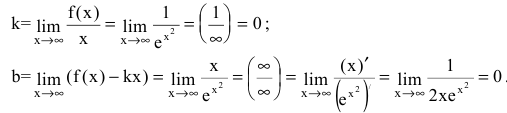
Получаем горизонтальную асимптоту y=0.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции D(f).
- Исследовать функцию на четность
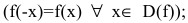 нечетность
нечетность 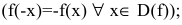 периодичность
периодичность 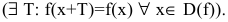
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример:
Провести полное исследование функции 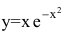 и построить ее график.
и построить ее график.
Решение:
Область определения функции - вся числовая прямая: 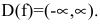
Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и 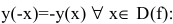
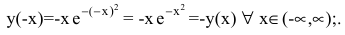
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для 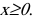
Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 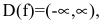 точек разрыва нет.
точек разрыва нет.
Строим график функции, используя результаты исследования.
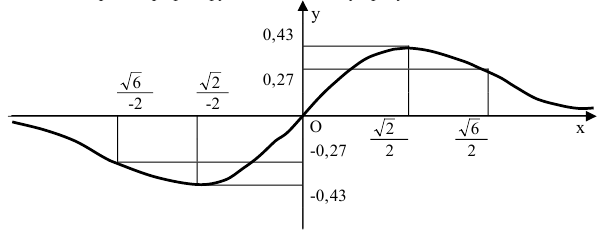
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |