Медианы, высоты и биссектрисы треугольника - определение и вычисление с примерами решения

Рассмотрим понятия медианы, высоты и биссектрисы треугольника.

Определение. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Любой треугольник имеет три медианы.

Например, если точки A_1, B₁ и C₁  — соответственно середины сторон ВС, СА и АВ треугольника АВС, то отрезки AA₁, ВB₁ и CC₁ — медианы этого треугольника (рис. 69, а).

Если точки F и Т — середины ребер B₁C₁ и A₁C₁ прямой призмы ABCA₁B₁C₁, тогда отрезки B₁Т и A₁F — медианы треугольника A₁B₁C₁, служащего основанием призмы (рис. 69, б, в).

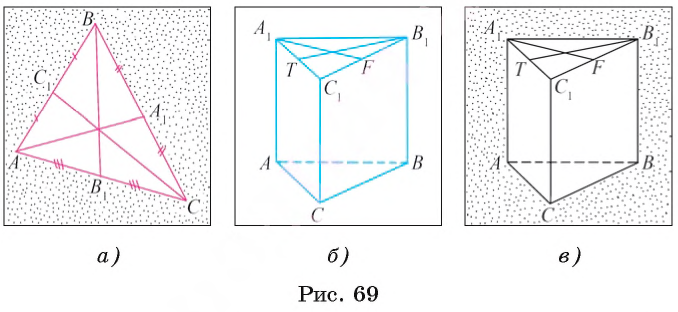
Медианы, проведенные из вершин А, В и С треугольника ABC (или их длины), можно обозначить m_a, m_b и m_c соответственно.

Определение. Высотой треугольника называется перпендикуляр, проведенный из его вершины к прямой, содержащей противолежащую сторону.

Любой треугольник имеет три высоты. На рисунке 70, а, б, в изображены отрезки AF₁, BF₂ и CF₃, которые являются высотами треугольника ABC.

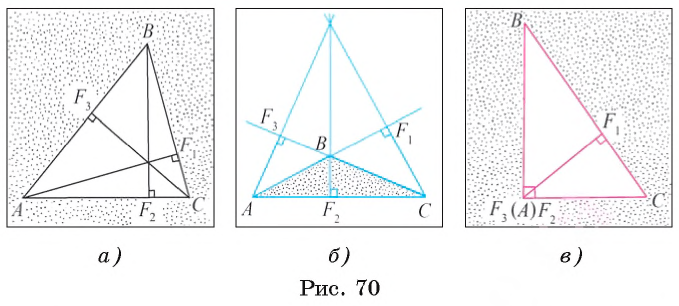
Высоты, проведенные из вершин А, В и С треугольника ABC (или их длины), можно обозначить h_a, h_b и h_c соответственно.

Иногда вместо «вычислите длину высоты треугольника» можно говорить «вычислите высоту треугольника».

Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны.

На рисунке 71, а изображена биссектриса СЕ треугольника ABC. Любой треугольник имеет три биссектрисы. На рисунке 71, B изображены биссектрисы АЕ₁, ВЕ₂ и CE₃ треугольника ABC.

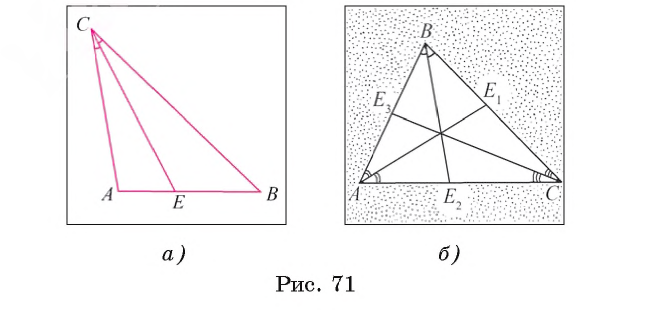
Биссектрисы, проведенные из вершин А, В и С треугольника ABC (или их длины), можно обозначить l_а, l_b и l_c соответственно.

В дальнейшем будет доказано, что медианы, высоты и биссектрисы в любом треугольнике обладают следующими свойствами:

• медианы пересекаются в одной точке;
• высоты или прямые, содержащие высоты, пересекаются в одной точке;
• биссектрисы пересекаются в одной точке.