Равнобедренный треугольник и его свойства - определение и вычисление с примерами решения

Среди множества треугольников выделяются треугольники, имеющие особые свойства. К ним относятся, например, равнобедренные треугольники.

Определение. Треугольник называется равнобедренным, если две его стороны равны.

Равные стороны равнобедренного треугольника называются боковыми сторонами, а третья сторона называется основанием равнобедренного треугольника.

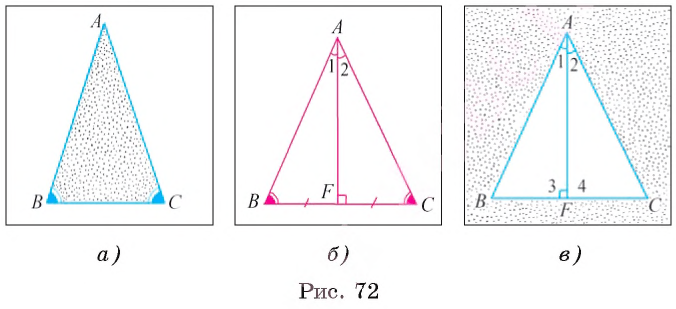
Если в равнобедренном треугольнике ABC равны стороны АС и AB, то точка А называется вершиной равнобедренного треугольника, а точки В и С — вершинами при его основании. Угол А называется углом при вершине, а углы B и С — углами при основании (рис. 72, а).

Определение. Треугольник, все стороны которого равны, называется равносторонним.

Заметим, что из данных определений следует, что любой равносторонний треугольник является также и равнобедренным.

Теперь докажем некоторые теоремы о свойствах равнобедренного треугольника.

Теорема 3 (о свойстве углов при основании равнобедренного треугольника). В равнобедренном треугольнике углы при основании равны.

Доказательство.

1) Пусть ABC — равнобедренный треугольник, боковые стороны которого АС и AB. Докажем, что (рис. 72, б).

2) Пусть отрезок AF — биссектриса треугольника ABC. Тогда треугольники ABF и ACF равны по первому признаку равенства треугольников (АС = AB по условию, сторона AF — общая, 1 = 2, так как AF — биссектриса треугольника ABC).

3) Из равенства треугольников ABF и ACF следует, что B = C.

Теорема доказана.

Теорема 4 (о свойстве биссектрисы, проведенной к основанию равнобедренного треугольника).

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Доказательство.

1. Пусть ABC — равнобедренный треугольник, у которого АС = AB, отрезок AF — биссектриса этого треугольника. Докажем, что отрезок АF является медианой и высотой этого треугольника (рис. 72, в).
2. Треугольники АВF и АСF равны по первому признаку равенства треугольников (АС = АВ по условию, сторона АF — общая, 1 = 2).
3. Из равенства треугольников АВF и АСF следует, что ВF = FC, т. е. точка F — середина стороны ВС, а, значит, отрезок АF — медиана треугольника АВС.
4. Из равенства треугольников АВF и АСF также следует, что 3 = 4. Так как углы 3 и 4 смежные и равные, то они прямые. Отсюда следует, что отрезок АF — высота треугольника АВС.

Теорема доказана.

Из факта совпадения в равнобедренном треугольнике биссектрисы, медианы и высоты следуют утверждения.

1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.