Серединный перпендикуляр к отрезку - определение и вычисление с примерами решения

Серединный перпендикуляр к отрезку:

Рассмотрим понятие серединного перпендикуляра к отрезку.

Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

Следующая теорема характеризует свойства точек серединного перпендикуляра к отрезку.

Теорема 5 (о серединном перпендикуляре). Каждая точка серединного перпендикуляра к отрезку находится на равном расстоянии от концов этого отрезка. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство.

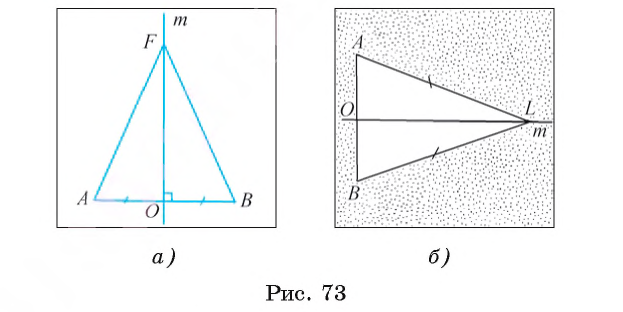
1) Пусть прямая m — серединный перпендикуляр к отрезку АВ, точка О — середина отрезка АВ (рис. 73, а).

Пусть точка F — произвольная точка серединного перпендикуляра. Докажем, что FА = FВ. Если точка F совпадает с точкой О, то это равенство верно, так как точка О — середина отрезка АВ. Пусть точка F не совпадает с точкой О. В этом случае треугольник АОF равен треугольнику ВОF по первому признаку равенства треугольников (АО = ОВ по условию, сторона ОF — общая, 90°). Отсюда следует, что АF = ВF.

2) Пусть точка L равноудалена от концов отрезка АВ, т. е. АL = ВL (рис. 73, б). Докажем, что точка L лежит на прямой m. Если точка L лежит на прямой АВ, то она совпадает с серединой О отрезка АВ, т. е. лежит на прямой m. Если точка В не лежит на прямой АВ, то треугольник АLВ равнобедренный. Отрезок LO — медиана этого треугольника, а следовательно, и высота. Таким образом, LО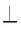АВ, а, значит, прямые LО и m совпадают. Отсюда вытекает, что точка L лежит на прямой m.

Теорема доказана.