Потенциальная энергия в теоретической механике

Содержание:

Потенциальное силовое поле и силовая функция:

Силовым полем называют часть пространства, приведенную какими-либо телами в такое состояние, при котором в каждой ее точке на данную материальную частицу действует сила, зависящая только от положения частицы и от времени, но не от ее скорости

Силовое поле

Пусть к материальной частице находящейся внутри некоторой области (части пространства), приложена сила, обусловленная наличием каких-либо тел. Если материальная частица передвигается в этой области, то действующая на нее сила может изменяться в зависимости от положения частицы или же оставаться постоянной. Эта сила может изменяться и со временем, но не должна зависеть от скорости частицы. Такую часть пространства называют силовым полем, причем силовое поле называют стационарным, если силы его не зависят от времени, и нестационарным, если силы поля с течением времени меняются.

Так, например, наша планета находится под действием силы притяжения к Солнцу. Эта сила обратно пропорциональна квадрату расстояния Земли от Солнца, т. е. зависит от положения Земли относительно Солнца, но не зависит от времени, и поле тяготения к Солнцу является стационарным силовым полем.

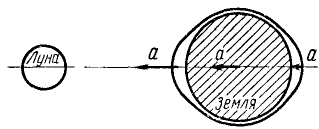
Тяготением Ньютон объяснил (1687 г.) морские приливы и отливы. Его теория, усовершенствованная главным образом Д. Бернулли, рассматривает океан как водяной покров, окружающий твердый земной шар. Капли воды, находящиеся ближе к Луне, притягиваются к ней сильнее, чем более удаленные капли. Вследствие «приливного ускорения» (рис. 221), т. е. геометрической разности ускорений, которые Луна сообщает центру земного шара и каплям водяной оболочки Земли, возникает движение воды такого характера, как будто обращенная к Луне часть океана притягивается ею, а противоположная отталкивается. Поэтому навстречу вращению Земли (т. е. с В на 3) всегда бежит по океану приливная волна (но не течение!). Аналогичное явление получается от притяжения к Солнцу, но расстояние до Солнца так велико по сравнению с размерами Земли, что приливное ускорение от притяжения к Солнцу составляет всего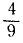

Силовой функцией называют такую функцию координат точек стационарного поля, полный дифференциал которой равен элементарной работе сил поля

Силовая функция силового поля

Дано какое-либо стационарное поле и пусть существует некоторая функция координат 

U = U (х, у, г),    (237)

обладающая тем свойством, что ее частные производные по х, у и г являются однозначными функциями координат и равны проекциям X, Y и Z силы поля на соответствующие оси координат, т.е.

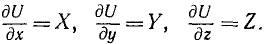    (238)

Функцию U называют силовой функцией, а силу 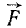поля, проекции которой на оси равны частным производным от силовой функции по этим осям, называют градиентом силовой функции:

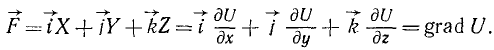    (239)

Геометрическое место точек, в которых силовая функция имеет одинаковое значение

U (х, у, z) = const    (240)

называют эквипотенциальной поверхностью, или поверхностью уровня. Все силовое поле можно представить заполненным непрерывным множеством бесконечно близких друг другу поверхностей уровня. Для каждого мгновения существуют определенные поверхности уровня и в нестационарных силовых полях

U (х, у, z, t) = const.    (240')

Во всякой точке поля градиент (239) направлен по нормали к поверхности уровня.

Подставив в выражение (221) элементарной работы вместо X, Y и Z эти значения, получим

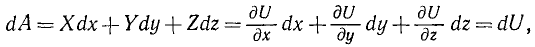
т. е. элементарная работа силы поля равна полному дифференциалу силовой функции

 dA=dU    (241)

Для существования силовой функции должны удовлетворяться определенные соотношения между проекциями силы поля. Продифференцируем по z второе из равенств (238), а третье продифференцируем по у, получим

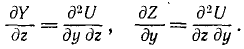
Ha основании свойств частных производных можем написать следующие равенства:

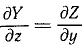 и аналогично  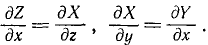  (242)

Задача №1

Существует ли силовая функция в стационарном силовом поле, если проекции силы поля на оси координат зависят от координат материальной точки следующим образом X-2xy; Y =x²; Z = 0?

Решение. Для ответа на вопрос воспользуемся равенством (242)

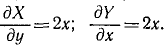
Следовательно, условия (242) выполняются.
Ответ. Да, существует.

Потенциальным полем называют такое стационарное силовое поле, в котором работа силы поля, приложенной к материальной частице, зависит только от начального и конечного положений этой частицы

Потенциальное силовое поле

Стационарное поле, в котором выполняются эти условия, т. е. имеется силовая функция U, называют потенциальным полем. Пусть в потенциальном поле движется материальная частица, перемещающаяся с произвольной скоростью и безразлично по какой траектории из одного положения, которое мы примем за начальное, в какое-либо другое, которое мы назовем конечным. Обозначим через U₀ значение силовой функции в той точке поля, которую мы приняли за начальное положение частицы, а через U — в конечной точке и затем, проинтегрировав левую и правую части равенства (241) в соответствующих пределах от 0 до А и от U₀ до U, получим

A = U- U₀.   (243)

Таким образом, независимо от скорости частицы и формы траектории работа силы потенциального поля равна разности значений силовой функции в конечной и в начальной точках траектории. Пусть имеется такое положение точки, для которого значение силовой функции равно нулю. Назовем это положение нулевым и примем его за начальное (U₀ = 0). В таком случае

A = U

Следовательно, силовая функция выражает ту работу, которую производит сила поля при переходе материальной частицы из нулевого положения в данное.

Потенциальная энергия материальной точки равна работе сил потенциального поля при переходе точки из данного положения в нулевое

Потенциальная энергия материальной частицы

Наряду с силовой функцией U нам понадобится величина П, связанная с силовой функцией простой зависимостью

П = - U    (244)

и называемая потенциальной энергией.

Равенство (244) вместе с предыдущим равенством позволяют выяснить физическую сущность этого понятия: потенциальная энергия материальной точки, находящейся в каком-либо данном положении, равна работе силы потенциального поля при переходе точки из данного положения в нулевое.
Поясним это следующими примерами.

Потенциальная энергия пружины

Сжатая пружина обладает потенциальной энергией, обусловленной упругими деформациями в материале пружины. Если пружина сжата на величину х, то, как было показано (227), при переходе ее в ненапряженное состояние сила упругости может совершить работу 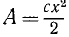. Эта способность сжатой пружины совершить работу является потенциальной энергией пружины:

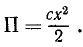
Так же выразится и потенциальная энергия растянутой пружины.

Потенциальная энергия тела в поле тяжести

Материальная частица или тяжелое тело, поднятое на некоторую высоту, обладает потенциальной энергией, равной той работе, которую совершит сила тяжести при опускании тела до «нулевого положения». Однако нулевое положение в поле силы тяжести не может быть так естественно определено, как в поле упругой силы. Для пружины и вообще в случаях упругих сил нулевым положением является то, при котором отсутствует деформация. Для тяжелого тела нулевым положением может быть уровень пола, уровень земли и т. д. Уровень, относительно которого отсчитывают потенциальную энергию тела, поднятого на некоторую высоту, может быть выбран совершенно условно. Но эта условность в выборе нулевого положения не сказывается на расчетах, так как в расчеты всегда входит не полная потенциальная энергия, а ее изменение. Нужно лишь отсчитывать потенциальную энергию относительно одного и того же уровня. Поэтому для определения потенциальной энергии тела в поле силы тяжести мы построим систему прямоугольных координатных осей, направив ось Oz вертикально вверх, но не будем пока уточнять положение начала отсчета и определим проекции силы тяжести:

X = O; У = 0; Z = -G.

Условия (242) существования силовой функции удовлетворяются. Определим дифференциал силовой функции:

Xdx + Ydy + Zdz = — Gdz — dU.

Интегрируя, найдем силовую функцию силы тяжести:

U = - Gz+ C.

Постоянная интеграции C зависит от начала отсчета, но изменение U-U₀ силовой функции от начала отсчета не зависит. Интегрирование можно провести и в пределах. Выберем, например, за нулевое положение уровень моря и пусть тело поднято на высоту h, тогда

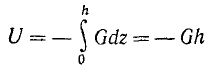
и

П = + Gh.

Нетрудно видеть, что изменение П—П₀ потенциальной энергии тела при заданном изменении его высоты одинаково, выразим ли мы ее как П=Gh или П = Gz+С, и не зависит от С.

Силовая функция поля всемирного тяготения

По закону всемирного тяготения планеты притягиваются к Солнцу с силой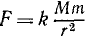 , где M — масса Солнца, m—масса планеты и k— постоянная величина. Построив систему координат с началом в центре Солнца (рис. 222), определим проекции силы на оси, для чего умножим модуль силы на ее направляющие косинусы:

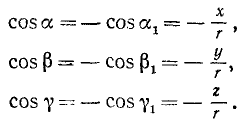
Получим 

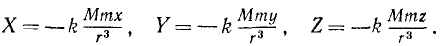
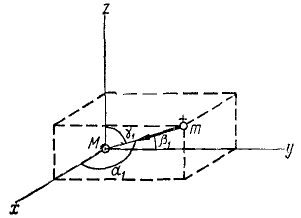
Рис. 222

Взяв частные производные от этих величин по х, у и г, можно показать, что условия (242) существования силовой функции выполняются, а следовательно, силовая функция существует. Найдем эту функцию:

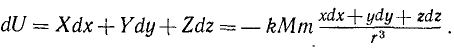
Числитель дроби в правой части есть rdr, в чем можно убедиться, продифференцировав равенство r² = x² + y² + z^2, поэтому

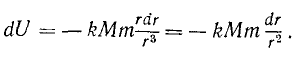
Интегрируя, находим силовую функцию ньютонианского поля:
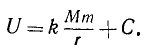   (245)

Или, если ввести гауссово число μ-kM, то

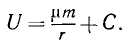     (245')

Потенциальная энергия выражается той же величиной, но взятой с обратным знаком.

При движении материальной частицы под действием силы потенциального поля сумма кинетической и потенциальной энергий частицы остается постоянной

Закон сохранения механической энергии

На материальную частицу, находящуюся в потенциальном поле, действует сила этого поля, поэтому при движении частицы ее скорость, а следовательно, и кинетическая энергия ее в общем случае меняются. Выражая в уравнении (232) работу А равенством (243), найдем зависимость изменения кинетической энергии от изменения силовой функции:

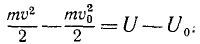     (246)

Это равенство называют интегралом кинетической энергии. Оно показывает, что изменение кинетической энергии материальной частицы, движущейся в потенциальном поле, равно изменению силовой функции, не зависит от пути материальной частицы, а зависит лишь от ее начального и конечного положений в потенциальном поле.

Если в равенстве (246) силовую функцию мы выразим посредством (244) через потенциальную энергию, то получим

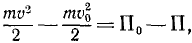
откуда

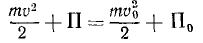
и вообще

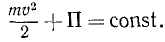     (247)

Таким образом, если материальная частица движется в потенциальном поле под действием сил этого поля, то во всякое мгновение при всяком положении частицы сумма ее кинетической и потенциальной энергий есть величина постоянная. Равенство (247) выражает закон сохранения механической энергии и имеет применение в тех случаях, если на частицу не действуют никакие силы, кроме сил потенциального поля. Поэтому потенциальные поля называют также консервативными (от лат. Conservativus—сохраняющий).

Так, например, закон сохранения механической энергии справедлив при движении планет в поле ньютонианского тяготения: чем ближе к Солнцу находится планета на своей эллиптической орбите, тем меньше ее потенциальная энергия и соответственно больше кинетическая (см. § 44 — закон площадей). Скорость периодических комет, движущихся по очень вытянутым эллипсам, в перигелии во много тысяч раз превышает их скорость в афелии, но в любой точке орбиты сумма кинетической и потенциальной энергий кометы есть для этой кометы величина постоянная.

Вывод первого закона Кеплера из закона всемирного тяготения Ньютона

Задача №2

Определить траекторию небесного тела (планеты, кометы, космического корабля), движущегося под действием тяготения к Солнцу, подчиняясь закону всемирного тяготения Ньютона.
Решение. Задача относится к обратным задачам динамики: определить движение по заданной силе. Для решения воспользуемся интегралом кинетической энергии

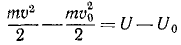      (246)

или, применительно к данной задаче и в виду (245')

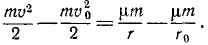
Определим из этого равенства υ₂ и заменим радиус-вектор его обратной величиной :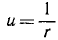

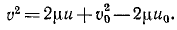
Для упрощения записи введем обозначение

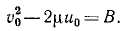
Тогда

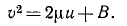
Это значение υ₂ внесем в первую формулу Бине (191):

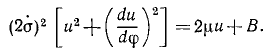
Решим это уравнение относительно dφ:

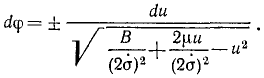
Если мы отсчитываем φ от какого-либо начального положения, в котором радиус-вектор возрастает, а следовательно, его обратная величина 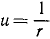 убывает, то du имеет отрицательный знак и

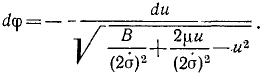
Для интегрирования преобразуем выражение, стоящее под знаком корня, прибавив к подкоренному количеству и вычтя из него :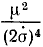

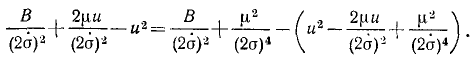
Выражение, взятое в скобки, представляет полный квадрат разности двух количеств, и радикал принимает следующий вид:

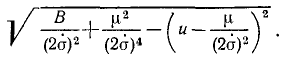
Сумма двух первых членов в подкоренном количестве должна быть больше отрицательного третьего члена, потому что в противном случае φ было бы мнимой величиной. Введем обозначение

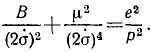
Положим, кроме того, как это мы уже приняли при решении задачи № 129, что 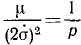и перепишем уравнение в следующем виде:

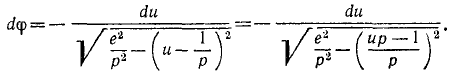
Разделим числители и знаменатели на :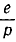

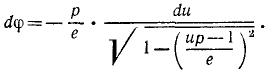
В правой части равенства мы имеем дифференциал арккосинуса от аргумента 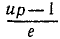. Теперь интегрирование не составляет труда и, учитывая, что постоянная интеграции равна нулю, получаем

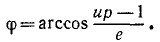
Решим это уравнение относительно :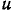

Мы получили уравнение конического сечения в полярных координатах.

Ответ.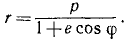. Траектория—коническое сечение.

Задача №3

По данным предыдущей задачи определить условия, при которых траекторией небесного тела является эллипс, парабола или гипербола.

Решение. В обозначениях, принятых в предыдущей задаче, напишем:

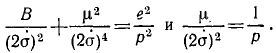
Как видно из конечного результата предыдущей задачи, величины р и e имеют следующий геометрический смысл: р является параметром, а е—эксцентриситетом. Вводя в квадрат второе из принятых обозначений и вычитая из первого, найдем:

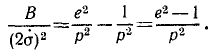
Подставим вместо В в левую часть равенства его значение, принятое в предыдущей задаче:

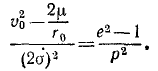
Из этого соотношения определим квадрат эксцентриситета:

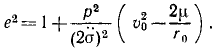
В аналитической геометрии показано, что у эллипса эксцентриситет меньше единицы, у параболы равен единице и у гиперболы больше единицы. Как видно из написанного равенства, эксцентриситет меньше единицы, равен единице или больше единицы в зависимости от того, является ли выражение, стоящее в скобках, отрицательным, нулем или положительным.
Ответ. Эллипс:

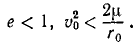
Парабола:

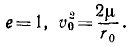
Гипербола:

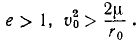
Задача №4

Тело брошено с поверхности Земли вверх по вертикальной линии с начальной скоростью υ₀. Определить величину H поднятия тела, принимая во внимание, что сила притяжения изменяется обратно пропорционально квадрату расстояния от центра Земли; сопротивлением воздуха пренебрегаем. Радиус Земли R = 6370 км, υ₀=1 км/сек.

Решение. Рассматриваем движение тела в поле тяготения Земли. На тело действует одна лишь сила 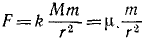, где 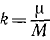— коэффициент пропорциональности, M — масса Земли и m— масса тела.

Коэффициент μ=gR² для силы земного притяжения определен в задаче № 155.

Начальная кинетическая энергия тела 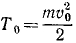 , конечная Т=0; начальная  потенциальная энергия

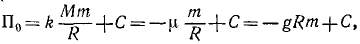
конечная

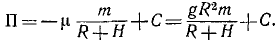
Приравняем сумму энергий в начале движения сумме энергий в конце движения:

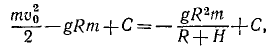
откуда находим 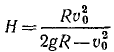 и, подставляя числовые значения, получаем ответ.
Ответ. H = 51 км.

При движении тела в поле тяжести вблизи земной поверхности на тело, кроме силы тяжести, действуют различные диссипативные силы, например сила сопротивления воздуха, поэтому закон сохранения механической энергии здесь неприменим: происходит рассеяние механической энергии, переход ее в другие немеханические виды. Вместе с тем и немеханические виды энергии могут переходить в механическую энергию. Переход не только механической, но и всякой другой энергии из данного вида в эквивалентное количество энергии всякого другого вида подчинен всеобщему закону сохранения и превращения энергии, изучаемому в курсах физики. Согласно этому закону во всякой изолированной системе сумма энергий всех видов (кинетической, потенциальной, тепловой, электрической и т. д.) остается постоянной.

Открытие закона сохранения механической энергии (выражаясь точнее, вывод равенства 246) обычно приписывают Гельмгольцу. Но он провел разработку лишь математической стороны вопроса, однако физическая сущность равенств (246) и (247) не могла получить правильного освещения в трудах Гельмгольца, понимавшего движение не как внутренне присущий материи атрибут, а как нечто внешнее по отношению к материи, «существо которой», по выражению Гельмгольца, «в самом себе представляется для нас покоящимся и бездейственным».

Открытие же всеобщего закона сохранения и превращения энергии приписывают обычно Р. Майеру или Джоулю. Но никакое крупнейшее открытие не может принадлежать одному человеку. В частности, открытие этого закона было подготовлено трудами Декарта, Гюйгенса, Лейбница, Ломоносова, Сади Карно и многих других ученых. Постановка этой проблемы и, в частности, изучение перехода тепловой энергии в механическую было вызвано в первой половине XIX в. развитием промышленности и применением паровых машин, практически осуществляющих этот переход.

Потенциальная энергия механической системы зависит только от положения точек системы в потенциальном поле

Потенциальная энергия системы

Чтобы лучше осветить физическую сторону вопроса, мы все формулы и формулировки в этой главе дали для реальной материальной частицы. Они останутся, конечно, без изменения, если материальную частицу мы заменим материальной точкой, являющейся абстрактным образом материального тела. Они применимы и к такой материальной системе, в которой сумма работ всех сил, приложенных к точкам системы, при перемещении системы из одного положения в другое не зависит от траекторий точек. В частности, они применимы к абсолютно твердому телу, так как работа внутренних сил твердого тела равна нулю.

Очевидно, что потенциальная энергия системы, математически выражается функцией координат всех точек системы

П = П (x₁, y_l, z_l, ..., x_n, у_n, z_n),

причем полный дифференциал этой функции, взятый с обратным знаком, равен сумме элементарных работ сил потенциального поля, приложенных к точкам системы. Такое поле является консервативным, т. е. при движении системы в таком поле под действием только сил этого поля сумма кинетической и потенциальной энергий системы сохраняет постоянное значение.

Равновесные положения механической системы в потенциальном поле, при которых потенциальная энергия системы достигает минимума, устойчивы

Теорема Лежен Дирихле

Отметим интересные свойства равновесия механических систем в потенциальном поле:

1. если система находится в покое в потенциальном поле и занимает положение, при котором потенциальная энергия П минимальна (а следовательно, силовая функция U имеет максимум), то система находится в устойчивом равновесии, т. е., будучи незначительно выведена из этого положении, она стремится вернуться к нему, совершая около него малые колебания;
2. наоборот, если потенциальная энергия при равновесии системы имеет максимум, то система находится в состоянии неустойчивого равновесия и, будучи выведена из этого состояния, не может остаться близкой к первоначальному положению равновесия.

Так, например, на рис. 223, а и б изображен физический маятник в состоянии равновесия, но в положении, изображенном на рис. 223, а, потенциальная энергия маятника минимальна и равновесие устойчиво, а на рис. 223, б потенциальная энергия максимальна и равновесие неустойчиво. Такой маятник является механической системой с одной степенью свободы. Колебания CiicreM со многими степенями свободы складываются из простых колебаний около положения устойчивого равновесия. Указанный Лагранжем метод изучения колебаний (см. § 52) имеет громадное применение в различных отраслях науки и техники и, в частности, в теории вибрации машин.

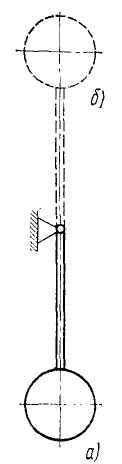
Рис. 223