
Сложение двух сил в теоретической механике - задачи с решением
Сложение двух сил:
Сложение двух сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке, производится по тем же двум правилам — правилу параллелограмма и правилу треугольника и теми же методами —графическим, графо-аналитическим и аналитическим (методом проекций).
* Как известно, 1 кГ — сила, с которой 1 кг (килограмм массы) притягивается к земле на широте 45° и на уровне моря.
При сложении сил необходимо учитывать следующее обстоятельство.
В теоретической механике —в механике твердого тела сила — скользящий вектор, т. е. при решении задач силу можно переносить вдоль линии ее действия в любую точку. Поэтому, если на тело действуют как, например, две силы 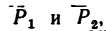
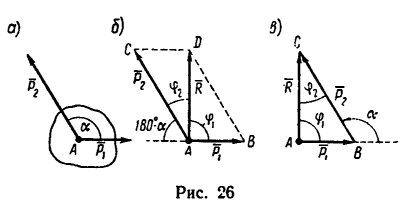
Задача:
Определить равнодействующую 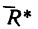 двух сил
двух сил 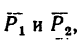 модули которых соответственно равны
модули которых соответственно равны 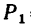 = 40 я и
= 40 я и 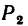 = 80 н; сила
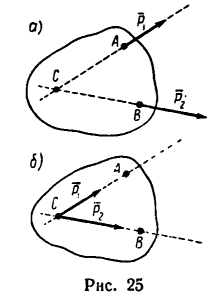
= 80 н; сила 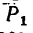 направлена горизонтально вправо, а Р2 образует с Р, угол а = 120’ (рис. 26, а).
направлена горизонтально вправо, а Р2 образует с Р, угол а = 120’ (рис. 26, а).
Задачу можно решить графическим или графо-аналитическим методом, используя в обоих случаях либо правило параллелограмма, либо правило треугольника (см. задачи 1-1 и 11-3).
Графическим методом рекомендуем решить задачу самостоятельно, а здесь приведем графо-аналитические решения по обоим правилам.
Решение 1-по правилу параллелограмма:
1. Используя условие задачи и приблизительно соблюдая масштаб, изображаем параллелограмм ABCD (рис. 26,6). Порядок построения такой: из точки А проводим отрезок 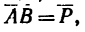 затем из той же точки А под углом 120° к отрезку АВ проводим отрезок
затем из той же точки А под углом 120° к отрезку АВ проводим отрезок 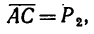 из точек В и С проводим прямые BD || АС и CD || АВ и, наконец, проводим диагональ
из точек В и С проводим прямые BD || АС и CD || АВ и, наконец, проводим диагональ 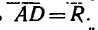
2. Используя формулу (1), можем найти модуль равнодействующей:
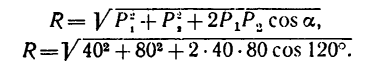
------------------------------------------------
* Необходимо помнить, что если в задаче требуется найти какой-либо вектор (в данной задаче R), то это значит, нужно найти модуль вектора и его направление
------------------------------------------------
Имея в виду, что cos 120°= — sin 30°= —0,5, получаем
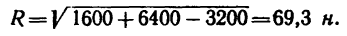
3. Применяя к A ABD (или к Л ACD) (см. рис. 26,6) теорему синусов, получаем откуда
и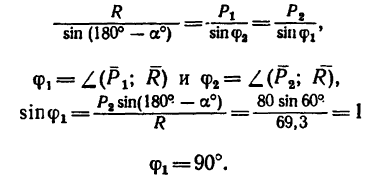
Таким образом, вектор равнодействующей 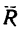 перпендикулярен к силе
перпендикулярен к силе 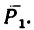
Угол 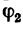 можно найти либо как разность
можно найти либо как разность
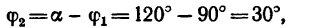
либо из теоремы синусов:
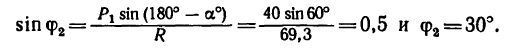
Один и тот же результат, полученный различными путями, подтверждает правильность решения задачи.
Ответ. Равнодействующая данных сил равна 69,3 к, и линия ее действия образует с направлением силы 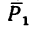 прямой угол.
прямой угол.
Решение 2-по правилу треугольника.
1. Используя условие задачи, строим треугольник сил АВС (рис._26,в). Порядок построения такой: из точки А проведем отрезок 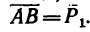 Затем из уточки В под углом а =120° к направлению
Затем из уточки В под углом а =120° к направлению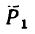 проводим отрезок
проводим отрезок 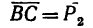 и, наконец, «замкнем» треугольник отрезком АС, который изобразит искомую равнодействующую R.
и, наконец, «замкнем» треугольник отрезком АС, который изобразит искомую равнодействующую R.
В получившемся треугольнике 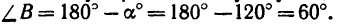
2. Применяем к треугольнику АВС известную из тригонометрии теорему косинусов:
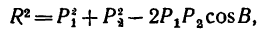
откуда модуль равнодействующей
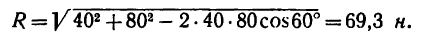
3. Углы 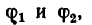 определяющие направление равнодействующей относительно заданных сил, находим, как и в первом решении, по теореме синусов.
определяющие направление равнодействующей относительно заданных сил, находим, как и в первом решении, по теореме синусов.
Необходимо заметить, что в задаче складываются одинаковые по модулю силы, но угол, образуемый их направлениями, уменьшается, и это приводит к увеличению модуля равнодействующей и к уменьшению угла 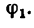
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |