Равновесие трех непараллельных сил в теоретической механике

Равновесие трех непараллельных сил:

При решении задач определенное практическое значение имеет теорема о равновесии трех непараллельных сил: если три непараллельные силы образуют уравновешенную систему, то линии их действия пересекаются в одной точке *.

Эта теорема используется для решения задач в тех случаях, когда на тело действует уравновешенная система трех сил, причем одна сила задана по модулю и направлению, для другой известно лишь направление, а у третьей — неизвестны ни модуль, ни направление.

Приведем решение двух задач этого типа.

Задача №1

Балка АВ поддерживается в горизонтальном положении стержнем CD, наклоненным к балке под углом а = 40°; крепления в точках А, С и D шарнирные (рис. 59, а). Определить реакцию шарнира А и усилие, растягивающее стержень CD, если на конце В балки действует вертикальная сила, равная 20 кн. Весом балки и стержня пренебречь.

Решение — графо-аналитическим методом.

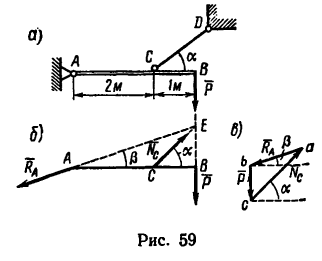
1.    На балку действуют три силы (см. рис. 59, а): известная нагрузка Р уравновешивается двумя реакциями: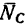

Построим расчетную схему (рис. 59, б). Отрезок АВ изображает данную балку. На точку В действует вертикальная нагрузка 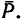В точке С под углом а = 40° на балку действует реакция 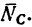Направления действия сил 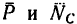известны, значит можно получить точку Е, в которой пересекаются их линии действия.

В соответствии с теоремой о равновесии трех непараллельных сил через точку Е пройдет и линия действия реакции 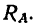. Значит 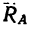действует вдоль линии ЕА, направленной под углом 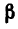к АВ.

2.    Силы 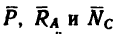образуют уравновешенную систему. Следовательно, силовой треугольник, построенный из векторов этих сил, должен быть замкнут. Строим треугольник bас (рис. 59, в), в котором отрезок bс изображает силу 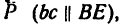отрезок са — силу 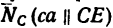и отрезок ab—силу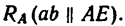

3.    Модули сил 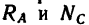можно определить по теореме синусов, но предварительно необходимо определить углы треугольника abc:

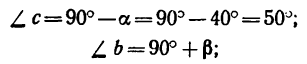
но угол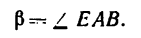

Из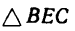

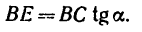
Теперь из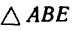

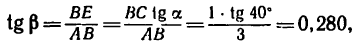
откуда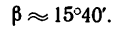

Таким образом,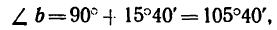

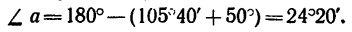
4.    По теореме синусов

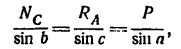
отсюда

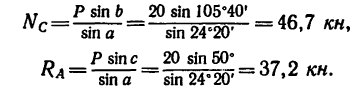
Таким образом, усилие в стержне CD равно его реакции 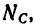т. е. 46,7 кн, реакция шарнира А образует с балкой АВ угол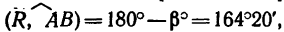а ее модуль 37,2 кн.

Задача №2

Горизонтальная балка, имеющая в точке А шарнирно-неподвижную опору, а в точке В —шарнирно подвижную с опорной плоскостью, наклоненной под углом а=30° к горизонтали, нагружена в точке С вертикальной силой Р = 50 кн (рис. 60, а). Определить реакции опор.

Решение —методом проекции.

1.    Кроме нагрузки 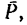на балку действуют реакции двух шарнирных опор. Направление реакции шарнирно-подвижной опоры известно —оно образует с опорной плоскостью катка прямой угол. Значит 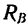— реакция шарнира В, перпендикулярная к опорной плоскости катка, будет образовывать с балкой ВА угол, равный (90—а)°.

Покажем силы Р и 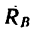на расчетной схеме (рис. 60, б). Так как направление этих сил известно, то точку пересечения их линий действия легко зафиксировать (точка D). Прямая AD определяет теперь направление реакции  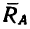неподвижного шарнира (теорема о равновесии трех непараллельных сил).

2.    Найдем угол 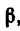 образуемый RA с балкой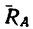

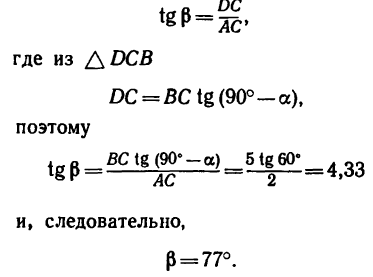
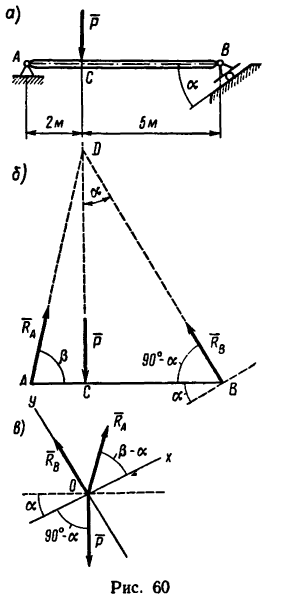
3.    Так как силы 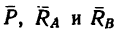образуют уравновешенную систему сходящихся сил, для удобства дальнейшего решения изобразим их отдельно, приложенными к произвольной точке О (рис. 60, в), и расположим оси так, чтобы ось х была перпендикулярна к 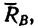а ось у совпадала с этой силой (штриховая    горизонтальная линия    Рис. 60 проведена на рис. 60, в для лучшей ориентировки при определении углов, образуемых силами 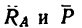с осями).

4.    Составим уравнения равновесия: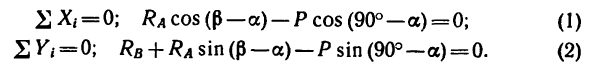

5.    Из уравнения (1)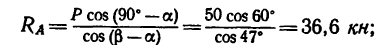

из уравнения (2)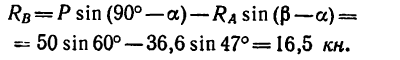

Реакция подвижного шарнира 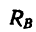= 16,5 кн, реакция неподвижного шарнира 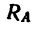= 36,6 кн\ она наклонена к балке под углом  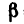= 77°.

Как видно, и при графо-аналитическом методе и при методе проекций применение теоремы о равновесии трех непараллельных сил приводит к довольно длинному решению задачи. Эту теорему для решения задачи выгодно применять, лишь используя графический метод решения.

Если рис. 59, б и 60, б выполнить в масштабе, то из этого построения определяется направление (угол 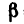) реакции шарнира А.

Затем, построив в масштабе силовой треугольник, найдем модули обеих неизвестных реакций.