Равновесие пространственной системы сходящихся сил в теоретической механике

Пространственная система сил:

При решении задач, приведенных в этой главе, необходимо использовать не две оси координат, которые всегда можно расположить в одной плоскости —в плоскости рисунка, иллюстрирующего задачу, а три взаимно перпендикулярные оси.

Эти оси нельзя расположить в одной плоскости и при изображении пространственной системы сил на рисунке надо использовать одну из принятых в машиностроительном черчении аксонометриейческих проекций (ГОСТ 2.305—68. Изображения — виды, разрезы, сечения).

На рис. 145 показано изображение трех взаимно перпендикулярных плоскостей в изометрической проекции. Пересечение двух вертикальных плоскостей определяет положение вертикальной оси z,

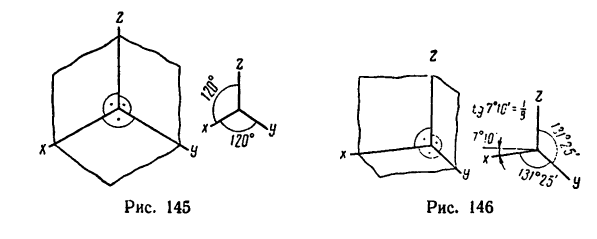
пересечением обеих вертикальных плоскостей с горизонтальной определяются положения двух горизонтальных осей х и у.

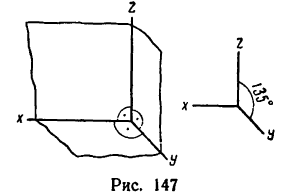
На рис. 146 представлены те же три взаимно перпендикулярные плоскости в диметрической проекции, а на рис. 147—в фронтальной диметрической проекции. На каждом рисунке справа показано положение осей при изображении соответствующей проекции.

Если при решении задач, в которых рассматривается пространственная система сил, трудно представить взаимное расположение сил или их расположение относительно выбранных осей координат, то следует изготовить из плотной бумаги модель трех пересекающихся под прямым углом плоскостей, а линии пересечения плоскостей выделить цветными линиями и обозначить их соответственно х, у и z, В такой модели трех взаимно перпендикулярных осей можно помещать модели систем сил, рассматриваемых в задаче, изготовленные из пластилина, проволочек и спичек.
 

Правило параллелепипеда сил

Простейшую пространственную систему сходящихся сил образуют три силы, приложенные к одной точке.

Для сложения таких трех сил применяется правило параллелепипеда (рис. 148). Если даны силы 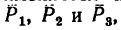то заменяющая их действие равнодействующая Р по модулю и направлению соответствует диагонали АЕ параллелепипеда, ребра которого АВ, АС и AD соответствуют трем силам.

В частном случае, который наиболее характерен для решения практических задач, три данные силы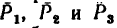 взаимно перпендикулярны и тогда при их сложении образуется прямоугольный параллелепипед (рис. 149).

В этом случае модуль равнодействующей

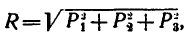
а направление R относительно каждой из составляющих сил можно найти по формулам

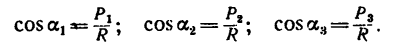
Так же как и правило параллелограмма (см. § 1-1, 5-2 и 6-2), правило параллелепипеда можно использовать не только при сложении сил, но и при разложении данной силы на три составляющие. Наиболее часто производят разложение силы на составляющие, действующие по трем взаимно перпендикулярным направлениям.

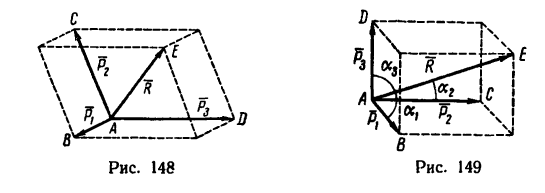
Задача №

Три цепи одинаковой длины l соединены вместе кольцом А (рис. 150, о). Оставшиеся свободными концы цепей закреплены в трех точках В, С и D таким образом, что эти точки образуют вершины куба. Как необходимо установить под кольцо А подпорку АЕ и какую длину она должна иметь, чтобы кольцо А располагалось относительно точек В, С и D как четвертая вершина куба? При этом цепь АВ должна быть натянута силой Р, а цепи AD и ИС—силами 2Р каждая. Определить также усилие в подпорке АЕ. Весом подпорки пренебречь.

Решение.

1.    Из точки А (рис. 150, б) вдоль цепей отложим заданные силы: вдоль цепи АВ — силу Р, вдоль цепей АС и AD — силы 2Р. Построив на них параллелепипед, получим в нем диагональ ААХ, выражающую равнодействующую трех усилий в цепях.

Вдоль линии действия равнодействующей R нужно установить подпорку АЕ, которая должна соответствовать диагонали параллелепипеда подобного силовому параллелепипеду.

2.    Находим модуль равнодействующей:

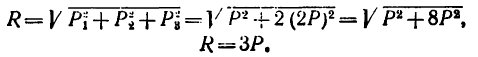
3.    Из подобия двух показанных на рис. 150, б параллелепипедов следует пропорция

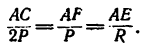
Зная, что длина цепи АС — 1, находим длину подпорки АЕ: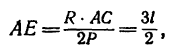

а также расстояние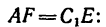

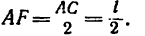
Таким образом, усилие в подпорке равно 3Р, длина подпорки 1,5l, а установить ее нужно так, чтобы нижний конец Е находился

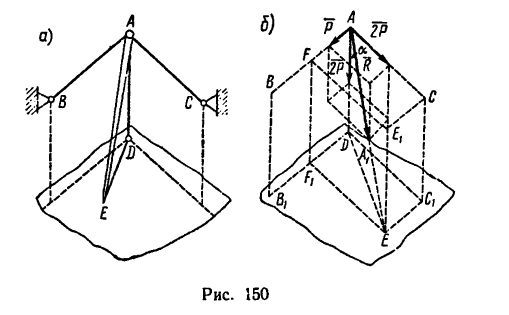
от 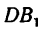на расстоянии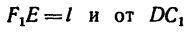—на расстоянии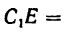
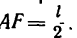
Решение этой задачи после выполнения пункта 2 можно продолжать иным путем. Можно найти угол а, образуемый 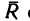с вертикальной цепью, а затем определить из ADE длину АЕ и т. д.

Задача №

Найти усилия в стержне АВ и цепях АС и AD, поддерживающих груз Q весом 42 кГ, если AВ = 145сл, AС=80сл, AD = 60 см. Плоскость прямоугольника CADE горизонтальна, а плоскости V п W вертикальны. Крепление в точке В шарнирное (рис. 151, а).

Решение.

1.    Разложим силу Q на три составляющие 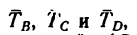направленные соответственно вдоль стержня АВ и ценен АС и АО. Для этого, приняв вектор Q за диагональ 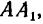построим силовой параллелепипед, из которого видно, что составляющая 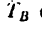сжимает

стержень АВ, а составляющие 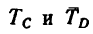растягивают цепи АС и AD (рис. 151, б).

2.    Соответственно приняв отрезок BE за диагональ, а стержень АВ и цепи АС и AD—за ребра, построим параллелепипед, подобный силовому (см. рис. 151, б).

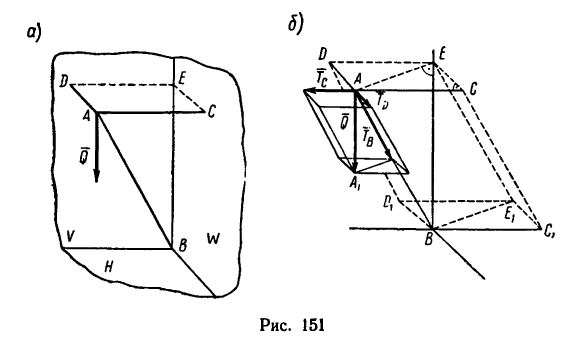
3.    Из подобия параллелепипедов, полученных на рис. 151, б, следует пропорция

;

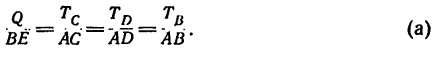4.    Длины трех отрезков из четырех, входящих в пропорцию, известны. Длина отрезка BE неизвестна. Найдем ее из рассмотрения прямоугольных треугольников АВЕ и АСЕ:

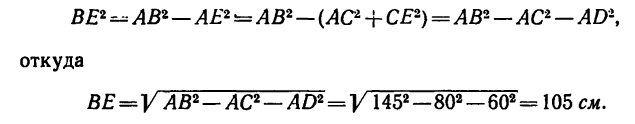
5.    Рассматривая теперь первое отношение пропорции (а) вместе со вторым, а затем с третьим и четвертым, находим

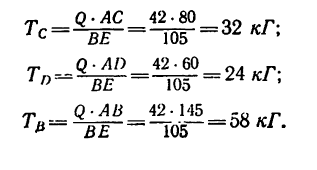
Проекция силы на три взаимно перпендикулярные оси. Определение равнодействующей системы пространственных сил, приложенных к точке

Если требуется определить проекции силы 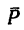на три взаимно перпендикулярные оси (рис. 152), то обычно силу проектируют сначала на одну из плоскостей (например, горизонтальную), а уже затем на оси, расположенные в этой плоскости. При этом нужно обратить внимание на то, что в отличие от проекций силы на оси, являющихся скалярами, проекция силы на плоскость 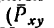на рис. 152) —величина векторная (Е. М. Никитин, § 39).

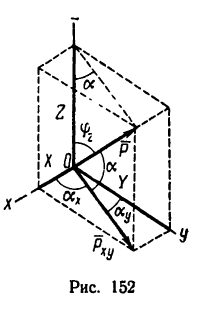
Легко заметить, что на трех взаимно перпендикулярных проекциях можно построить прямоугольный параллелепипед, диагональю которого является проектируемый вектор.

Из рис. 152 видно, что проекция на горизонтальную плоскость

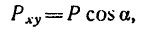
поэтому

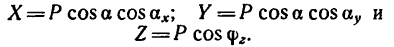
Если же известны углы 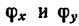(на рисунке они не показаны), образуемые вектором Р с осями х и у, то его проекции на эти оси соответственно равны

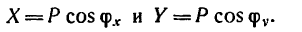
При помощи проекций сил на три оси легко определить равнодействующую системы сил, приложенных к точке.

Для этого необходимо:

1)    выбрать расположение осей так, чтобы проекции всех сил определились простейшим образом;

2)    найти проекции всех сил на каждую из осей;

3) сложить проекции всех сил на каждую из осей и найти таким образом три проекции искомой равнодействующей на оси:

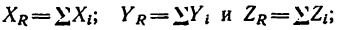
4)    определить модуль равнодействующей Р:

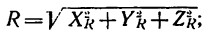
5)    определить направление равнодействующей, найдя какие-либо два угла из трех:

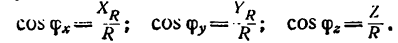
Задача №

На одну из вершин куба действуют пять сил таким образом, что три силы направлены вдоль ребер, сходящихся в этой вершине; четвертая сила направлена по диагонали грани, а пятая—вдоль диагонали самого куба. Определить равнодействующую.

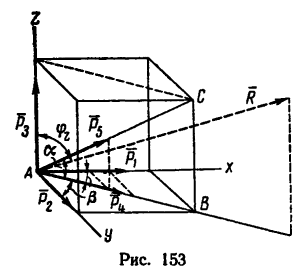
1.    Приняв точку А за вершину куба, изобразим данные силы. Силы 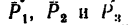действуют вдоль ребер куба; сила Р4 — вдоль диагонали АВ нижней грани и сила 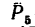— вдоль диагонали AС куба (рис. 153).

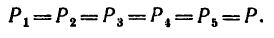
2.    Ось х совместим с ребром куба, вдоль которого действует сила 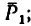ось у—с ребром, вдоль которого действует сила 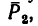и ось z — с третьим ребром.

3.    Найдем проекции сил на каждую из осей:

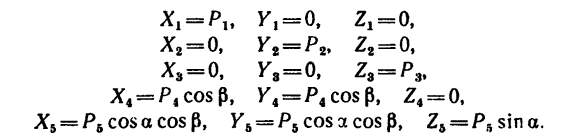
4. Сложим проекции на каждую ось и найдем проекции равнодействующей, учитывая, что модули всех сил равны между собой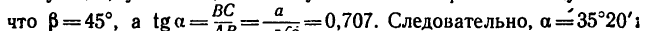

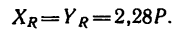
Равенство проекций получается из-за симметричности расположения сил относительно диагональной плоскости куба (плоскости, в которой расположен АВС).

5. Определим модуль равнодействующей: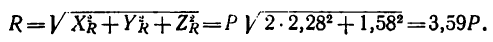

6.    Так как силы расположены симметрично относительно диагональной плоскости куба, линия действия равнодействующей находится в плоскости симметрии расположения сил, проходящей через ось z. Поэтому направление равнодействующей определяется углом 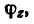образуемым линией действия 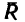с осью z;

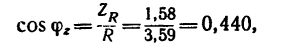
чему соответствует угол

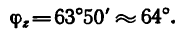
На рис. 153 положение равнодействующей показано штриховым вектором
 

Равновесие пространственной системы сходящихся сил

Если система сходящихся сил уравновешена, то ее равнодействующая R = 0, а это означает, что и проекции равнодействующей на.три взаимно перпендикулярные оси равны нулю 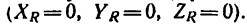Отсюда образуются три уравнения равновесия:

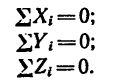
При помощи этих уравнений и решаются задачи на равновесие пространственной системы сходящихся сил.

Уравнений равновесия —три, следовательно, статически определимой является такая пространственная система сходящихся сил, в которой неизвестных сил не более трех.

Задача №

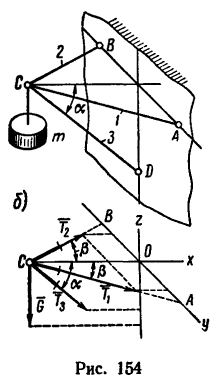
Груз, масса которого m= 500 кГ, подвешен на кронштейне ABCD, состоящем из трех стержней 1,2 и 3. Стержни 1 и 2 образуют в месте соединения прямой угол и расположены в горизонтальной плоскости. Стержень 3 образует с горизонтальной плоскостью угол а = 40° (рис. 154, а). Определить усилия, вызванные действием груза в стержнях. Соединения стержней между собой и с вертикальной стенкой шарнирные. Весом стержней пренебречь.

Решение.

1.    Решаем задачу в единицах системы СИ. На точку С кронштейна действует вертикальная нагрузка, равная весу массы груза, поэтому

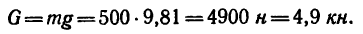
2.    Действие веса G на кронштейн уравновешивается реакциями трех стержней. Известно, что реакции направлены вдоль стержней (так как соединения стержней шарнирные). Нужно определить их модули и направление каждой реакции, т. е. определить, какой из стержней сжат, а какой растянут.

Мысленно разрежем стержни вблизи точки С и изобразим узел С, образуемый соединением трех стержней отдельно (рис. 154, б) вместе с четырьмя действующими на него силами: вертикально вниз действует известная сила G = 4,9 кн, а вдоль стержней действуют три их реакции: 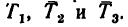Причем условно считаем, что все стержни растянуты, поэтому на рис. 154, б все реакции направлены от узла С.

3.    Расположим оси координат, как показано на рисунке. Замечая, что осью х прямой угол АСВ разделен пополам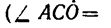 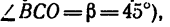составим три уравнения равновесия для пространственной системы сходящихся сил:

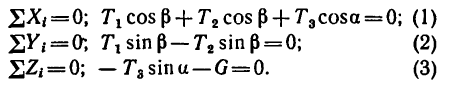
4 Решаем полученную систему уравнений. Из уравнения (3)

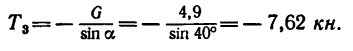
Знак «минус» показывает, что реакция 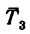направлена в сторону, противоположную той, которая изображена на рисунке. Значит стержень 3 сжат усилием 7,62 кн.

Из уравнения (2)

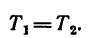
Из уравнения (I)

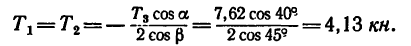
Числовые значения реакций 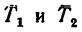получились положительные, значит стержни 1 и 2 растянуты силами по 4,13 кн.

5. Если найденные значения реакций стержней перевести в единицы технической системы, то

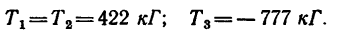
Правильность перевода из единиц системы СИ в единицы технической системы рекомендуется проверить самостоятельно.

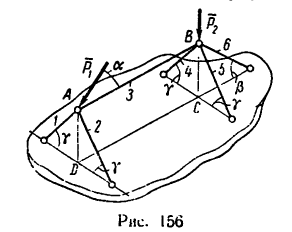
Задача №

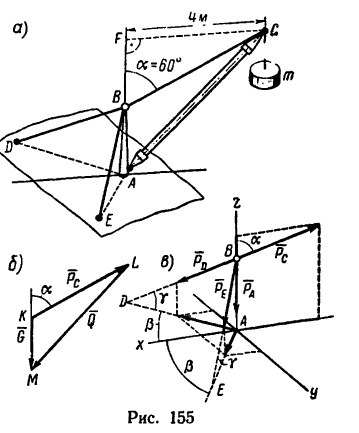
Переносный кран, поднимающий груз массой m = 2000/кг, устроен так, как указано на рис. 155, a; AB = AD = АЕ=2м; угол DAE —120", плоскость АВС, в которой расположена стрела АС крана, делит двугранный угол DAE пополам.

Определить силу, сжимающую вертикальную стойку АВ, и силы, растягивающие тросы BD и BF весом частей крана пренебречь.

Решение.

1.    В задаче рассматривается равновесие системы тел—стрелы и стойки, связанных струной ВС. Прежде чем приступить к определению усилий в стойке и тросах, необходимо найти натяжение струны ВС.

2.    В точке С на кран действует вес 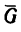груза, масса которого т, следовательно,

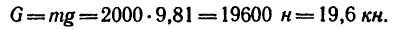
Разложим вес G на две составляющие, действующие вдоль струны ВС и стрелы АС, воспользовавшись правилом треугольника (рис. 155, б). Для этого из произвольной точки К построим вектор G, а затем из его начала и конца проведем линии, параллельные ВС и АС. В получившемся силовом треугольнике KLM (KL || ВС и LM|| СА) сторона KL изображает силу 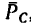растягивающую струну ВС, а сторона LM — силу 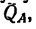сжимающую стрелу АС.

Из построения следует, что

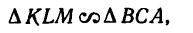
поэтому

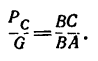
Отсюда

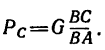
Не известную по условию задачи длину струны ВС легко найти, рассмотрев прямоугольный треугольник BCF (см. рис. 155, а)

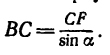
Таким образом,

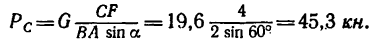
3.    Перенесем силу 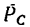вдоль линии ее действия из точки С в точку В и рассмотрим равновесие узла В. на который, кроме нагрузки 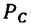=45,3к:н, действуют реакции трех связей: 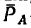—реакция стойки, 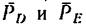— реакции тросов BD и BE. В соответствии с общим правилом считаем, что все связи растянуты (рис. 155, в).

4.    Расположим систему координатных осей, как показано на рис. 155, в и составим три уравнения равновесия:

)

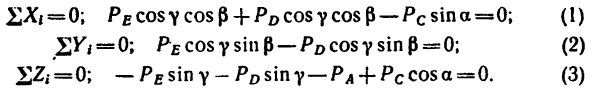Замечая, что y = 45° (так как треугольники ВАЕ и BAD имеют равные катеты: BA=AE — AD) и а = 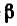= 60° (так как угол DAE, равный 120°, осью х разделен пополам), решаем получившиеся уравнения.

Из уравнения (2)

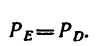
Теперь уравнения (1) и (3) примут такой вид:

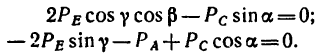
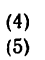
Умножим обе части уравнения (5) на cos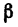 и сложим его после этого с уравнением (4):

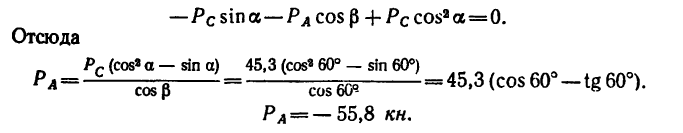
Знак «минус» указывает на то, что реакция 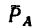направлена не от узла В, а к узлу, т. е. стойка сжата силой 55,8 кн.

Подставив найденное значение 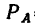= — 55,8 кн в уравнение (5), найдем реакции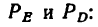
Отсюда

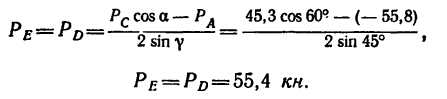
Тросы AD и AE растянуты усилиями по 55,4 кн.

Следующую задачу рекомендуется решить самостоятельно.

Момент силы относительно оси

Чтобы определить момент силы 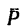относительно заданной или выбранной оси, например оси z (рис. 157), необходимо выполнить следующие операции:

• 1)    расположить плоскость Н перпендикулярно оси z;
• 2)    определить проекцию силы Р на плоскость H — найти
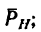
• 3)    из точки пересечения о.си с плоскостью (из точки О) провести перпендикуляр к направлению проекции 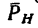этого перпендикуляра О А — плечо силы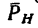
• 4)    определить знак момента, придерживаясь такого правила: посмотрим на плоскость H со стороны положительного направления оси, если увидим, что проекция 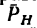поворачивает плечо против хода часовой стрелки, значит момент имеет положительный знак; а если проекция 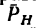поворачивает плечо по часовой стрелке (как это показано, например, на рис. 157), момент имеет отрицательный знак;
• 5)    находим числовое значение момента силы Р относительно оси; для этого 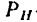—модуль проекции силы Р на плоскость, перпендикулярную к оси, умножаем на плечо О А.

Таким образом (см. рис. 157)

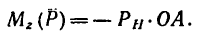
Момент силы относительно оси, так же как и момент силы относительно точки, измеряется по Международной системе (СИ) в ньютон-метрах (н м) или в килоньютон-метрах (н-м), а по технической системе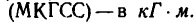

Для успешного решения задач и облегчения составления уравнений моментов относительно осей нужно иметь в виду три частных случая, в которых момент силы относительно оси равен нулю (рис. 158):

Случай 1-й (рис. 158, а). Сила Р или линия ее действия пересекает ось; в этом случае плечо О А — 0, поэтому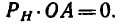

Случай 2-й (рис. 158, б). Линия действия силы параллельна оси; в этом случае — 0, поэтому

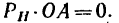
Случай 3-й (рис. 158, в). Линия действия силы Р совпадает с осью; в этом случае и 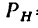=0 и плечо 0А= 0.

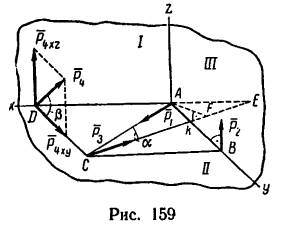
Задача №

К вершинам квадрата ABCD (AB = AD = 2 м), расположенного в горизонтальной плоскости, приложены силы как показано на рис. 159. Сила 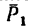направлена по диагонали АС сила 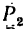действует вверх перпендикулярно к плоскости квадрата; сила 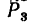действует в плоскости квадрата, и ее направление образует с диагональю С А угол а = 20°; сила 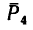действует в плоскости, перпендикулярной к плоскости квадрата, и направлена к стороне DC под углом = 30°. Определить моменты каждой силы относительно осей х, у и z.

Модули сил

Решение:

1.    Замечаем, что расположение осей, показанное на рис. 159, определяет положение трех взаимно перпендикулярных плоскостей; плоскости , перпендикулярной к оси у, плоскости II, перпендикулярной к оси г, и плоскости III, перпендикулярной к оси х.

2.    Определяем моменты силы 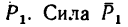приложена в точке А пересечения всех трех осей, следовательно, согласно первому частному случаю (см. рис. 158, а),

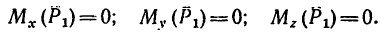
3.    Определяем моменты силы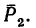

Сила 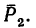приложенная в точке В, пересекает ось у и параллельна оси z. Следовательно, согласно первому и второму частным случаям (см. рис. 158, в)

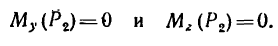
Чтобы определить момент силы 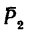относительно оси х, необходимо найти проекцию 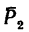на плоскость III, перпендикулярную к оси х. Сила 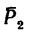расположена в этой плоскости и, следовательно, проектируется полностью 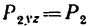Плечом является сторона АВ квадрата. Знак момента положительный, так как если посмотреть от точки D вдоль оси х на плоскость III, то увидим, что сила 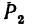поворачивает плечо АВ против хода часовой стрелки. Поэтому

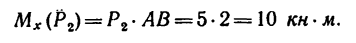
4.    Определяем моменты силы

Сила 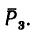расположена в горизонтальной плоскости. В этой же плоскости расположены оси х и у. Поэтому линия действия силы 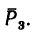пересекает ось х (в точке Е) и ось у (в точке К)- Значит

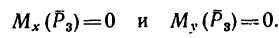
Плоскость, в которой расположена сила 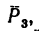перпендикулярна оси z, значит 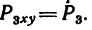Плечо AF силы 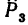найдем из треугольника AFC:

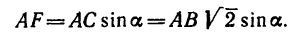
Знак момента положительный (если посмотреть на плоскость II со стороны оси z). Поэтому

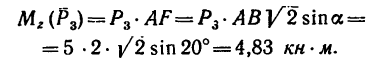
5.    Определяем моменты силы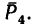

Линия действия силы 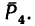пересекает ось х, следовательно,

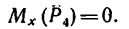
Спроектируем силы 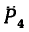на плоскости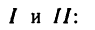

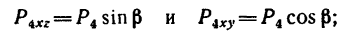
плечом силы 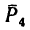является сторона квадрата AD.

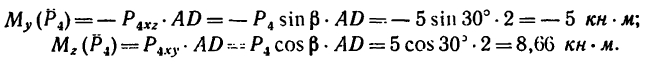
Равновесие произвольной пространственной системы сил

Произвольную пространственную систему сил, так же как и плоскую, можно привести к одной точке и заменить главным вектором 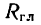и главным моментом 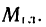Только в этом случае линия действия главного вектора может находиться не в плоскости действия главного момента.

Если 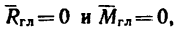то система сил уравновешена и отсюда образуется система шести уравнений равновесия:

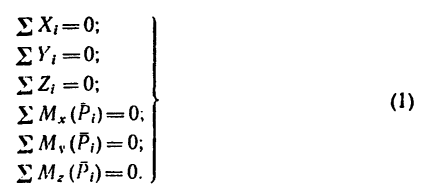
Первые три уравнения (уравнения проекций) получены из условия 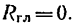Если главный вектор равен нулю, то и алгебраические суммы проекций всех сил на каждую из осей также равны нулю.

Последние три уравнения (уравнения моментов) получены из условия 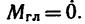Если главный момент системы сил равен нулю, то алгебраические суммы моментов сил относительно каждой из осей равны нулю.

Для облегчения составления уравнений равновесия тело, равновесие которого рассматривается, целесообразно изображать вместе с действующими на него силами в проекциях на три основные

плоскости, т. е. изображать вид спереди, вид сверху и один боковой вид —вид слева или вид справа (см. задачи 115-22, 116-22 и 117-22).

В частном случае линии действия сил, образующих пространственную систему, могут оказаться параллельными. Тогда одну из осей (например, ось z) выгодно расположить параллельно силам (рис. 160), а две другие оси расположатся в плоскости, перпендикулярной к линиям действия сил.

Легко понять, что для уравновешенной пространственной системы параллельных сил вместо шести уравнений можно составить лишь три: алгебраическую сумму проекций сил на ось, параллельную данным силам, и два уравнения моментов относительно двух других осей. Остальные уравнения превратятся в тождество вида 0 = 0.

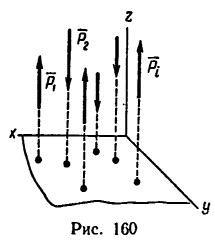
В соответствии с расположением осей (см. рис. 160) уравнения равновесия имеют вид:

Для пространственной системы параллельных сил можно составить лишь три уравнения равновесия, поэтому, чтобы задача была статически определимой, в ней должно содержаться не более трех неизвестных сил.

Задача 114-22. На рис. 161 схематично изображена трехколесная платформа для перевозки грузов. На платформе лежит груз Р = 8кн таким образом, что его вес можно считать приложенным в точке D, причем EO = DF = 0,1 м и DE = OF = 0,5 м.

Определить силы давления, производимые колесами на горизонтальную опорную плоскость.

Собственным весом платформы пренебречь.

Решение.

1.    Давления, производимые колесами, численно равны реакциям опоры, поэтому приложим к каждому колесу перпендикулярно к опорной плоскости реакции Образовалась система четырех параллельных сил, расположенных в пространстве.

2.    Расположим оси координат, как показано на рис. 161, и составим уравнения равновесия:

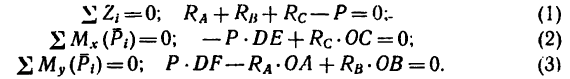
3.    Решаем полученную систему уравнений. Из уравнения (2)

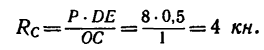
Затем решение можно продолжить так. Подставляя известные числовые значения в уравнения (1) и (3) и перенеся известные члены в правую сторону, получаем такую систему двух уравнений:

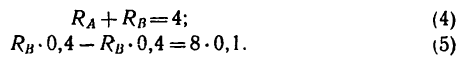
Разделим обе части уравнения (5) на 0,4, тогда система уравнений приобретает такой простой вид:

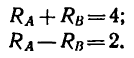
Сложив эти уравнения, найдем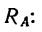

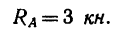
Вычтем из первого второе, найдем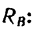

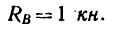
Как видно, реакции не равны между собой, следовательно, соответственно колеса давят на опорную плоскость также неодинаково.

Как нужно поместить груз Р, чтобы силы давления, производимые колесами, равнялись между собой?

В следующих задачах рассматриваются системы сил, произвольно расположенные в пространстве.

Задача №

Квадратная крышка весом 400 н удерживается приоткрытой на 60э над горизонтальной плоскостью противовесом Q (рис. 162). Определить, пренебрегая трением на блоке D,

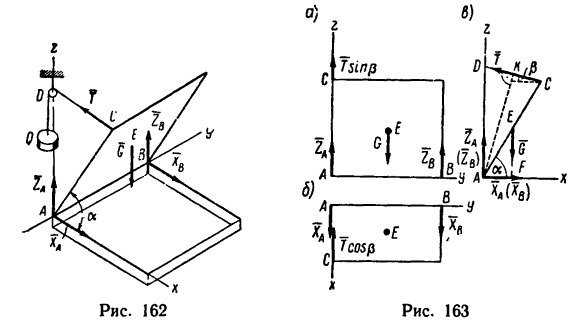
вес противовеса Q и реакции шарниров А и В, если блок D укреплен на одной вертикали с шарниром А и AD=AC.

Решение.

1.    Выбрав за начало координат точку А и расположив оси так, как показано на рис. 162, покажем на этом же рисунке активные силы и реакции опор.

На крышку действует сила тяжести G, которую считаем приложенной в точке Е (центр симметрии квадрата), и реакция 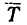нити CD, приложенная в точке С. Сила Т численно равна весу Q противовеса. Действие этих сил уравновешивается реакциями шарниров А и В. Так как силы действуют в плоскостях, перпендикулярных к оси у, то реакции шарниров лежат в плоскостях, перпендикулярных к той же оси. Поэтому реакцию шарнира А заменим двумя составляющими, а реакцию шарнира В — составляющими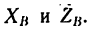

2.    Если составление уравнений равновесия по рис. 162 затруднительно, можно предварительно изобразить крышку вместе с действующими на нее силами в трех проекциях, как это сделано на рис. 163:

а)    вид спереди, ось х перпендикулярна к плоскости проекции;

б)    вид сверху, ось г перпендикулярна к плоскости проекции;

в)    вид слева, ось у перпендикулярна к плоскости проекции.

3.    Составим уравнения равновесия.

Для составления уравнений проекций на ось х воспользуемся рис. 163, б или 163, в:

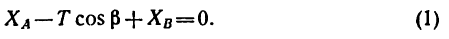
На ось у силы не проектируются, так как все они перпендикулярны к этой оси.

Для составления уравнений проекций на ось z воспользуемся рис. 163, а или 163, в:

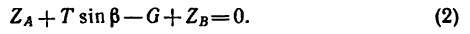
Для составления уравнения моментов относительно оси х воспользуемся рис. 163, а:

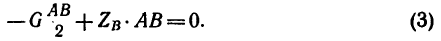
Для составления уравнения моментов относительно оси у воспользуемся рис. 163, в:

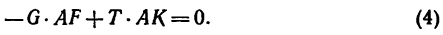
Для составления уравнения моментов относительно оси г воспользуемся рис. 163, б:

4.    Решаем полученные уравнения.

Из уравнения (5) находим (так как ):
Из уравнения (4)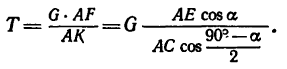
Так как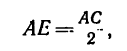
то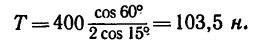 

Из уравнения (3)

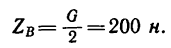
Из уравнения (2)

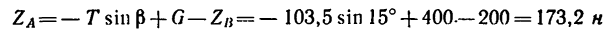
(угол 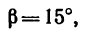так как треугольник ACD равнобедренный).

Из уравнения (1)

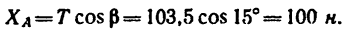
Таким образом, чтобы крышка находилась в равновесии приоткрытой под углом 60°, вес противовеса должен быть Q = T = 103,5 н. При этом реакция шарнира А имеет две составляющие: горизонтальную 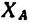= 100 н и вертикальную 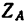=173,2 н, а реакция шарнира В направлена вертикально и равна 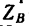= 200 и.

Задача №

На вал 1 ворота намотана веревка, удерживающая груз Q (рис. 164). Радиус колеса 2 ворота в четыре раза больше радиуса вала. Веревка, прикрепленная к ободу колеса и натягиваемая грузом силой Р =80 н, сходит с колеса в точке F по касательной; радиус DF колеса образует с вертикалью угол а=60и. Определить величину груза Q, при котором ворот остается в равновесии, а также реакции подшипников А и В, если общий вес вала и колеса G = 600 н и приложен в точке С (АС = 0,4 м).

Решение.

1.    Три нагрузки-вес и грузы , приложенные к вороту, уравновешиваются реакциями подшипников Л и В. Нагрузки

действуют в плоскостях, перпендикулярных к оси вала, и, следовательно, не смещают вал вдоль оси, поэтому и реакции подшипников расположатся в плоскостях, перпендикулярных к этой же оси. Заменим их составляющими 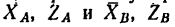(рис. 164).

Следует учесть, что обычный подшипник не создает реакции, направленной вдоль оси вала. Нели на вал действуют нагрузки, смещающие вал вдоль оси, то один из подшипников должен быть заменен подпятником.

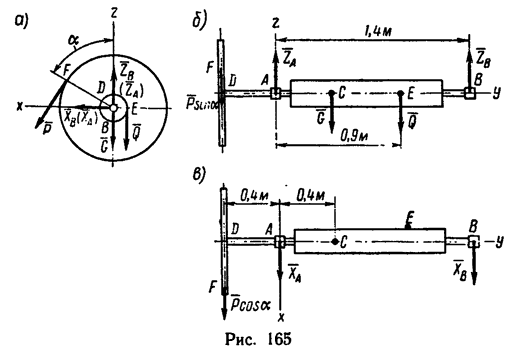
2.    Изобразим ворот со всеми действующими на него силами в трех проекциях (рис. 165 а, б, в) и при помощи их составим уравнения равновесия.

Так же как и в предыдущей задаче, уравнение проекций на ось у превратится в тождество вида 0 = 0. При составлении уравнения моментов относительно оси у- уравнения (4)—нужно учитывать, что радиус колеса R в четыре раза больше радиуса вала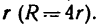
3. Из уравнения (5)

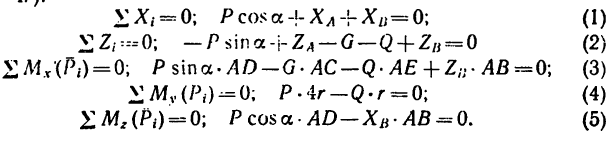
3. Из уравнения (5)

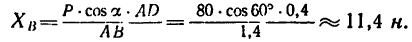
Из уравнении (4)

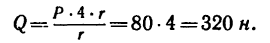
Из уравнения (3)

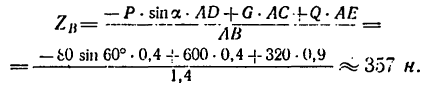
Из уравнения (2)

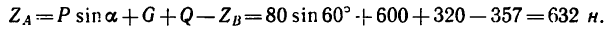
Из уравнения (1)

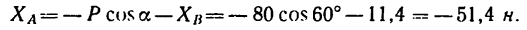
Задача 117-22. Деревянный брус прямоугольного поперечного сечения b= 20 см и h= 25 см жестко заделан в стене таким образом, что выступающая из стены часть бруса горизонтальна и имеет длину (см. рис. 165, о). Свободный конец бруса нагружен тремя силами: силон 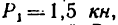, действующей вдоль вертикального ребра торца бруса, силой 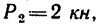приложенной в центре тяжести торца и действующей в вертикальной плоскости под углом а = 35" к горизонтали, и силой 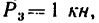действующей вдоль нижнего горизонтального ребра торца бруса.

Определить реакции заделки.

Решение.

1.    Освободим брус от связи (от стены) и заменим ее реакциями (рис. 166, б). Как известно, равновесие балки, жестко заделанной одним концом, обеспечивается двумя реактивными факторами: реактивной силой и реактивным моментом. В данной задаче нагрузки, действующие

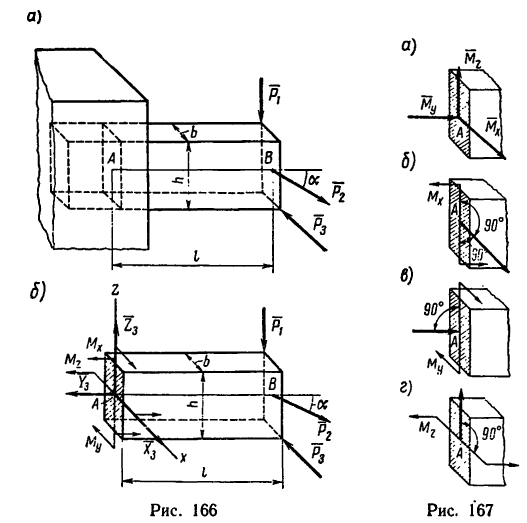
на брус, расположены не в одной плоскости, поэтому нельзя заранее определить, в каких плоскостях расположатся реактивная сила и реактивный момент.

Заменим реактивную силу тремя составляющими: 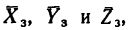, направив их вдоль предварительно выбранных осей координат. Реактивный момент заменим также тремя моментами*— тремя парами сил:

2.    Таким образом, на брус, кроме трех заданных сил, действуют шесть неизвестных реактивных факторов три силы и три момента. Для пространственной системы сил можно составить шесть уравнений равновесия — значит задача статически определима.
* Как известно, пару сил можно тоже представить в виде вектора. Вектор пары сил, так же как и вектор силы, можно разложить на три составляющих вектора, направленных вдоль осей (рис. 167, а), а зачем каждый составляющий вектор пары заменить парой сил, действующей в плоскости, перпендикулярной к тон оси, вдоль которой направлен вектор нары (рис. 167 б, в, г).

3.    Для облегчения составления уравнений равновесия изобразим брус вместе с действующими на него силами в трех проекциях (рис. 168, а) и составим уравнение равновесия.

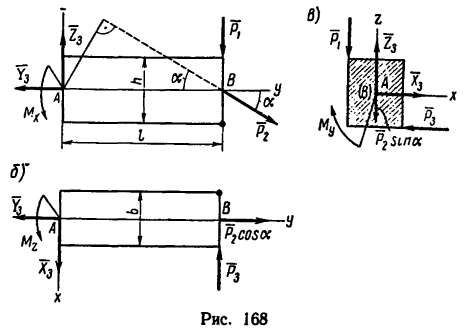
Можно, конечно, при составлении уравнений  пользоваться только одним рис. 166, б:  

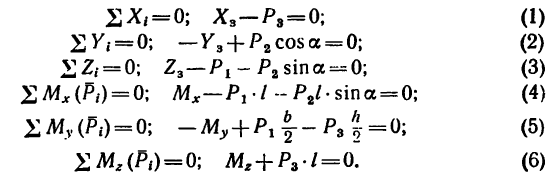
4. Решая эти уравнения, получаем:

• из (1)
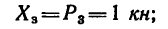
• из (2)
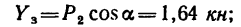
• из (3)
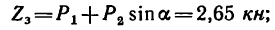
• из (4)
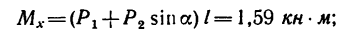
• из (5)
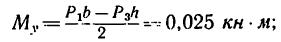
• из (6)

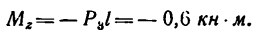
Одной из типичных задач, в которых применяются уравнения равновесия пространственной системы сил, является задача определения реакций опор вала какой-либо машины.

Задачи этого типа можно решать так же, как задачи 115-22 или 116-22, т. е. при помощи проекций вала вместе с векторами заданных и искомых сил на три взаимно перпендикулярные плоскости. Но в некоторых случаях оказывается более рациональным несколько иной прием решения, основанный на приведении сил к оси вала. В качестве примера для такого решения возьмем вал одного из многочисленных видов редукторов *.

Задача №

На вале редуктора жестко укреплены два зубчатых колеса: коническое / и цилиндрическое 2 (рис. 169, а). Левая цапфа вала опирается на подшипник, воспринимающий только радиальную силу давления, действующую перпендикулярно к оси вала, а правая цапфа (пята) опирается на подпятник, т. е. на опору, способную, кроме радиальной силы давления, воспринимать и осевую (силу, действующую вдоль оси вала).

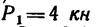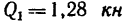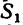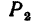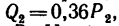На колесо 1 действуют три силы: касательная (окружное усилие); радиальная и осевая = 0,48 кн. Определить в положении равновесия силы и , приложенные к колесу 2, а также реакции опор А и В. Необходимые размеры (в мм) даны на рис. 169, а. Весом вала и колес пренебречь.

Решение.

1.    Заданные и искомые силы, приложенные к колесам 1 и 2, приведем к точкам 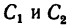на геометрической оси вала (рис. 169, б).

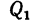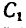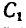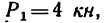Сила = l,28 кн, действующая вдоль радиуса колеса, переносится в точкунепосредственно. Для приведения к точке силы приложим к этой точке уравновешенную систему сил 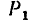и - 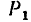и тогда, кроме приведенной силы 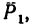образуется пара сил 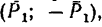отмеченная на рисунке одной черточкой (присоединенная паря сил). При переносе в точку 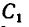силы 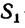= 0,48 кн аналогичным образом появляется пара 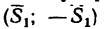отмеченная двумя черточками. Сила 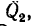, действующая вдоль радиуса колеса 2, переносится в точку 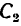непосредственно. 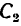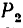При переносе в точку силы образуется пара отмеченная на рисунке тремя черточками.

2.    Освободив вал в точках A и В от опор, заменяем действие опор их реакциями: подшипник А нс препятствует горизонтальному смещению вала, поэтому его реакцию, расположенную в плоскости, перпендикулярной к оси вала, заменяем двумя составляющими: горизонтальной 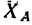и вертикальной 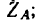подпятник В препятствует смещению вала вдоль его оси, поэтому его реакцию заменяем тремя составляющими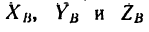(см рис. 169, б).

• Редуктором называется механическое устройство для передачи мощности от двигателя, вал которого вращается с большой скоростью, к рабочей машине, вал которой имеет скорость вращения, в несколько раз меньшую.

3.    При известном навыке решения задач вместо расчетной схемы, показанной на рис. 169, б, можно получить более простую схему (рис. 169, в), на которой вместо пар сил круговыми стрелками обозначены их моменты. Так, круговой стрелкой 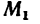обозначен момент пары сил действующей в плоскости,

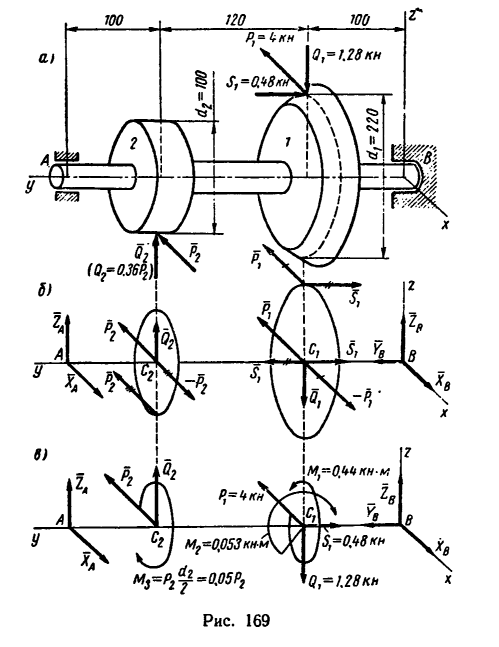
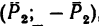перпендикулярной к оси у; —момент пары действующей в плоскости, перпендикулярной к оси х, и - момент пары действующей в плоскости, перпендикулярной к оси у.

Если силы выражать в кн, а плечи пар в м, то получим такие абсолютные числовые значения моментов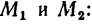

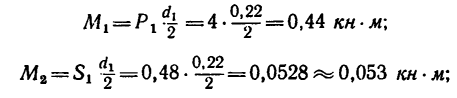
а момент 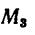выразится так:

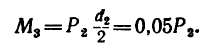
4.    Составим шесть уравнений равновесия.

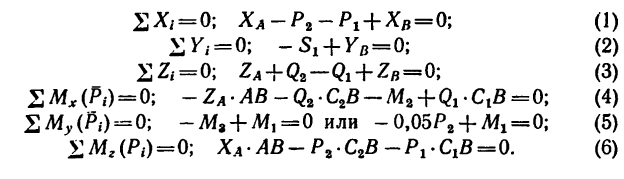
5.    Решая эти уравнения последовательно, получим: из уравнения (5)
Так как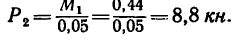

то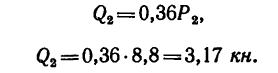
Из уравнения (6)

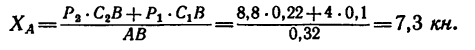
Из уравнения (4)

Реакция 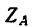 направлена не вверх, как на рис. 169, в, а вниз. Из уравнения (3)

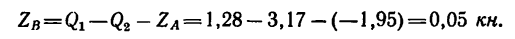
Из уравнения (2)

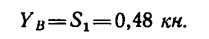
Из уравнения (1)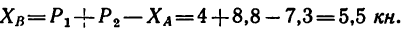

Следующие три задачи рекомендуется решить самостоятельно.