Производная функции одной переменной - определение с примерами решения

Содержание:

Определение производной, её геометрический смысл:

Рассмотрим функцию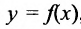

называется разностным отношением (в данной точке). Разностное отношение - это функция, которая определена для всех значений аргумента, кроме 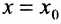. Это дает нам право рассматривать вопрос о существовании предела функции (11.1.1) при .

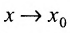Определение 11.1.1. Пусть функция y=f(x) определена в некоторой окрестности точки 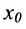и пусть х - некоторая точка этой окрестности, 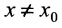. Если отношение

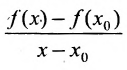имеет предел при 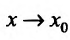, то этот предел называется производной функции f e точке 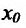и обозначается 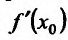, т.е.

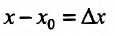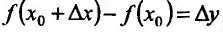Если ввести обозначения и , то формула (11.1.2) запишется в виде:

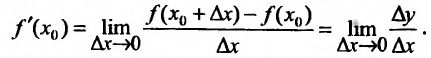
Если для некоторого значения 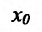выполняется условие

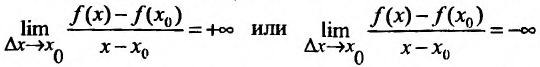, то говорят, что для этого значения 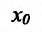существует бесконечная производная, равная л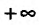ибо,либо.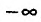

В дальнейшем под выражением «функция имеет производную» мы будем понимать, что функция имеет конечную производную, которую будем обозначать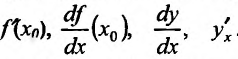

Определение 11.1.2, Если функция f определена в правосторонней (левосторонней) окрестности точки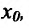 или существует конечный или бесконечный предел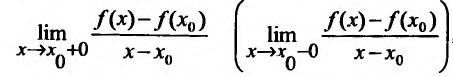

то он называется конечной или бесконечной производной справа (слева) функции f в точке х и обозначается f+(xq) (или f'.(x0)).

Из теоремы 10.2.1 об односторонних пределах следует, что функция f, определенная в некоторой окрестности точки 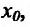, имеет производную 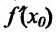тогда и только тогда, когда 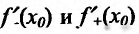суше-ствуют и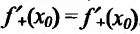. В этом случае

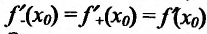
Заметим, что если у функции 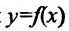существуют правая и левая производные в точке 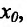, но эти производные не равны друг другу, то у этой функции не существует производной в точке 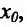Например, функция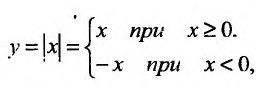

не имеет производной в точке 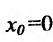, так как,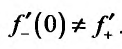. Поскольку правая производная равна: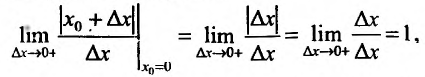

а левая производная равна: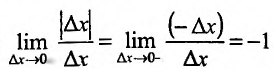

Понятие производной в данной точке связано с понятием касательной к графику функции в этой точке. Чтобы выяснить эту связь, определим, прежде всего, касательную.

Пусть функция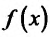 определена на интервале (а; b), непрерывна в точке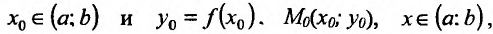 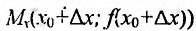. Уравнение секущей, как уравнение прямой, проходящей через две точки 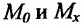имеет вид

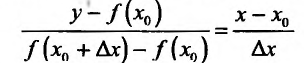
или

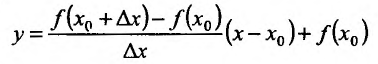
или

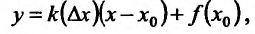
где

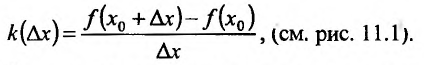
Если существует предельное положение секущей 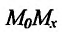при стремлении точки 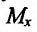графика функции к точке 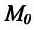(или, что то же самое, при стремлении 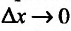), то это предельное положение называется касательной к графику функции 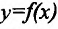в данной фиксированной точке 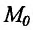этого графика. Отсюда следует, что для того, чтобы существовала касательная к графику функции 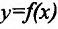в точке 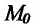достаточно, чтобы существовал предел

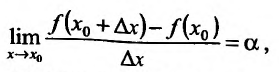
причем указанный предел 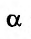равен углу наклона касательной к оси Ох.

Предположим, что функция 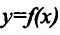имеет в данной точке 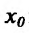изводную. Докажем, что существует касательная к графику фу ции 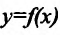в точке 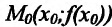, причем угловой коэффициент касательной (т.е. тангенс угла наклона ее к оси Ох) равен производной .

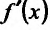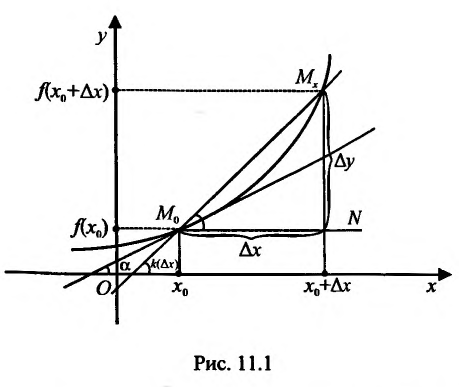
Рассмотрим рис. 11.1. Из треугольника 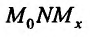найдём

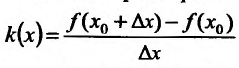и вычислим предел k(х) при.

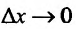Поскольку в точке 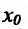существует производная, то существует пред

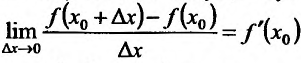но тогда и существ"

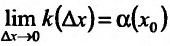. Отсюда и из непрерывности функции f(x) следует, что 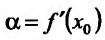. А это означает, что существует касателые графику функции y=f(x) в точке 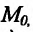, угловой коэффициент ко равен производной функции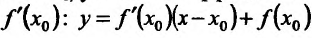

Правила вычисления производных, связанные с арифметическими действиями над функциями

Предположим, что все функции, рассматриваемые ниже, определены в некоторой окрестности точки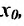

Теорема 11.2.1. Если функция f имеет производную в некоторой точке 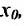, то она непрерывна в этой точке.

Доказательство. Рассмотрим разность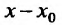 и соответствующее приращение функции 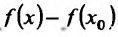. Найдём предел приращения функции при :

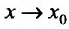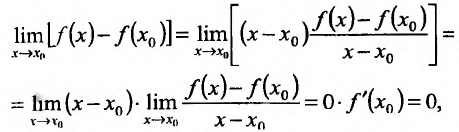
т.е. бесконечно малому приращению независимой переменной соответствует бесконечно малое приращение функции, значит, / непрерывна в точке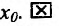

Заметим, что обратная теорема не верна, т.е. функция может быть непрерывной в точке 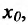но не иметь производной в этой точке. Примером служит функция 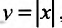которая непрерывна в точке х=0, но, как мы уже показывали в п. 11.1. не имеет в этой точке производной

Теорема 11.2.2. Если функции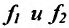 имеют производные в данной точке 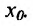то и сумма функций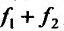, разность функций 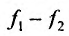имеют производные в точке 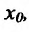которые вычисляются по формулам:

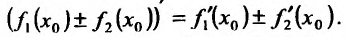
Доказательство. Пусть функции 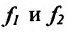имеют производные в точке 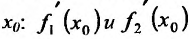. Докажем, что их сумма 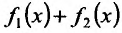так-же имеет в точке 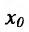производную и 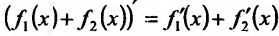Обозначим

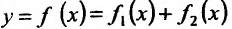и вычислим приращение функции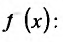

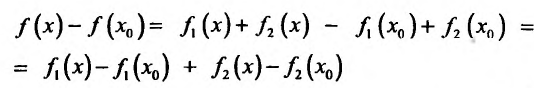
Составим разностное отношение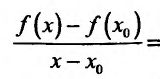

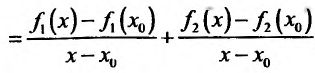
, если 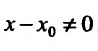, и вычислим предел этого разностного отношения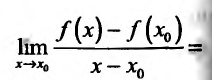 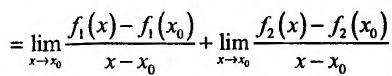Предел суммы равен сумме пределов, так как пределы слагаемых существуют. Пределы слагаемых равны, соответственно, 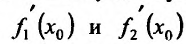. Следовательно, в точке предел правой части равенства существует и он равен 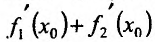• Значит, существует предел левой части, который\ силу определения производной равен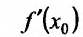. Поскольку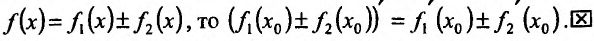

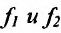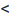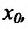Теорема 11.2.3. Пусть функции имеют производные точке , тогда и произведение 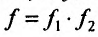имеет в точке 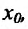производную, причём

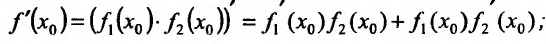
а если 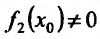, то и частное 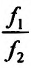также имеет в точке 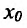проводную, вычисляемую по формуле:

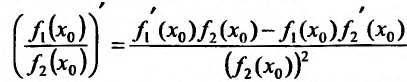
Доказательство. Пусть 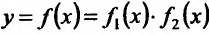. Тогда приращение функции равно 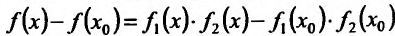. Обозначая 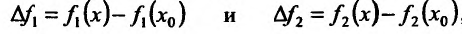, выразим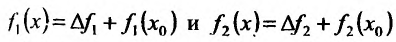

Подставим эти выражения в формулу приращения функции f, получим:

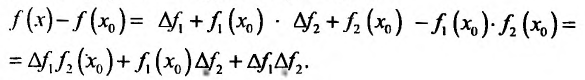
Составим разностное отношение

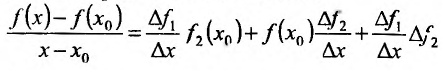
Рассматривая предел разностного отношения при 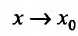, т.е. при 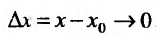, будем иметь

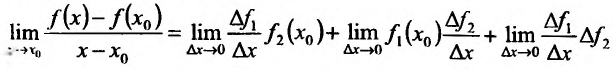
или

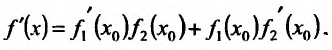
так как 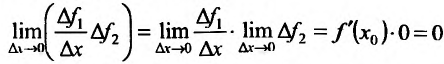(функция 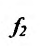имеет производную в точке 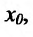следовательно, она непрерывна, и значит).

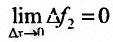Пуста 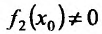. Тогда существует такое h>0, что 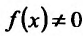для всех 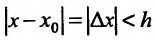. Выбрав 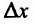такое, что 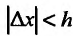, рассмотрим приращение функции

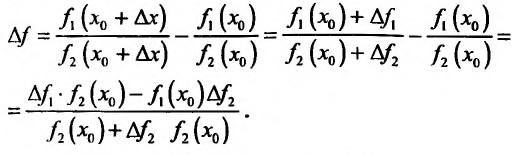
Поэтому 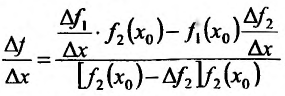Вычислив предел разкостного отношения при 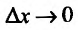и воспользовавшись определением производной, как и при доказательстве предыдущей формулы,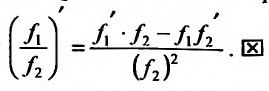

Следствие 11.2.1. Пусть функция f имеет производную в точке 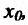, тогда функция cf(x) (с- постоянная) также имеет в этой точке производную, причём '.

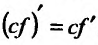Следствие 11.2.2. Пусть функции 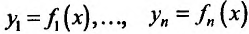имеют производные в точке 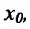, тогда функция 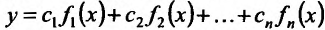также имеет в точке 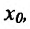производную, причём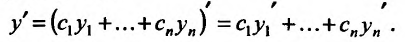

Производные сложной и обратной функций

Определим правила, позволяющие вычислять производные обратных и сложных функций.

Теорема 11.3.1. Пусть функция f определена, непрерывна и строго монотонна в некоторой окрестности точки 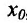и пусть в точке хо существует производная 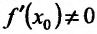, тогда и обратная функция 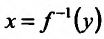, определенная в некоторой окрестности точки 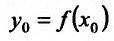имеет производную в точке 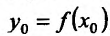, причём 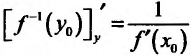т.е. производная обратной функции равна обратной величине производной данной функции.

Доказательство. Зафиксируем некоторую окрестность точки 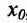, на которой функция f определена, непрерывна и строго монотонна и рассмотрим функцию только в этой окрестности. Тогда существует однозначная обратная функция непрерывная, строго монотонная на некотором интервале, содержащем точку 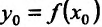(на образе указанной выше окрестности точки 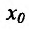и поэтому условия 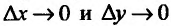эквивалентны).

Зададим аргументу у функции 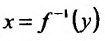произвольное достаточно малое и отличное от нуля приращение 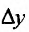. Этому приращению соответствует приращение обратной функции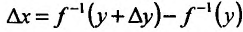, отличное от нуля. Тогда отношение 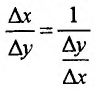имеет предел и 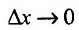при и при 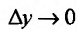, т.е.

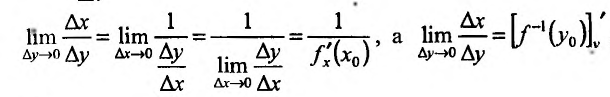, поэтому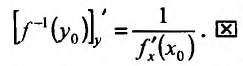

Эта теорема допускает наглядную геометрическую интерпретацию (рис. 11.2).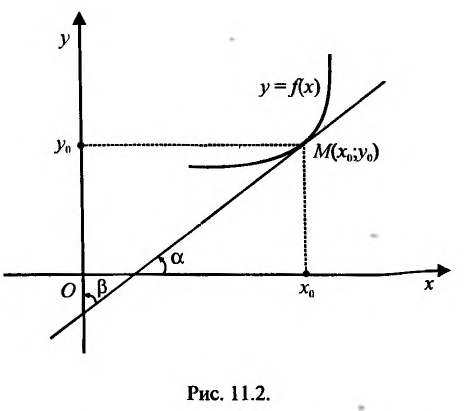

Известно, что производная функции в точке 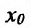равна тангенсу угла наклона касательной к графику функции в точке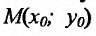

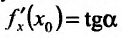
Поскольку у функции 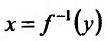аргументом является переменная у, то в силу геометрической интерпретации производной можно утверждать, что производная обратной функции с геометрической точки зрения - это тангенс угла, который образует касательная к графику функции 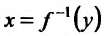в точке М, с положительным направлением оси Оу, т.е. .

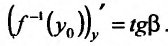Поскольку 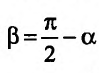, то,

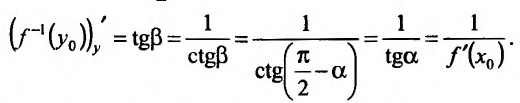
Пример №1

Найти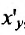, если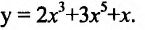

Решение:

Имеем 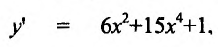тогда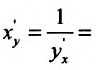

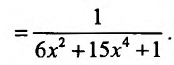
Теорема 11.3.2. Пусть 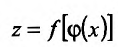- сложная функция, и пусть функция 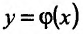имеет производную в точке 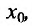, а функция 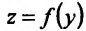имеет производную в точке 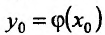. Тогда сложная функция 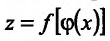так же имеет производную в точке 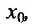причём:

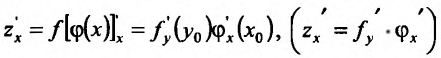
Доказательство. Придадим приращение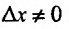 независимой переменной х функции 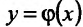. Этому приращению соответствует некоторое приращение 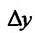функции у, равное 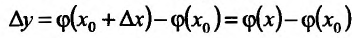. Пусть 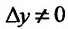. Тогда приращению 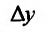соответствует приращение функции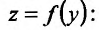 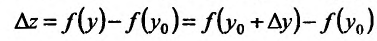и пус^ оно не Равно НУЛЮ

Составим разностное отношение 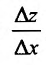, которое представим в виде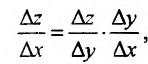

поскольку 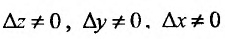. Из непрерывности Дх Ау Ах

функции 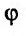следует, что, при 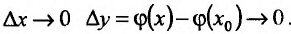. Следовательно,

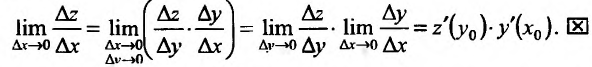
Заметим, что, используя правило вычисления производной сложной функции, можно находить производные функций, заданных неявно

Действительно, пусть функция 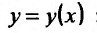задана неявно уравнением F(x,y)= 0. Вычисляя производную правой и левой части тождества 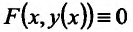как производную сложной функции, находим 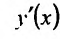разрешая полученное равенство после вычисления производной относительно .

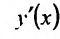Пример №2

Найти 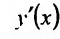, если :

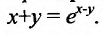
Решение:

Дифференцируем данное уравнение по х, считая у функцией от х:

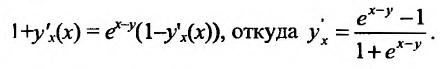
Таблица производных

Для непосредственного вычисления производной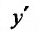 функции 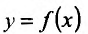на основании определения производной выполняют операции по следующему правилу:

1. выбирают приращение аргумента 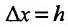, находят соответствующее приращение функции 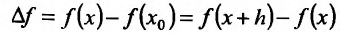и составляют разностное отношение ;
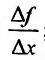2. преобразуют разностное отношение;
3. вычисляют предел преобразованного разностного отношения, при

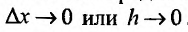
Если предел существует, то и производная существует и она равна пределу разностного отношения.

Применим это правило для определения производных простейших функций.

Свойство 11.4.1. у = с (const).

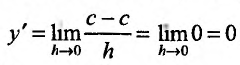,т.е. производная постоянной, равна нулю.

Свойство 11.4.2. у = sin x .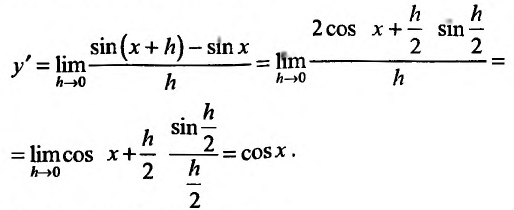

Свойство 11.4.3. у = cos x.

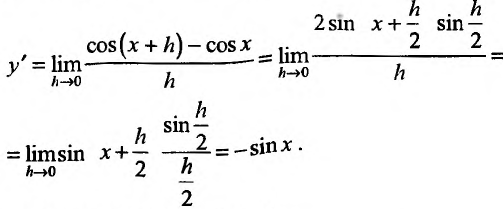
Свойство 11.4.4.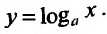

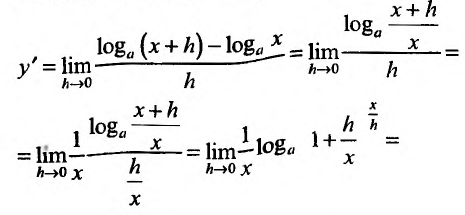
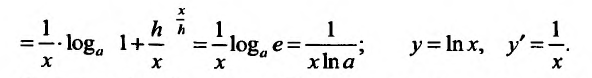
Свойство 11.4.5. у = tg x. Применим правило для производной частного двух функций:

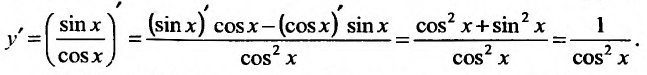
Свойство 11.4.6. у = ctgx Применяя правило дифференцирования частного, будем иметь: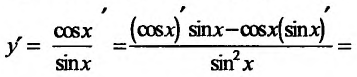

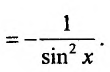
Свойство 11.4.7.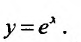

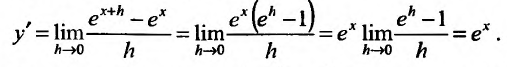
Свойство 14.4.8. 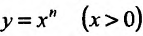. Пользуясь определением логарифма, мы можем представить нашу функцию в виде сложной функции 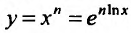. По правилу вычисления производной сложной функции, получим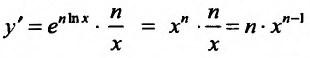

Свойство 11.4.9. у = arcsinх. Если 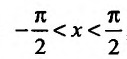то функция 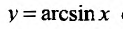обратная по отношению к функции x = siny, и применив правило вычисления производной обратной функции, имеем: 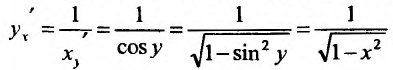, причем у радикала надо брать знак «+», т.к. cos y имеет в интервале 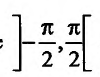знак«+». Аналогично,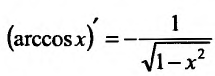

Свойство 11.4.10. у = arctgx. Если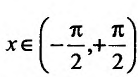 то Функция у = arctg x обратная по отношению к функции x = tg у ; следовательно, 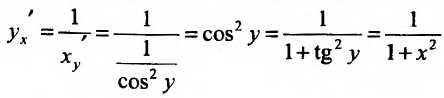. Аналогично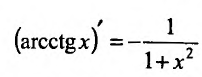

Свойство 11.4.11. 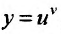, где u и v функции от х ( называется степенно-показательной функцией). Воспользовавшись определением логарифма, заданную функцию 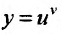можно представить в виде 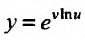. Применяя правило вычисления производной сложной функции, получим:

Свойство 11.4.12. 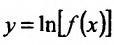, где f(x) - постоянно положительная функция. Применяя правило вычисления производной сложной функции, получим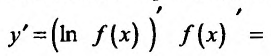 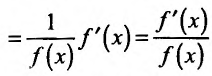. Выражение 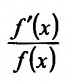называется логарифмической производной.

Приведём таблицу производных простейших элементарных функций:

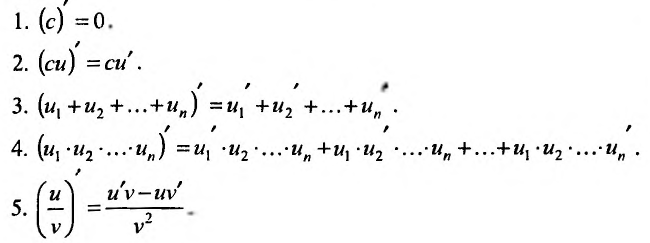
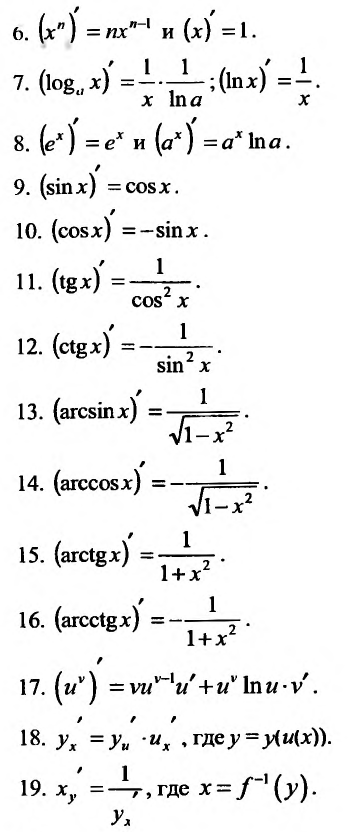
Пример №3

Вычислить производную функции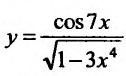

Решение:

Воспользовавшись формулой вычисления производной частного, получим:

• Заказать решение задач по высшей математике

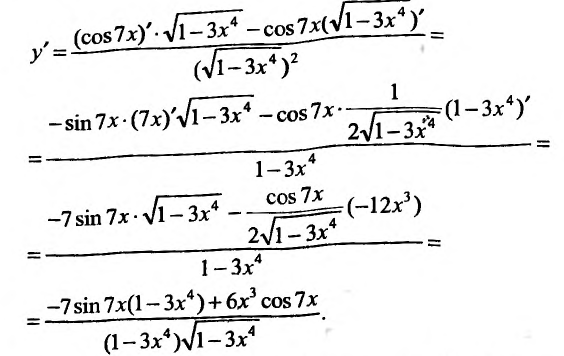
Пример №4

Вычислить производную функции ;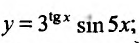

Решение:

Воспользовавшись формулой вычисления производной произведения, получим:

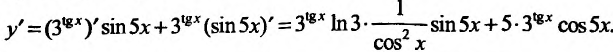
Пример:

Вычислить производную функции у = In arcsin/6х;

Решение:

Воспользовавшись формулой вычисления производной сложной функции, получим:

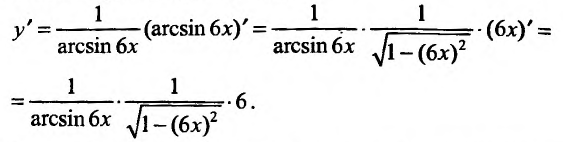
Выведем ещё формулу для вычисления производной параметрически заданных функций, т.е. функций, заданных формулами вида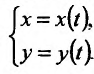

Если функции x = x(t) И y = y(t) имеют в точке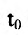 производные и если 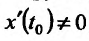, то параметрически заданная функция 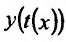также имеет в точке 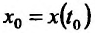производную, причём

В самом деле, по правилу вычисления производной сложной функции имеем 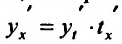. Поскольку t=t(x) - функция, обратная к функции x=x(t), то 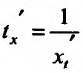. Тогда, подставив значение производной 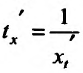в формулу 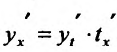.получим (11.4.1).

Производные высших порядков

Производная 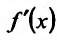функции 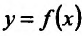, определенной на интервале (а, b) и имеющей производную в каждой точке этого интервала (a,b), представляет собой функцию, также определенную на интервале (a,b). И если эта функция 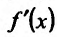имеет производную в некоторой точке, то можно ввести следующее определение:

Определение 11.5.1. Пусть функция f определённая на интервале (а.b), в каждой точке 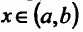имеет производную 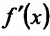и пусть 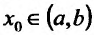. Производная функции 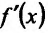в точке 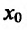называется второй производной функции f и обозначается ,

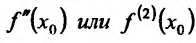т.е.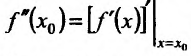

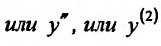
После того, как введено определение второй производной, можно последовательно ввести определение третьей производной, затем четвертой производной, и т.д. Если предположить, что уже введено определение (n-1)-ой производной и что (n-1)-ая производная имеет производную в некоторой точке 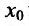интервала (a,b),то эту производную называют n-ой производной (или производной n-ого порядка) функции 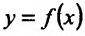в точке 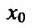и обозначают 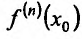или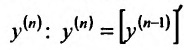

Кроме того считают, что 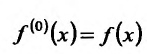. Ясно, что 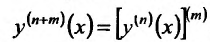- Заметим, что если функция f имеет в точке 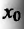. производную порядка n, т.е. если существует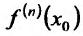. то отскг следует, в силу определения производной, что в некоторой о ности существуют все производные низших порядков.

Определение 11.5.2. Функция f называется n раз непрерывной дифференцируемой на некотором промежутке, если на этом промежутке существует непрерывная производная n-ого порядка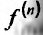 функции f.

По индукции можно доказать, что: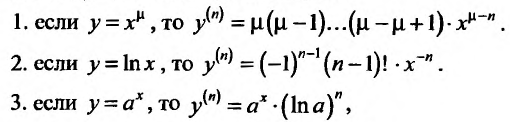

в частности , если

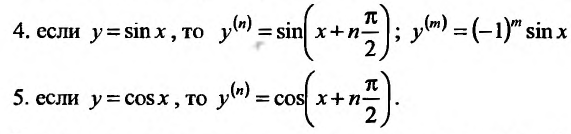
Кроме того, по индукции можно доказать, что сумма функций,, слагаемые которой имеют производные n-го порядка, также имеет производную n-го порядка, вычисляемую по формуле:'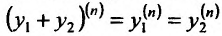 и произведение функций имеет производную n-го порядка, вычисляемую по формуле Лейбница:

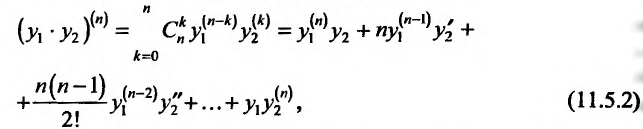
где 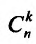- число сочетаний из n элементов по к: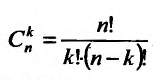

Рассмотрим некоторые производные 2-го порядка:

- для сложной функции 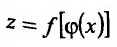вторая производная вычисляется по формуле:

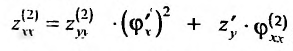
- для обратной функции 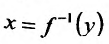вторая производная вычисляется по формуле;

так как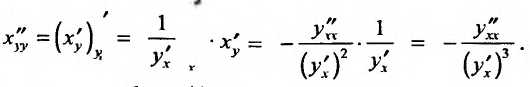

для функции 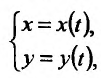заданной параметрически, производная второго порядка вычисляется по формуле:

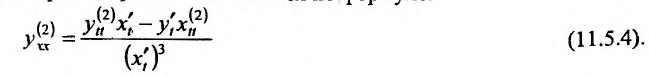
Действительно, так как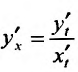, то

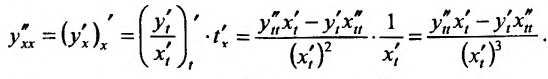
Пример №5

Найти 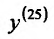если .

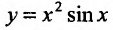Решение:

Полагая в формуле Лейбница (11.5.2) ,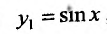

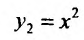и учитывая, что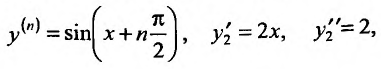

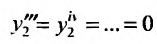, получим:

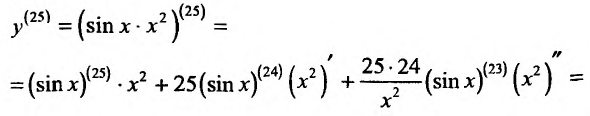
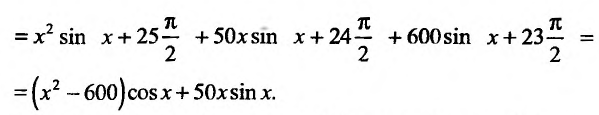
Подчеркнем, что формула Лейбница особенно эффективна в том случае, когда одна из перемножаемых функций имеет лишь конечное число отличных от нуля производных и не представляет затруднения вычисление всех производных другой из перемножаемых функций.