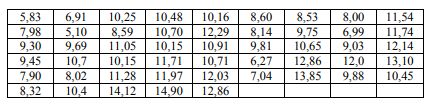
Дана выборка из генеральной совокупности объема. По выборке необходимо выполнить следующие расчеты 5,83 6,91 10,25 10,48 10,16 8,60 8,53 8,00 11,54 7,98 5,10 8,59 10,70 12,29 8,14 9,75 6,99 11,74

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16412
		Прошла проверку преподавателем МГУ
		245 руб.

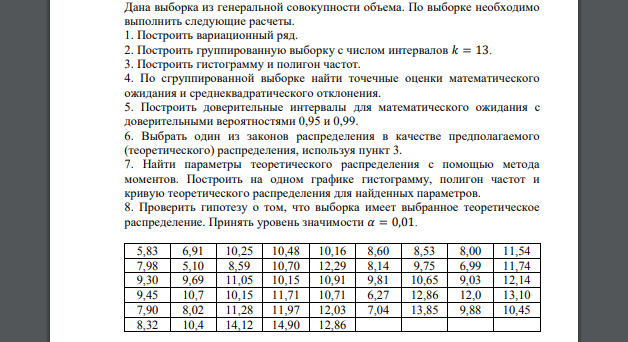
Дана выборка из генеральной совокупности объема. По выборке необходимо выполнить следующие расчеты. 1. Построить вариационный ряд. 2. Построить группированную выборку с числом интервалов 𝑘 = 13. 3. Построить гистограмму и полигон частот. 4. По сгруппированной выборке найти точечные оценки математического ожидания и среднеквадратического отклонения. 5. Построить доверительные интервалы для математического ожидания с доверительными вероятностями 0,95 и 0,99. 6. Выбрать один из законов распределения в качестве предполагаемого (теоретического) распределения, используя пункт 3. 7. Найти параметры теоретического распределения с помощью метода моментов. Построить на одном графике гистограмму, полигон частот и кривую теоретического распределения для найденных параметров. 8. Проверить гипотезу о том, что выборка имеет выбранное теоретическое распределение. Принять уровень значимости 𝛼 = 0,01. 

Решение

Построим вариационный ряд – выборку в порядке возрастания:  2. Найдем размах выборки Число интервалов 𝑁, на которые следует разбить интервал значений признака, задано:  Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Округление шага производится, как правило, в большую сторону. Таким образом, принимаем ℎ = 0,8. За начало первого интервала принимаем такое значение из интервала чтобы середина полученного интервала оказалась удобным для расчетов числом. В данном случае за нижнюю границу интервала возьмём 4,8. Подсчитаем частоту 𝑛𝑖 каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в левый интервал. Относительные частоты (частости) 𝑓𝑖 определим по формуле: Сформируем таблицу значений относительных частот (частостей) для равноотстоящих вариант. Для построения нормированной гистограммы для каждого интервала найдем значение  Интервал Середина интервала Частота 𝑛𝑖 Частость  3. Построим нормированную гистограмму (синим) и полигон (черным) частот. 4. По сгруппированной выборке найдем точечные оценки математического ожидания и среднеквадратического отклонения. Найдем выборочную среднюю 𝑥̅ (точечную оценку математического ожидания). Точечная оценка дисперсии:  −  Точечная оценка среднего квадратического отклонения:  5. Доверительный интервал для математического ожидания a нормально распределенной случайной величины:  такое значение аргумента функции Лапласа, при котором . Для  по таблице функции Лапласа находим 𝑡 из равенства:  Получаем, и доверительный интервал имеет вид:  Для  по таблице функции Лапласа находим 𝑡 из равенства:  Получаем, и доверительный интервал имеет вид: 6. Выбрать один из законов распределения в качестве предполагаемого (теоретического) распределения, используя пункт 3. Вид гистограммы и полигона относительных частот напоминает кривую Гаусса (нормальную кривую), поэтому делаем предварительный выбор закона распределения – нормальный. 7. Найти параметры теоретического распределения с помощью метода моментов. Параметр 𝑎 нормально распределенной генеральной совокупности равен выборочной средней:  Параметр 𝜎 нормально распределенной генеральной совокупности равен: Плотность распределения вероятности нормально распределенной случайной величины имеет вид  математическое ожидание; 𝜎 − среднее квадратическое отклонение. При  получим:  Построим на одном графике нормированную гистограмму (синим), полигон частот (черным) и кривую 𝑓(𝑥) теоретического распределения (красным) для найденных параметров. 8. Проверим гипотезу о том, что выборка имеет выбранное теоретическое распределение при уровне значимости . Вероятность попадания случайной величины в каждый интервал равна приращению функции распределения:  Теоретические частоты определим по формуле  и вычислим значения  Результаты запишем в таблицу Интервал  Получили. Число степеней свободы. По таблице при уровне значимости  находим. Так как , то нет основания отвергать гипотезу о нормальном распределении.