
Теорема обратимости (или взаимности)
Теорема обратимости (или взаимности):
Пассивные линейные электрические цепи обладают важным свойством, известным под названием обратимости. Основанная на этом свойстве теорема обратимости (или взаимности) может быть сформулирована в двух вариантах: применительно к источникам э. д. с. и тока. Ограничимся рассмотрением первого варианта.
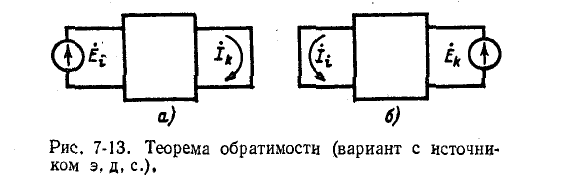
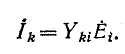
Соответственно э. д. с. 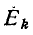 в контуре k (рис. 7-13, б) вызывает ток в контуре i
в контуре k (рис. 7-13, б) вызывает ток в контуре i
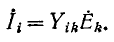
Отсюда следует, что
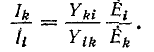
Алгебраические дополнения 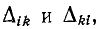 входящие в выражения
входящие в выражения 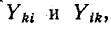 различаются только тем, что в них
различаются только тем, что в них
строки заменены столбцами с учетом того, что их элементы — общие сопротивления контуров заданной цепи — не изменяются от перестановки индексов.
Поэтому 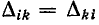 и, следовательно,
и, следовательно,

Электрические цепи, для которых выполняется условие (7-17), называются обратимыми цепями. Для таких цепей имеем:
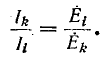
Если принять 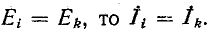
Таким образом, для обратимых цепей справедливо следующее положение: если некоторая э. д. с., находящаяся
в каком-либо контуре электрической цепи, вызывает ток в другом контуре данной цепи, то та же э. д. с., будучи перенесенной во второй контур, вызовет в первом контурный ток с такими же модулем и фазой.
При соответствующем выборе контурных токов ток в ветви равен контурному току. Поэтому данная теорема справедлива также для токов в ветвях.
Использование свойства обратимости пассивных линейных электрических цепей в ряде случаев упрощает расчеты. С этим важным свойством пассивных линейных цепей нам придется неоднократно встречаться далее.
Практическое применение теоремы обратимости иллюстрировано в примерах 7-6 и 7-7.
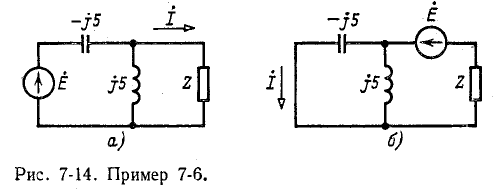
Пример 7-6.
Воспользовавшись теоремой обратимости, вычислить ток 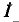 в схеме рис. 7-14, а при любом конечном значении сопротивления Z. Дано: E = 10
в схеме рис. 7-14, а при любом конечном значении сопротивления Z. Дано: E = 10 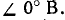
Применение теоремы обратимости облегчает в данном случае расчет тем, что после переноса э. д. с. в ветвь Z (рис. 7-14, б) получается
схема резонанса токов, в которой ток источника равен нулю; поэтому искомый ток, равный току в емкости схемы рис. 7-14,.6, находится как отношение э. д. с. к сопротивлению емкостей ветви:
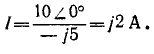
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Теорема об эквивалентном источнике
- Применение матриц к расчету электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
- Метод эквивалентного генератора
- Теоремы теории цепей