Теоремы теории цепей

Содержание:

Основные теоремы теории цепей:

На практике при анализе сложных цепей, когда требуется определить ток или напряжение в отдельной ветви, стремятся свести поставленную задачу к более простой. Это позволяют сделать рассматриваемые далее теоремы теории цепей, которые называют основными: теоремы взаимности и теоремы об эквивалентных генераторах.

Теоремы взаимности (обратимости)

При изучении методов узловых напряжений и контурных токов было отмечено, что определители, составленные из сопротивлений (проводимостей) и независимых источников тока и напряжения линейной цепи, являются симметричными относительно главной диагонали. Свойство симметричности определителей приводит к тому, что если источник воздействия перенести из контура, к которому он подключён, в другой контур, где отсчитывалась реакция, то реакция в первом контуре будет такой же, какой она была во втором контуре. Покажем это для источников напряжения и тока.

Теорема 1:

если независимый источник напряжения, включённый в некоторую ветвь линейной пассивной цепи (рис. 6.1, а, б), вызывает в другой ветви некоторый ток, то этот же источник напряжения, будучи перенесён в эту вторую ветвь, вызовет в первой ветви тот же самый ток.

Доказательство. Пусть в пассивной (например, резистивной) электрической цепи имеется единственный источник напряжения

Тогда при выбранных направлениях отсчётов токов и напряжений согласно (5.25) получаем

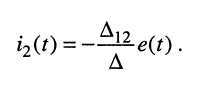       (6.1)

Перенесём источник напряжения во второй контур (рис. 6.1,6) при сохранении нумерации независимых контуров. Тогда из (5.22) при 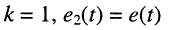и равенстве нулю остальных напряжений 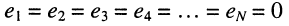получаем

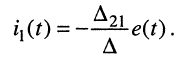         (6.2)

Знаменатели выражений (6.1) и (6.2) содержат один и тот же определитель, который для любой резистивной цепи симметричен относительно главной диагонали, поскольку взаимные сопротивления контуров равны 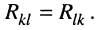Поэтому строки одного из миноров 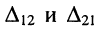являются столбцами другого. Но, как известно, замена в определителе строк его столбцами не меняет значения определителя, т. е. 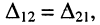и потому

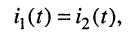       (6.3)

что и требовалось доказать.

В силу отмеченного в лекции 5 принципа дуальности методов узловых напряжений и контурных токов справедлива теорема 2.

Теорема 2:

если независимый источник тока, подключённый к некоторой napq узлов 0-1 линейной пассивной цепи (рис. 6.1, в и г), вызывает между узлами 0-2 второй пары некоторое напряжение, то этот же источник тока, будучи подключён к этой второй паре узлов 0-2, вызывает между узлами 0-1 то же самое напряжение:

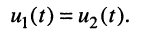
Важно:

теоремы взаимности верны для любых линейных пассивных цепей, но не применимы к цепям, содержащим зависимые источники.
 

Пример 6.1.

Пусть задана схема цепи, изображённая на рис. 6.2, а, в которой ток 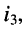 протекающий через элемент 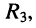известен:

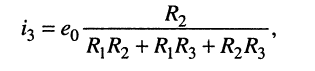
в чём нетрудно убедиться.

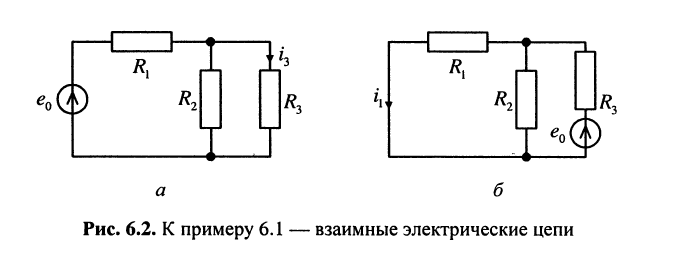
Определим значение тока 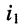(рис. 6.2, б) после переноса источника напряжения 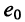в ветвь с сопротивлением 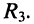На основании теоремы взаимности ответ следует немедленно:

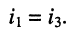
Этот же результат получается и при использовании других известных методов расчёта, с помощью которых читатель может проверить найденное решение.

Пример 6.2.

Найти ток в ветви с сопротивлением 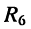при переносе источника напряжения 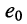в диагональ моста (рис. 6.3, а), т. е. при включении его последовательно с сопротивлением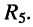

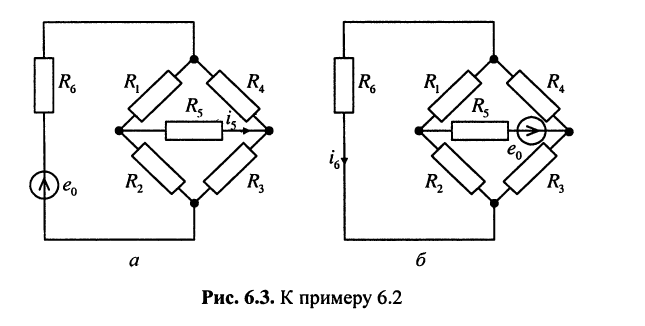
Решение. Как известно, в схеме моста выполняется условие баланса:

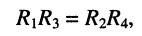
поэтому ток 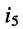равен нулю. Из первой теоремы взаимности следует, что ток 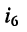в ветви с сопротивлением 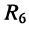(рис. 6.3, б) окажется равным нулю.

Замечание:

Практическое использование теорем взаимности требует проверки возможности их применения.
 

Теоремы об эквивалентных генераторах

Определения:

1. Генератором называется двухполюсная активная электрическая цепь, способная вызывать электрические колебания во внешней по отношению к генератору цепи;
2. Внешняя по отношению к генератору цепь называется нагрузкой генератора.

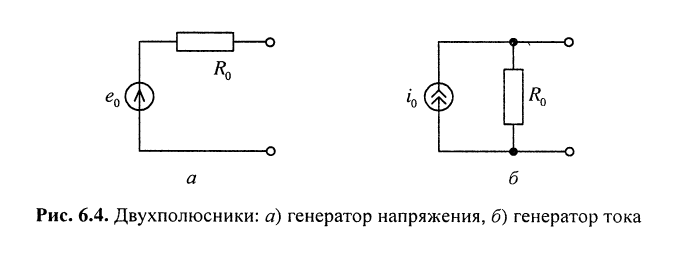
Содержание теорем об эквивалентных генераторах состоит в следующем: любую сколь угодно сложную цепь, состоящую из резистивных элементов, зависимых и независимых источников, относительно некоторой ветви можно заменить активными двухполюсниками. Эти двухполюсники могут представлять собой:

• генератор напряжения в виде последовательно соединённых источника напряжения 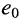  и сопротивления 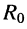(рис. 6.4, а);
• генератор тока в виде параллельно соединённых источника тока 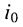и сопротивления 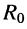(рис/ 6.4, б).

Теорема об эквивалентном генераторе с источником напряжения (теорема Тевенина)

Теорема Тевенинз:

• ток в любой ветви (нагрузке) активной линейной электрической цепи не изменится, если внешнюю относительно этой ветви г/епь заменить цепью из эквивалентного источника напряжения и пассивного двухполюсника, соединённых последовательно; при этом ЭДС источника равна напряжению холостого хода на зажимах ветви; сопротивление пассивного двухполюсника равно сопротивлению цепи относительно этой же ветви при условии, что значения всех ЭДС и задающих токов независимых источников в цепи положены равными нулю.

Доказательство. Рассмотрим активную электрическую цепь, содержащую источники тока и источники напряжения (рис. 6.5, а). Найдём ток 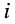 в одной из пассивных её ветвей, имеющей сопротивление  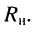Разомкнём эту ветвь, что соответствует режиму холостого хода (рис. 6.5, б). Тогда ток в этой ветви станет равным нулю. Каким-либо образом определим напряжение холостого хода 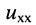на зажимах 12 этой ветви. В цепи (рис. 6.5, а) не произойдёт никаких изменений, если к зажимам 12 подсоединить навстречу друг другу (рис. 6.5, в) два одинаковых источника напряжения 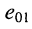и 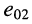с задающим напряжением

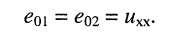
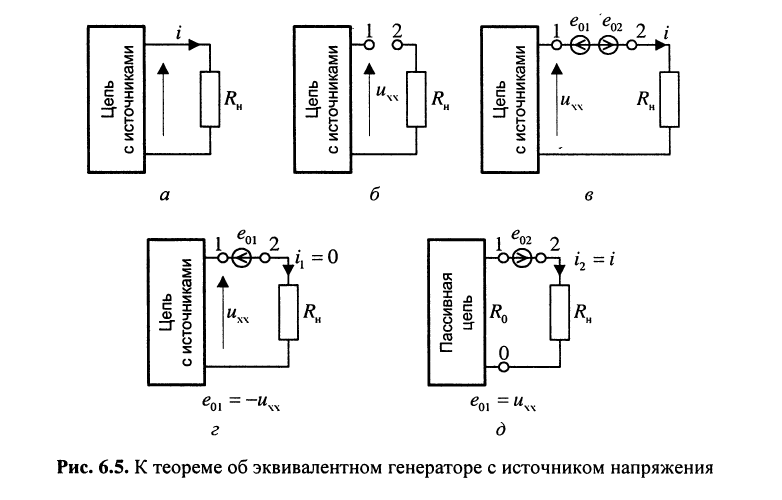
Найдём результирующий ток в нагрузке используя принцип суперпозиции

(наложения). Искомый ток будет складываться из суммы двух составляющих

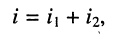
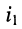 — ток, вызываемый действием всех источников цепи и источника 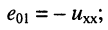этот ток равен нулю 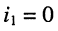(рис. 6.5, г);

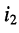— ток, вызываемый действием только одного источника 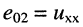при условии, что значения ЭДС и задающих токов всех остальных источников цепи равны нулю (зажимы, к которым подключены источники тока, разомкнуты; зажимы, к которым подключены источники напряжения, замкнуты накоротко), т. е. полученная цепь (рис. 6.5, д) является пассивным двухполюсником с эквивалентным сопротивлением 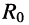относительно зажимов 01.

При этом ток в нагрузке равен

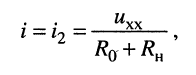     (6.4)

что и требовалось доказать.
 

Теорема об эквивалентном генераторе с источником тока (теорема Нортона)

Теорема Нортона:

• ток в любой ветви (нагрузке) активной линейной электрической цепи не изменится, если внешнюю относительно этой ветви цепь заменить цепью из эквивалентного источника тока и пассивного двухполюсника, соединённых параллельно; при этом задающий ток источника равен току короткого замыкания этой ветви; внутренняя проводимость пассивного двухполюсника равна эквивалентной входной проводимости со стороны разомкнутой ветви.

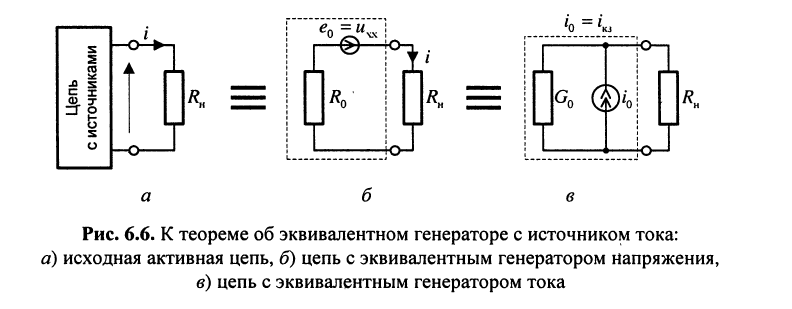
Для доказательства этой теоремы воспользуемся теоремой Тевенина и представим активную цепь (рис. 6.6, а) с помощью эквивалентного генератора напряжения, выделенного на рис. 6.6, б штриховой линией. Если замкнуть отмеченные узлы, найдём ток генератора

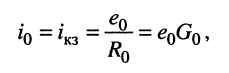         (6.5)

где:

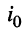•     — задающий ток генератора,
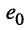•      — ЭДС генератора,
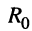•     — внутреннее сопротивление генератора, 
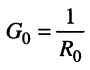•     — внутренняя проводимость генератора.

Выражение (6.5) показывает, что внутреннее сопротивление генератора равно

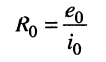             (6.6)

отношению напряжения на разомкнутых зажимах генератора к току, который проходит через его замкнутые накоротко зажимы.

Условия эквивалентности двух схем замещения генераторов

Схемы замещения генератора с источником напряжения (рис. 6.7, а)  и  с  источником тока (рис. 6.7, б), конечно же, должны быть эквивалентны. Смысл эквивалентности этих схем замещения состоит в том, что каждая из них равноправна и может использоваться в качестве схемы замещения генератора с чисто активным внутренним сопротивлением. Тем не менее, необходимо знать, при каких условиях достигается желаемая эквивалентность.

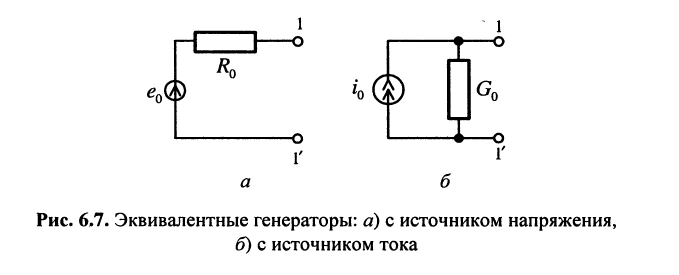
Рассматриваемые генераторы отличаются от идеальных источников наличием в их схемах замещения пассивных двухполюсников R0 и Go, которые характеризуют внутреннее сопротивление (или внутреннюю проводимость) генератора. Наличие внутреннего сопротивления (внутренней проводимости) обусловливает зависимость напряжения, развиваемого генератором на зажимах нагрузки, и тока в нагрузке от свойств самой нагрузки. Этим генератор отличается от источника. Источник — это идеализированный генератор, внутренне сопротивление которого или равно нулю (источник напряжения) или бесконечно велико (источник тока). Свойства идеального генератора не зависят от нагрузки (см. лекцию 3).

Применяя теорему Тевенина к цепи, схема которой изображена на рис. 6.7, б, получаем условие, при котором схема замещения генератора с источником тока эквивалентна схеме замещения генератора с источником напряжения':

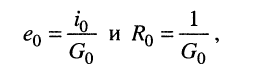                                                                                            (6.7)

при выполнении которого напряжение на разомкнутых зажимах генератора со схемой замещения  рис. 6.7, б оказывается равным 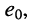 а ток при коротком замыкании зажимов генератора со схемой замещения рис. 6.7, а оказывается равным  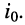Соотношение (6.7) показывает также, что внутреннее сопротивление генератора

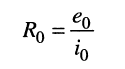
равно отношению напряжения на разомкнутых зажимах генератора к току, который проходил бы через его замкнутые накоротко зажимы.

Пример 6.3.

Найти ток в ветви с сопротивлением 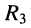в цепи, схема которой изображена на рис. 6.8, а. Задачу решить с применением теорем Тевенина и Нортона.

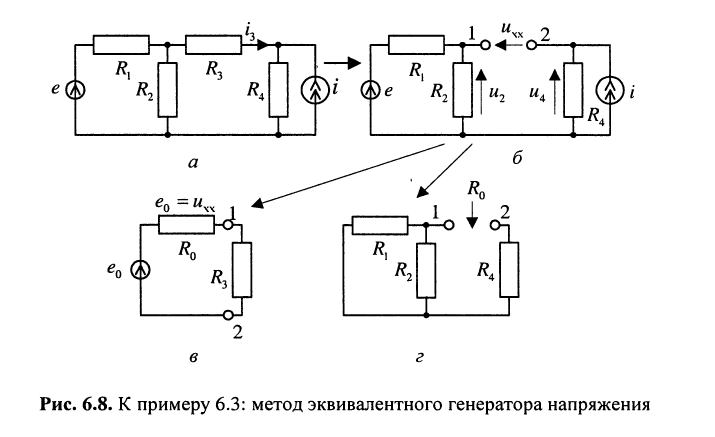
Решение на основании теоремы Тевенина:

• найдём напряжение холостого хода 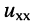 на зажимах 1-2, для чего рассмотрим схему рис. 6.8, б; это напряжение равно разности между напряжениям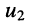и и 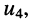 развиваемыми на резисторах 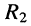и 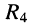соответственно

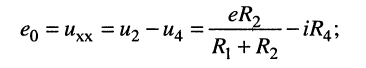
•    получаем схему с эквивалентным генератором (рис. 6.8, в), ЭДС которого равна 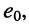а внутреннее сопротивление 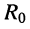требуется определить;

•    внутреннее сопротивление эквивалентного генератора 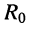найдём, согласно теореме Тевенина, при отключённых источниках напряжения и тока, т. е. пр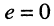и и 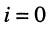в схеме рис. 6.8, б тогда получаем рис. 6.8, г, где параллельно соединённые резисторы 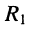и 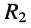соединены последовательно с резистором 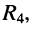поэтому имеем

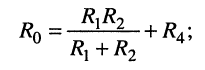
•    теперь легко определить искомый ток из рис. 6.8, в

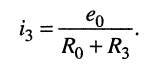
Решение на основании теоремы Нортона: 

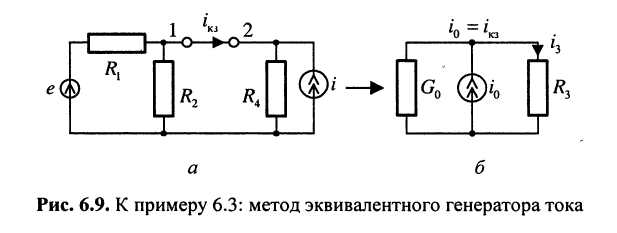
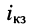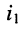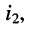найдём ток короткого замыкания  на зажимах 1-2, для чего из рис. 6.8, а получим схему, изображённую на рис. 6.9, а; для этого воспользуемся методом наложения; это означает, что ток представит собой разность между токами и получаемыми от источника напряжения при отключённом источнике тока и от источника тока при отключённом источнике напряжения соответственно:

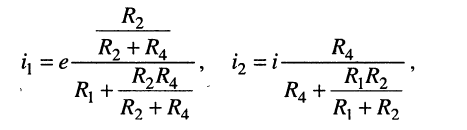
•    теперь можно изобразить схему с эквивалентным генератором тока, внутреннее сопротивление которого 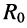определено ранее;

•    искомый ток определяется из рис. 6.9, б:

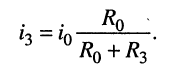
Пример 6.4.

В схеме рис. 6.10, а заменить генераторы с источниками напряжения эквивалентными генераторами с источниками тока.

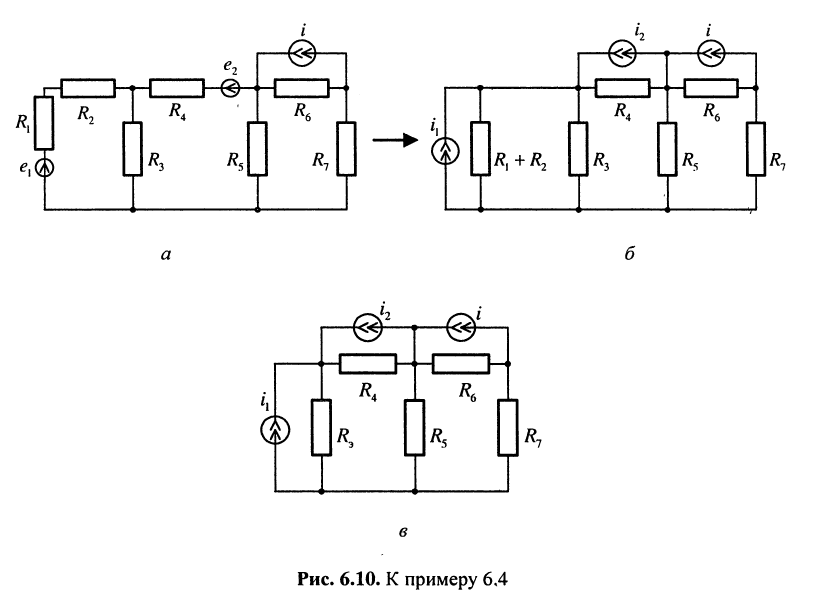
Решение.  Внутренним сопротивлением генератора с источником напряжения 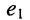можно считать сумму последовательно соединённых сопротивлений 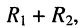тогда в соответствии с условием эквивалентности источников напряжения и тока имеем

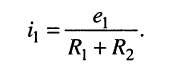
Аналогично из источника 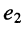получаем

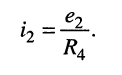
Эти результаты отражены на рис. 6.10, б, где сопротивления  соединены параллельно, поэтому можно вычислить эквивалентное сопротивление

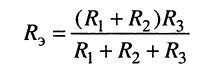
и установить его в схему (рис. 6.10, в).