Трапеция и ее свойства с определением и примерами решения

Содержание:

Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

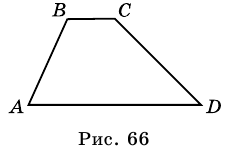
На рисунке 66 изображена трапеция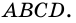

Свойства трапеции

Рассмотрим некоторые свойства трапеции.

1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.

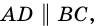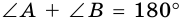Так как  то  (как сумма внутренних односторонних углов). Аналогично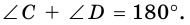

2. Трапеция является выпуклым четырехугольником.

Поскольку 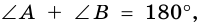то 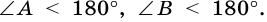Аналогично 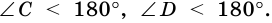Следовательно, трапеция - выпуклый четырехугольник. 

Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.

Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 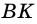- высота трапеции

Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 - прямоугольная трапеция 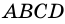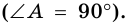Очевидно, что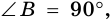 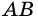  является меньшей боковой стороной прямоугольной трапеции и ее высотой.

Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 - равнобокая трапеция

Свойства равнобокой трапеции

Рассмотрим некоторые важные свойства равнобокой трапеции.

1. В равнобокой трапеции углы при основании равны.

Доказательство:

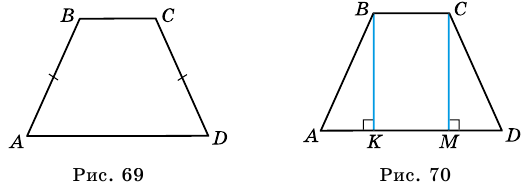
1) Пусть в трапеции 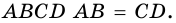Проведем высоты трапеци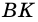и и 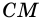из вершин ее тупых углов 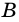и 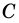(рис. 70). Получили прямоугольник 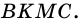Поэтому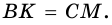

2) 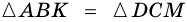 (по катету и гипотенузе). Поэтому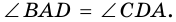

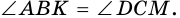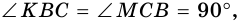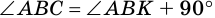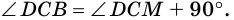3) Также Но поэтому и Следовательно,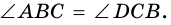

2. Диагонали равнобокой трапеции равны.

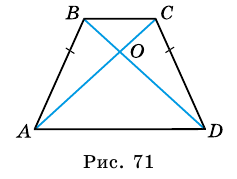
Доказательство:

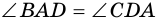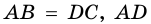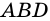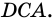Рассмотрим рисунок 71. (как углы при основании равнобокой трапеции), - общая сторона треугольников и Поэтому 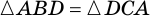(по двум сторонам и углу между ними). Следовательно,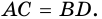

Пример:

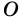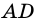 - точка пересечения диагоналей равнобокой трапеции с основаниями и 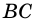 (рис. 71). Докажите, что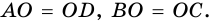

Доказательство:

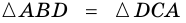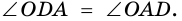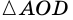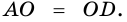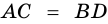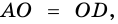(доказано выше). Поэтому По признаку равнобедренного треугольника - равнобедренный. Поэтому Поскольку  и то 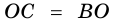 (так как ). 

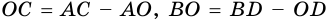Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.

Доказательство:

1) Пусть в 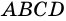 углы при большем основании 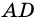равны (рис. 70), то есть 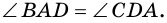Проведем высоты 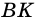и 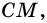они равны.

2) Тогда 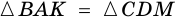(по катету и противолежащему углу). Следовательно, 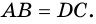Таким образом, трапеция равнобокая, что и требовалось доказать. 

А еще раньше...

Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» - однокоренные).

В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.

Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие - не параллельны.

Свойство средней линии трапеции

Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.

Рассмотрим свойство средней линии трапеции.

Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство:

Пусть 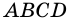- данная трапеция, 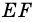- ее средняя линия (рис. 109). Докажем, что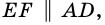 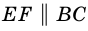  и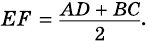

1) Проведем луч 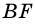до его пересечения с лучом 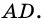Пусть 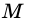- точка их пересечения. Тогда 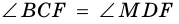(как внутренние накрест лежащие при параллельных прямых  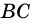и 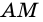и секущей 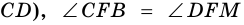(как вертикальные), 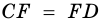(по условию). Следовательно, 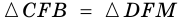(по стороне и двум прилежащим углам), откуда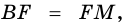 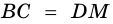  (как соответственные стороны равных треугольников).

2) Поскольку 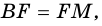 то 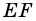- средняя линия треугольника  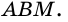Тогда, по свойству средней линии треугольника,  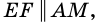а значит,  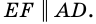Но так как  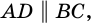то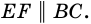

3) Кроме того,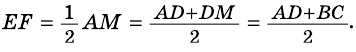

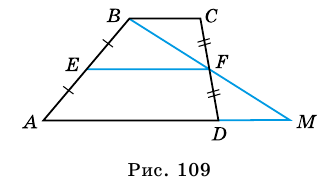
Пример:

Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.

Доказательство:

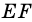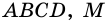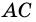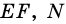Пусть - средняя линия трапеции - точка пересечения и - точка пересечения 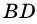и 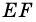(рис. 110). Пусть  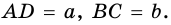Докажем, что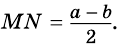 

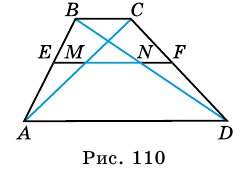
1) Так как 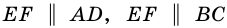и 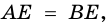 то, по теореме Фалеса, 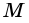-середина 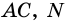- середина  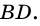Поэтому 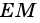- средняя линия треугольника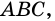 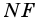 — средняя линия треугольника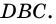

Тогда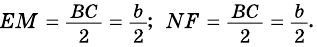

2) 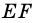- средняя линия трапеции, поэтому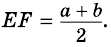

3)

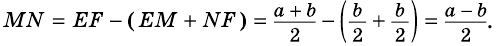
Пример:

В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции - 48 см.

Решение:

Пусть - данная трапеция, - ее средняя линия, 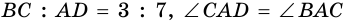(рис. 111).

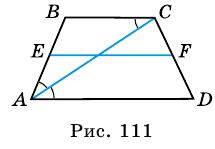
1) Обозначим 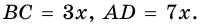Тогда

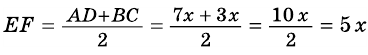
2) 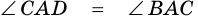(по условию). 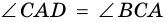(как внутренние накрест лежащие при параллельных прямых  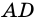и 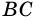и секущей  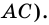Поэтому  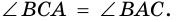Следовательно, 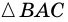- равнобедренный, у которого 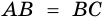(по признаку равнобедренного треугольника). Но 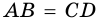(по условию), значит,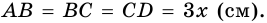

3) Учитывая, что 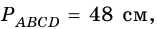 получим уравнение: 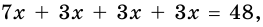откуда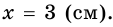

4)    Тогда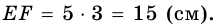

Ответ. 15 см.

А еще раньше...

То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).

О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).