
Дифференциальные уравнения первого порядка с примерами решения
Содержание:
Экономические задачи, приводящие к дифференциальным уравнениям:
Понятие дифференциального уравнения является одним из основных математических понятий. Дифференциальные уравнения возникают в том случае, когда различные состояния изучаемого явления или процесса, в том числе и экономического, удается описать аналитически зависимостью между некоторыми параметрами и их производными или дифференциалами.
Рассмотрим на экономических примерах составление дифференциальных уравнений.
Пример:
Пусть полные издержки К являются функцией объема производства х, т. е. К = К(х), и пусть известно, что предельные издержки для всех значений х равняются средним издержкам. Требуется определить функцию полных издержек (затрат производства).
Решение:
Предположим, что объем производства продукции увеличился^ на 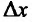
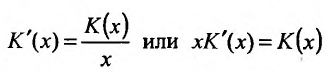 т. е. мы получили уравнение, которос содержит производную неизвестной функции К и саму функцию. Такое уравнение называется дифференциальным уравнением первого порядка. Таким образом, мы рассмотрели задачу о нахождении функции издержек производства по известным предельным издержкам, которая сводится к решению дифференциального уравнения.
т. е. мы получили уравнение, которос содержит производную неизвестной функции К и саму функцию. Такое уравнение называется дифференциальным уравнением первого порядка. Таким образом, мы рассмотрели задачу о нахождении функции издержек производства по известным предельным издержкам, которая сводится к решению дифференциального уравнения.
Пример:
Пусть эластичность 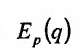 спроса q относительно цены р на некоторый товар описывается функцией
спроса q относительно цены р на некоторый товар описывается функцией 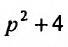 , т. с. известен закон изменения спроса на данный товар, если цена изменяется на 1%. Определим по данному закону функциональную зависимость между спросом на данный товар и его ценой.
, т. с. известен закон изменения спроса на данный товар, если цена изменяется на 1%. Определим по данному закону функциональную зависимость между спросом на данный товар и его ценой.
Решение:
Поскольку изменению цены на 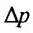 , соответствует изменение спроса на
, соответствует изменение спроса на 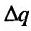 , то величины
, то величины 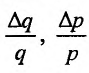 характеризуют относитсльное изменение спроса и цены.
характеризуют относитсльное изменение спроса и цены.
Предел отношения относительного приращения спроса к относительному приращению цены называется эластичностью спроса относительно цены: 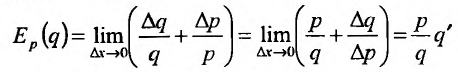
Поэтому если эластичность является известной функцией
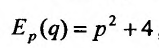 , то получим уравнение
, то получим уравнение 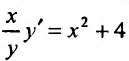 , содержащее неизвестную функцию и ее производную, т. е. дифференциальное уравнение.
, содержащее неизвестную функцию и ее производную, т. е. дифференциальное уравнение.
Таким образом, мы рассмотрели экономические задачи, приводящие к уравнениям, содержащим вместе с неизвестной функцией ее производную.
Сформулируем теперь определение таких уравнений и рассмотрим методы их решения.
Понятие о дифференциальном уравнении и его решении
Определение 22.2.1. Обыкновенным дифференциальным уравнением n-го порядка называется соотношение вида:

где F - известная функция своих аргументов, заданная в некоторой области; х - неизвестная переменная; у - функция переменной х, подлежащая определению; 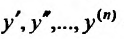 - ее производные.
- ее производные.
Заметим, что некоторые из величин 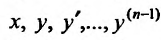 или даже все могут и не входить в соотношение (22.2.1), но обязательно входит n-ая производная
или даже все могут и не входить в соотношение (22.2.1), но обязательно входит n-ая производная 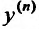 , так как иначе соотношение (22.2.1) уже не будет дифференциальным уравнением n-го порядка.
, так как иначе соотношение (22.2.1) уже не будет дифференциальным уравнением n-го порядка.
Порядком дифференциального уравнения называется наивысший порядок производной искомой функции, фигурирующей в уравнении.
Решением дифференциального уравнения (22.2.1) называется такая функция 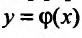 , которая, будучи подставлена в это уравнение, обращает его в тождество:
, которая, будучи подставлена в это уравнение, обращает его в тождество: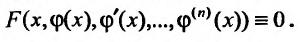
Вначале мы рассмотрим уравнение 
называемое дифференциальным уравнением первого порядка, частным случаем которого является уравнение, разрешенное относительно производной 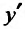 :
:

где функция f(x, у) задана в некоторой области D плоскости хОу. Тогда будем говорить, что и дифференциальное уравнение (22.2.3) задано в области D. Кривая, соответствующая решению 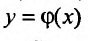 уравнения (22.2.2) или (22.2.3) называется интегральной кривой.
уравнения (22.2.2) или (22.2.3) называется интегральной кривой.
Например, дифференциальным уравнением первого порядка будет уравнение 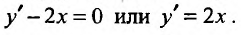
Изменение производительной силы труда может быть описано дифференциальным уравнением первого порядка: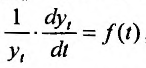
где 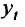 - показатель, характеризующий производительность труда в период времени t;
- показатель, характеризующий производительность труда в период времени t; 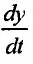 абсолютный прирост производительности труда в единицу времени (например, за год) или скорость абсолютного роста в единицу времени; •
абсолютный прирост производительности труда в единицу времени (например, за год) или скорость абсолютного роста в единицу времени; •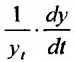 относительная скорость роста производительности труда в единицу времени;
относительная скорость роста производительности труда в единицу времени;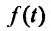 - функция зависящая от времени, характеризующая относительную скорость роста.
- функция зависящая от времени, характеризующая относительную скорость роста.
Простейшая модель воспроизводства национального дохода описывается уравнением:
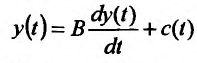
где В - капиталоемкость национального дохода (отношение производственного накопления к приросту национального дохода), В - называют акселератором; c(t) - динамика национального дохода, определяется траекторией c(t): национальный доход направляется на расширение производства и на потребление.
Задача теории дифференциальных уравнений состоит в нахождении решения дифференциального уравнения, а процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения. Часто решение 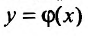 находят в неявном виде:
находят в неявном виде:

Равенство (22.2.4) и определяет функцию 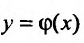 , являющуюся решением уравнения (22.2.3).
, являющуюся решением уравнения (22.2.3).
Заметим еще, что иногда интегральную кривую получают в параметрическом виде:

где вспомогательный параметр t изменяется в некотором промежутке 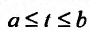 и выполняется тождество:
и выполняется тождество:
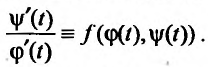
Пример:
Пусть дано дифференциальное уравнение
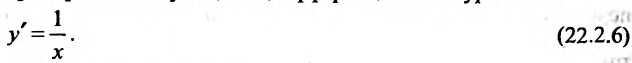
Покажем, что равенство

определяет решение 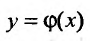 уравнения (22.2.6).
уравнения (22.2.6).
Решение:
Действительно, дифференцируя (22.2.7) получим
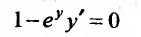
и подставляя в это равенство 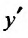 из (22.2.6), получим тождество 1 х-еу
из (22.2.6), получим тождество 1 х-еу
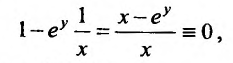
в силу (26.2.7).
Итак, мы показали, что существует решение 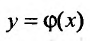 дифференциального уравнения первого порядка заданное в неявном виде.
дифференциального уравнения первого порядка заданное в неявном виде.
Общее решение дифференциального уравнения первого порядка
Частный случай уравнения
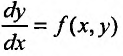 (22.3.1)
(22.3.1)
изучается в интегральном исчислении, именно там рассматривается уравнение
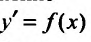 (22.3.2)
(22.3.2)
По заданной производной ищется функция, производная которой равна 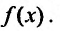 Известно из интегрального исчисления, что решения этого уравнения задаются формулой
Известно из интегрального исчисления, что решения этого уравнения задаются формулой
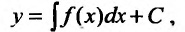 (22.3.3) где С - произвольная постоянная. Отсюда видим, что уравнение (22.3.2) имеет бесконечное множество решений, отличающихся на постоянную величину С. Далее мы увидим, что и для уравненияпервого порядка
(22.3.3) где С - произвольная постоянная. Отсюда видим, что уравнение (22.3.2) имеет бесконечное множество решений, отличающихся на постоянную величину С. Далее мы увидим, что и для уравненияпервого порядка 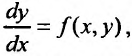 при довольно общих предположениях относительно
при довольно общих предположениях относительно 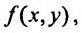 существует бесконечное множество решений, именно семейство решений
существует бесконечное множество решений, именно семейство решений 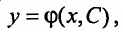 содержащее произвольную постоянную С . Решение вида (22.3.4) с произвольной постоянной С называют общим решением уравнения (22.3.1), которое может быть найдено и в неявном виде:
содержащее произвольную постоянную С . Решение вида (22.3.4) с произвольной постоянной С называют общим решением уравнения (22.3.1), которое может быть найдено и в неявном виде:
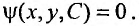 Всякое же решение, полученное из общего при конкретном значении постоянной С, называется частным решением.
Всякое же решение, полученное из общего при конкретном значении постоянной С, называется частным решением.
Пример №1
Пусть дано дифференциальное уравнение: 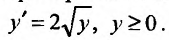 (22.3.5)
(22.3.5)
Общим решением этого дифференциального уравнения будет функция:
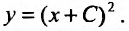 (22.3.6)
(22.3.6)
Пологая С = 1, получим частное решение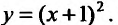 Но
Но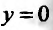 является также решением (22.3.5), хотя его нельзя получить из (22.3.6) ни при каком значении С.
является также решением (22.3.5), хотя его нельзя получить из (22.3.6) ни при каком значении С.
Решение, которое нельзя получить из общего при конкретном значении С, называется особым решением.
Часто, особенно в приложениях, требуется найти решение задачи Коши (начальной задачи), т.е. требуется найти решение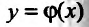 уравнения (22.3.1) обладающее свойством
уравнения (22.3.1) обладающее свойством
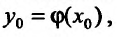 (22.3.7)
(22.3.7)
где 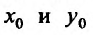 наперед заданные числа, которые называются начальными значениями. Таким образом, в задаче Коши требуется найти решение
наперед заданные числа, которые называются начальными значениями. Таким образом, в задаче Коши требуется найти решение 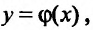 которое проходило бы через наперед заданную точку
которое проходило бы через наперед заданную точку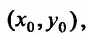 в которой функция
в которой функция 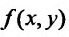 определена. Теперь можно уточнить определение общего решения дифференциального уравнения первого порядка, т.е. справедливо опрсделе-26.3.1.
определена. Теперь можно уточнить определение общего решения дифференциального уравнения первого порядка, т.е. справедливо опрсделе-26.3.1.
Определение 22.3.1. Общим решением дифференциально уравнения первого порядка, определенного в области D, называется функция 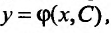 удовлетворяющая условиям:
удовлетворяющая условиям:
а) при любом конкретном значении постоянной величины С она определяет частное решение;
б) для любых начальных условий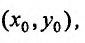 принадлежащих области определения дифференциального уравнения, существует знчение С* такое, что выполняется равенство:
принадлежащих области определения дифференциального уравнения, существует знчение С* такое, что выполняется равенство: 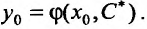
Рассмотрим теперь геометрическую интерпретацию дифферциального уравнения первого порядка. Пусть на плоскости зада прямоугольная система координат 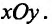 Тогда решению
Тогда решению 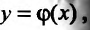 или
или 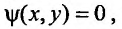 или
или 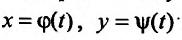 уравнения (22.3.1), как уже говорили, будет соответствовать интегральная кривая. Предложим, что правая часть уравнения (22.3.1) определена и конечна каждой точке некоторой области D плоскости
уравнения (22.3.1), как уже говорили, будет соответствовать интегральная кривая. Предложим, что правая часть уравнения (22.3.1) определена и конечна каждой точке некоторой области D плоскости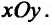 Проведем через каждую точку
Проведем через каждую точку 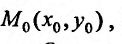 (рис 22.1), этой области, отрезок Т, составляющий с осью
(рис 22.1), этой области, отрезок Т, составляющий с осью 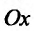 угол
угол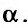 Тангенс этого угла равен значению правой части уравнения (22.3.1) в точке
Тангенс этого угла равен значению правой части уравнения (22.3.1) в точке 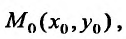 т. е.
т. е. 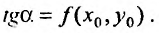 Отметим, что оба направления указанного отрезка для нас безразличны. Таким образом, можно считать, что уравнение (22.3.1) определяет некоторое поле направлений или поле линейных элементов. Ясно, что дифференциальное уравнение (22.3.1) выражает геометрически тот факт, что направление касательной в каждой точке интегральной кривой совпадает с направлением поля в этой точке.
Отметим, что оба направления указанного отрезка для нас безразличны. Таким образом, можно считать, что уравнение (22.3.1) определяет некоторое поле направлений или поле линейных элементов. Ясно, что дифференциальное уравнение (22.3.1) выражает геометрически тот факт, что направление касательной в каждой точке интегральной кривой совпадает с направлением поля в этой точке.
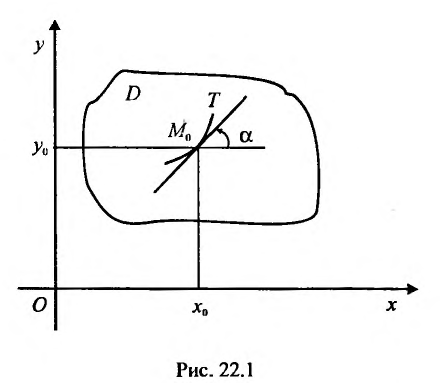
Из выше сказанного вытекает, что всякое дифференциальное уравнение первого порядка выражает некоторое общее свойство касательных всех его интегральных кривых. И задача состоит в том, чтобы по этому свойству касательных к интегральным кривым восстановить само семейство интегральных кривых.
Пример №2
Пусть дано уравнение 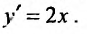
Его решением является семейство функций 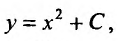 где
где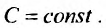 Интегральные кривые семейства парабол обладают общим свойством: в каждой точке
Интегральные кривые семейства парабол обладают общим свойством: в каждой точке 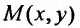 области определения уравнения угловой коэффициент касательной
области определения уравнения угловой коэффициент касательной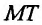 к интегральной кривой равен удвоенной абсциссе этой точки:
к интегральной кривой равен удвоенной абсциссе этой точки: 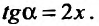
Теоремы существования и единственности
Выше мы говорили о решении уравнения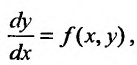 предполагая, что оно существует.
предполагая, что оно существует.
Сформулируем теперь теоремы (без доказательства), которые гарантируют существование и единственность решения.
Теорема Пеано (теорема существования). Для того, чтобы уранение 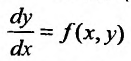 имело хотя бы одно решение достаточно, чтобы его правая часть была непрерывна.
имело хотя бы одно решение достаточно, чтобы его правая часть была непрерывна.
Теорема Пикаро (теорема единственности). Пусть дано уравнение 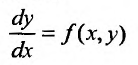 (22.4.1) и поставлено начальное условие
(22.4.1) и поставлено начальное условие 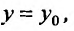 при
при 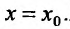 Предположим, что функция
Предположим, что функция 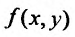 определена в некоторой окрестности
определена в некоторой окрестности 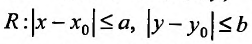 точки
точки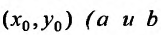 - заданные положительные числа) и удовлетворяет в ней следующим двум условиям:
- заданные положительные числа) и удовлетворяет в ней следующим двум условиям:
- Функция
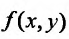 непрерывна и. следовательно, ограничена т. е.
непрерывна и. следовательно, ограничена т. е.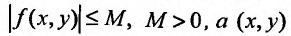 - любая точка
- любая точка 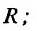
- Функция
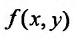 имеет ограниченную частную производную по
имеет ограниченную частную производную по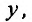 т. е.
т. е.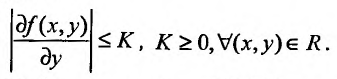
Тогда уравнение (22.4.1) имеет единственное решение 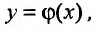 удовлетворяющее начальному условию
удовлетворяющее начальному условию 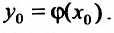 Это решение определено и непрерывно дифференцируемо в интервале
Это решение определено и непрерывно дифференцируемо в интервале 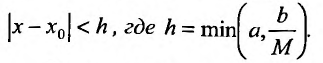 В последующих параграфах рассмотрим частные виды дифференциальных уравнений первого порядка, интегрирование которых сводится к вычислению неопределенных интегралов (или их интегрирование приводится к квадратурам).
В последующих параграфах рассмотрим частные виды дифференциальных уравнений первого порядка, интегрирование которых сводится к вычислению неопределенных интегралов (или их интегрирование приводится к квадратурам).
Дифференциальные уравнения с разделяющимися переменными
Рассмотрим уравнение вида (22.3.1) записанное в дифференциальной форме:
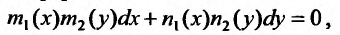 (23.1.1)
(23.1.1)
в котором коэффициенты при 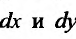 представляют собой произведения функций от
представляют собой произведения функций от 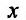 на функции от
на функции от 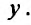 Такое уравнение называется уравнением с разделяющимися переменными. Относительно функций
Такое уравнение называется уравнением с разделяющимися переменными. Относительно функций 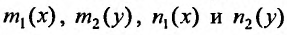 будем предполагать, что они непрерывны при всех рассматриваемых значениях
будем предполагать, что они непрерывны при всех рассматриваемых значениях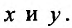 Разделим это равенство на произведение
Разделим это равенство на произведение 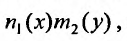 получим уравнение:
получим уравнение: 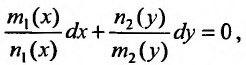
(23.1.2) которое называется уравнением с разделенными переменными, так как коэффициент при 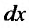 зависит только от
зависит только от 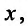 а коэффициент при
а коэффициент при
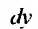 зависит только от
зависит только от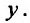 Интегрируя уравнение (23.1.2), получаем выражение:
Интегрируя уравнение (23.1.2), получаем выражение:
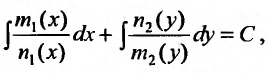
где С = const, называемое общим решением уравнения (23.1.1) в неявном виде (общим интегралом).
Пример №3
Проинтегрировать уравнение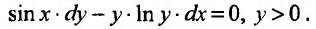
Решение:
Заданное дифференциальное уравнение является уравнением с разделяющимися переменными, так как при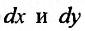 записаны функции, зависящие от
записаны функции, зависящие от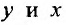 соответственно. Разделим каждый член уравнения на произведение множителей
соответственно. Разделим каждый член уравнения на произведение множителей 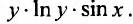 Получим уравнение с разделенными переменными:
Получим уравнение с разделенными переменными: 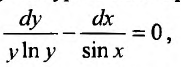 интегрируя которое, последовательно получаем:
интегрируя которое, последовательно получаем:
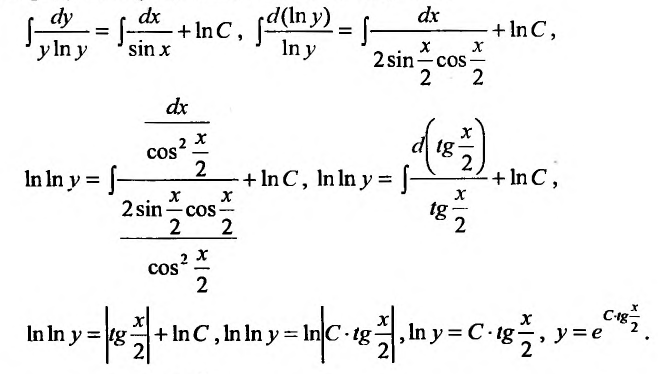
Функция 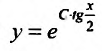 определяет общее решение заданного уравнения. При делении на произведение
определяет общее решение заданного уравнения. При делении на произведение 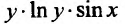 мы можем потерять решение заданного уравнения. Поэтому проверим, являются ли решения
мы можем потерять решение заданного уравнения. Поэтому проверим, являются ли решения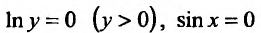 частными решениями. Решение
частными решениями. Решение 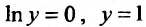 получаем из общего яри
получаем из общего яри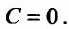 Это означает, что оно является частным решением. Решение sinx = 0 получаем из общего решения, которое можно переписать в виде
Это означает, что оно является частным решением. Решение sinx = 0 получаем из общего решения, которое можно переписать в виде
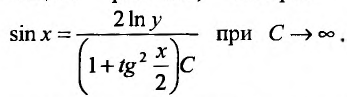
Следовательно, sinx = О также является частным решением заданного уравнения.
Заметим, что уравнение с разделяющимися переменными является одним из основных типов уравнения первого порядка, разрешенных относительно производной и допускающих интегрирование в квадратурах.
Пример №4
Предположим что, эластичность объема валовой продукции 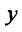 от объема капитальных вложений
от объема капитальных вложений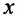 выражается формулой:
выражается формулой:
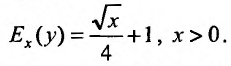
Определить зависимость объема валовой продукции у от объема капитальных вложений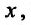 если при
если при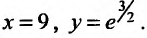
Решение:
Указанная в примере эластичность описывается, как легко следует из определения эластичности функции, дифференциальным уравнением с разделяющимися переменными:
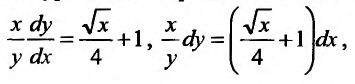 так как при dy записано произведение
так как при dy записано произведение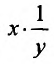 функций, зависящих от
функций, зависящих от 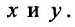 Разделив левую и правую части на
Разделив левую и правую части на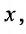 получим уравнение:
получим уравнение:
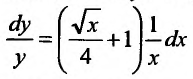 с разделенными переменными, интегрируя которое, последовательно, получим:
с разделенными переменными, интегрируя которое, последовательно, получим:
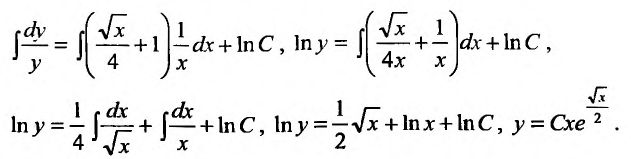
Функция 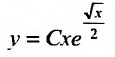 определяет общее решение. Определим значение произвольной постоянной С воспользовавшись начальными условиями. Подставим в общее решение
определяет общее решение. Определим значение произвольной постоянной С воспользовавшись начальными условиями. Подставим в общее решение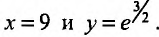 Получим равенство:
Получим равенство:
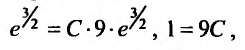
откуда находим 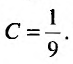 Подставив значение С в общее решение получим функцию
Подставив значение С в общее решение получим функцию 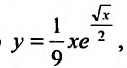 которая описывает зависимость объема валовой продукции
которая описывает зависимость объема валовой продукции 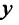 от объема капитальных вложений
от объема капитальных вложений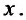
Линейные уравнения
Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции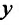 и ее производной
и ее производной 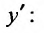
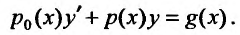 (23.2.1)
(23.2.1)
Коэффициент при у',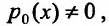 ибо в противном случае (23.2.1) не является дифференциальным уравнением.
ибо в противном случае (23.2.1) не является дифференциальным уравнением.
Приведем уравнение (23.2.1) к каноническому виду. Для этого разделим все члены уравнения на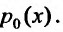 Обозначим полученные отношения
Обозначим полученные отношения 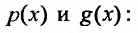
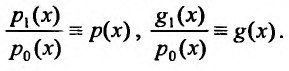
Тогда уравнение (23.2.1) примет вид: 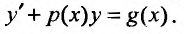 (23.2.2) Умножая левую и правую часть уравнения (23.2.2) на множитель, получатель, называемый интегрирующим,
(23.2.2) Умножая левую и правую часть уравнения (23.2.2) на множитель, получатель, называемый интегрирующим, 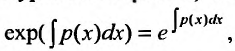 получаем в левой части производную произведения функций:
получаем в левой части производную произведения функций: 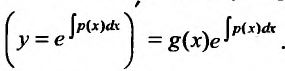 Интегрируя это равенство, найдем общее решение уравнения (23.2.2) в виде:
Интегрируя это равенство, найдем общее решение уравнения (23.2.2) в виде: 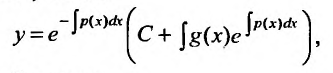 где С = const.
где С = const.
Пример №5
Проинтегрировать уравнение 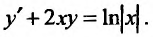
Решение:
Заданное уравнение является линейным уравнением первого порядка. Умножая его на интегрирующий множитель
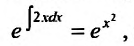 получим:
получим: 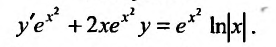 Применив к левой части уравнения формулу производной произведения, преобразуем уравнение к виду:
Применив к левой части уравнения формулу производной произведения, преобразуем уравнение к виду: 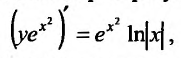 интегрируя которое находим общее решение:
интегрируя которое находим общее решение:
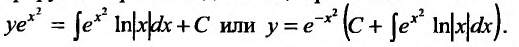
Заметим, что интегрирование линейного дифференциального уравнения можно производить при помощи замены 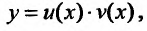
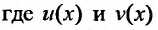 - неизвестные функции. Действительно, подставляя в уравнение (23.2.1)
- неизвестные функции. Действительно, подставляя в уравнение (23.2.1) 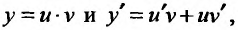 получим:
получим: 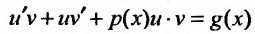 или
или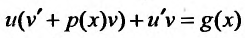 и, выбирая функцию
и, выбирая функцию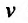 такой, чтобы
такой, чтобы 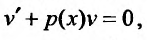 получаем дифференциальное уравнение
получаем дифференциальное уравнение 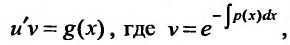 с разделяющимися переменными, интегрирование которого показано в пункте 23.1.
с разделяющимися переменными, интегрирование которого показано в пункте 23.1.
Пример №6
Предположим, что размер предложения сельскохозяйственного продукта в 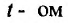 году есть функция цены в
году есть функция цены в 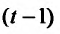 году:
году: 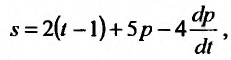 а спрос на этот продукт является функцией цены в данном
а спрос на этот продукт является функцией цены в данном 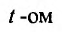 году:
году:
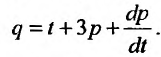 Определить цену равновесия, т. е. когда спрос равен предложению: s = q.
Определить цену равновесия, т. е. когда спрос равен предложению: s = q.
Решение:
По условию примера приравниваем функцию цены к функции предложения:
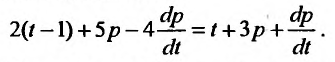
Приведя подобные, получаем линейное дифференциальное уравнение:
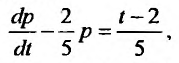
которое проинтегрируем подстановкой 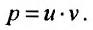 Подставляя
Подставляя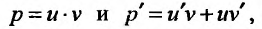 и производя элементарные преобразования, получим уравнение вида:
и производя элементарные преобразования, получим уравнение вида: 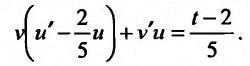 (23.2.3) Определим функцию
(23.2.3) Определим функцию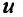 такой, чтобы
такой, чтобы 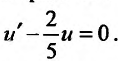 (23.2.4)
(23.2.4)
Уравнение (23.2.4) - уравнение с разделяющимися переменными. Его частным решением является функция: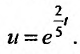 В качестве решения уравнения с разделяющимися переменными (23.2.4), выбирается функция, аналитическая запись которой самая простая.
В качестве решения уравнения с разделяющимися переменными (23.2.4), выбирается функция, аналитическая запись которой самая простая.
Представляя найденное значение функции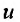 в (23.2.3), снова получаем дифференциальное уравнение с разделяющимися переменными:
в (23.2.3), снова получаем дифференциальное уравнение с разделяющимися переменными:
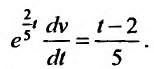 Запишем его в дифференциальной форме:
Запишем его в дифференциальной форме: 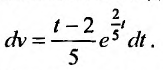 Интегрируя левую и правую часть этого уравнения, получим его общее решение:
Интегрируя левую и правую часть этого уравнения, получим его общее решение: 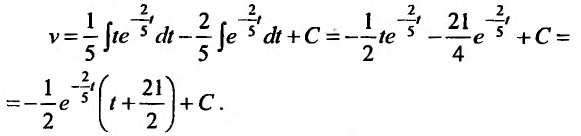
Тогда общее решение заданного уравнения записывается в виде: 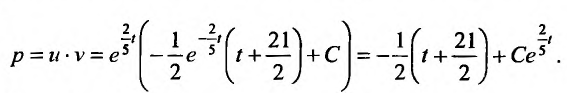
Замечание. Линейные уравнения вида: 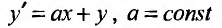 приводятся к уравнениям с разделяющимися переменными при помощи замены
приводятся к уравнениям с разделяющимися переменными при помощи замены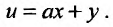
Действительно, 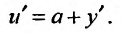 Тогда исходное уравнение примет вид
Тогда исходное уравнение примет вид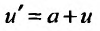 или
или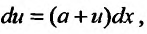 а это и есть дифференциальное уравнение с разделяющимися переменными.
а это и есть дифференциальное уравнение с разделяющимися переменными.
Уравнения Бернулли
Обобщением линейного дифференциального уравнения первого порядка является уравнение Бернулли: 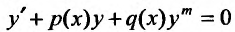 (23.3.1)
(23.3.1)
причем показатель степени 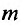 можно считать отличным от нуля и единицы, так как в этих случаях уравнение будет линейным. Разделим каждый член уравнения (23.3.1) на
можно считать отличным от нуля и единицы, так как в этих случаях уравнение будет линейным. Разделим каждый член уравнения (23.3.1) на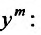
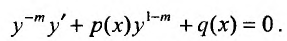 (23.3.2)
(23.3.2)
Введем новую искомую функцию 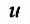 по формуле:
по формуле:
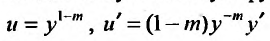 (23.3.3)
(23.3.3)
После подстановки в (23.3.2) выражений (23.3.3), уравнение
(23.3.2) примет вид:
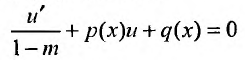
или
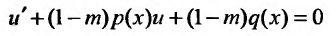
или
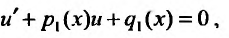 (23.3.4)
(23.3.4)
где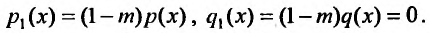
Уравнение (23.3.4) линейное относительно искомой функции 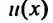 и оно интегрируется аналогично уравнению (23.2.2).
и оно интегрируется аналогично уравнению (23.2.2).
Пример №7
Проинтегрировать уравнение: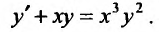
Решение:
Данное уравнение является уравнением Бернулли. Показатель степени 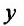 в правой части равен двум:
в правой части равен двум: 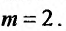 . Разделим обе части заданного уравнения на
. Разделим обе части заданного уравнения на 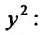
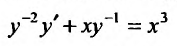
и введем новую искомую функцию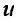 по формуле:
по формуле: 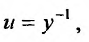
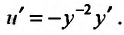
При этом уравнение приведется к виду:
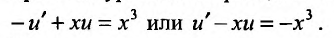
Полученное уравнение является линейным относительно новой искомой функции 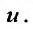 Умножая его на интегрирующий множитель
Умножая его на интегрирующий множитель 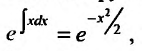
получаем в левой части производную произведения функций: 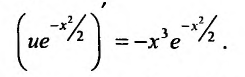 Интегрируя обе части полученного уравнения, будем иметь:
Интегрируя обе части полученного уравнения, будем иметь:
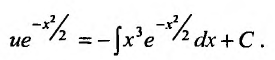 Для вычисления интеграла в правой части равенства, применим формулу интегрирования по частям:
Для вычисления интеграла в правой части равенства, применим формулу интегрирования по частям: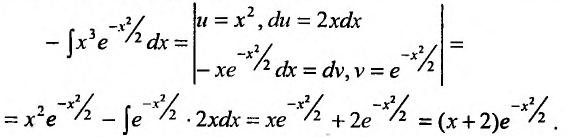
Подставив значение интеграла, получим:
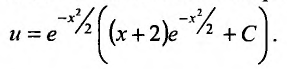 Выполнив обратную замену
Выполнив обратную замену 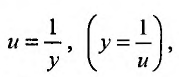 находим общее решение заданного уравнения в виде:
находим общее решение заданного уравнения в виде:
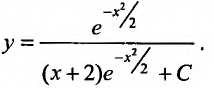
Однородные дифференциальные уравнения и приводящиеся к ним
Определение 23.4.1. Однородной функцией степени 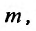 называется функция
называется функция 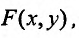 если
если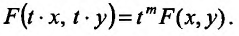
Пологая 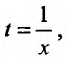 получим
получим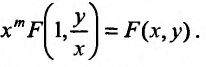
Определение 23.4.2. Дифференциальное уравнение вида
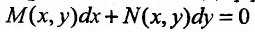 (23.4.1)
(23.4.1)
называется однородным, если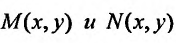 однородные функции степени
однородные функции степени 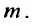
В силу однородности функций 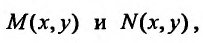 уравнение (23.4.1) можно записать в виде:
уравнение (23.4.1) можно записать в виде: 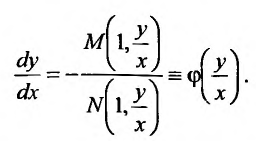
(23.4.2) Выполняя в (23.4.2) подстановку: 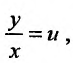 или
или
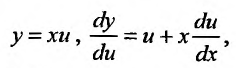
получим
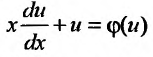 или
или 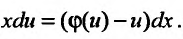 (23.4.3)
(23.4.3)
Это уравнение с разделяющимися переменными. Разделяя в уравнении (23.4.3) переменные и интегрируя, найдем его общее решение:
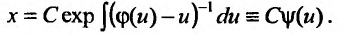
Возвращаясь к старой переменной, семейство интегральных кривых запишем в виде: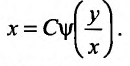 (23.4.4)
(23.4.4)
Из (23.4.4) следует, что все интегральные кривые однородного уравнения могут быть получены из одной интегральной кривой при помощи преобразования подобия с центром подобия в начале координат: 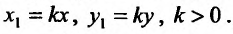
Пример №8
Проинтегрировать дифференциальное уравнение:
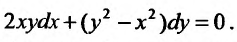
Решение:
Заданное уравнение записано в дифференциальной форме, где 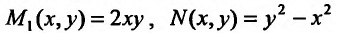 однородные функции второй степени. Следовательно, заданное уравнение однородное. Разрешим его относительно производной
однородные функции второй степени. Следовательно, заданное уравнение однородное. Разрешим его относительно производной 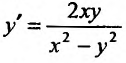 и разделим числитель и знаменатель правой части на
и разделим числитель и знаменатель правой части на 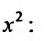
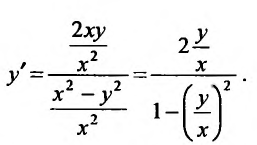
Подставив 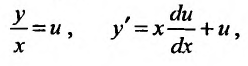 получим уравнение:
получим уравнение: 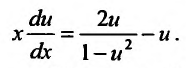 Приведя к общему знаменателю в правой части, получим уравнение с разделяющимися переменными:
Приведя к общему знаменателю в правой части, получим уравнение с разделяющимися переменными: 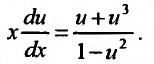 (23.4.5) Разделив в (23.4.5) переменные, преобразуем его к уравнению с разделенными переменными:
(23.4.5) Разделив в (23.4.5) переменные, преобразуем его к уравнению с разделенными переменными: 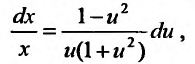 проинтегрировав которое, найдем общее решение в виде:
проинтегрировав которое, найдем общее решение в виде: 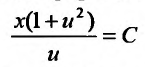 или, возвращаясь к у, получим:
или, возвращаясь к у, получим: 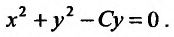
Это окружности, проходящие через начало координат, центры которых лежат на оси Оу, касающиеся оси Ох в точке (0,0).
К однородному дифференциальному уравнению преобразуется также уравнение 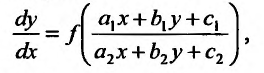 (23.4.6)
(23.4.6)
если 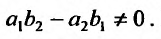 Если же
Если же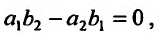 то (23.4.6) преобразуется к уравнению с разделяющимися переменными. Покажем это. Для этого введем новые переменные по формулам:
то (23.4.6) преобразуется к уравнению с разделяющимися переменными. Покажем это. Для этого введем новые переменные по формулам: 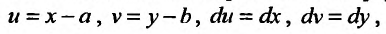 где
где 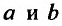 удовлетворяют системе алгебраических уравнений:
удовлетворяют системе алгебраических уравнений:
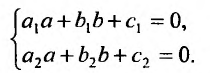
Тогда, если 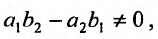 то получим однородное уравнение
то получим однородное уравнение
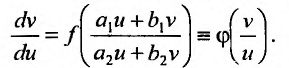
Если же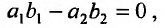 то
то 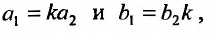 и уравнение (23.4.6) примет вид:
и уравнение (23.4.6) примет вид: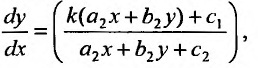
которое подстановкой 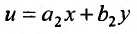 приводится к уравнению с разделяющимися переменными:
приводится к уравнению с разделяющимися переменными: 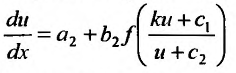
К однородному уравнению приводится также уравнение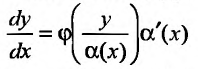 подстановкой
подстановкой 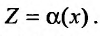
Пример №9
Предположим, что динамическая функция предложения товара описывается зависимостью: 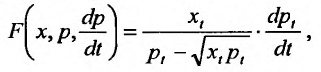 где х, - запас товара,
где х, - запас товара,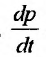 — - тенденция формирования цены, р, - цена товара в данный момент времени t. Требуется определить зависимость цены от количества товара, если динамическая функция предложения товара будет равна скорости увеличения запаса товара.
— - тенденция формирования цены, р, - цена товара в данный момент времени t. Требуется определить зависимость цены от количества товара, если динамическая функция предложения товара будет равна скорости увеличения запаса товара.
Решение:
Из условия примера следует, что динамическая функция предложения товара равна скорости увеличения запаса товара, т.е. 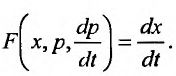
Подставив выражение для динамической функции предложения товара, получим уравнение:
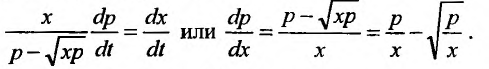 Это однородное дифференциальное уравнение, которое интегрируем при помощи подстановки
Это однородное дифференциальное уравнение, которое интегрируем при помощи подстановки 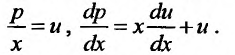 Выполнив подстановку, получим уравнение с разделяющимися переменными:
Выполнив подстановку, получим уравнение с разделяющимися переменными:
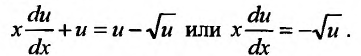 Разделив переменные
Разделив переменные 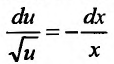
и вычислив интегралы от обеих частей уравнения с разделенными переменными, найдем общее решение в виде:
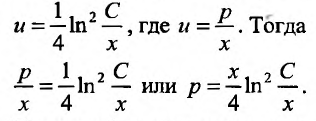
Получим функцию цены р в зависимости от запаса товара 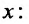
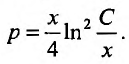
Дифференциальное уравнение в полных дифференциалах
Дифференциальное уравнение вида:
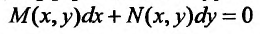 (23.5.1)
(23.5.1)
называется уравнением в полных дифференциалах, если существует такая функция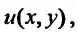 что
что
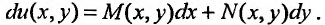 (23.5.2)
(23.5.2)
Тогда (23.5.2) можно переписать в виде: 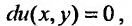 откуда находим общее решение в неявном виде:
откуда находим общее решение в неявном виде: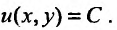
Отметим, что необходимым и достаточным условием существования функции 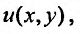 удовлетворяющей условию (23.5.2), является равенство:
удовлетворяющей условию (23.5.2), является равенство:
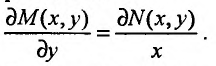 (23 5 3)
(23 5 3)
Пример №10
Проинтегрировать дифференциальное уравнение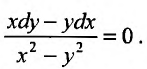
Решение:
Для данного уравнения выполняется условие (23.5.2) во всей плоскости, кроме точки (0,0). Легко заметить, что функция 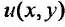 имеет вид:
имеет вид: 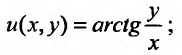 и, следовательно, заданное уравнение можно записать в виде:
и, следовательно, заданное уравнение можно записать в виде:
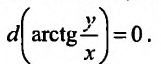
Тогда общее решение имеет вид:
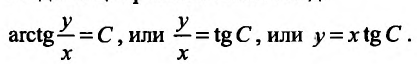
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |