Системы дифференциальных уравнений - определение и вычисление с примерами решения

Содержание:

Общие понятия о системе дифференциальных уравнений:

Определение 26.1.1. Системой обыкновенных дифференциальных уравнений называется выражение вида: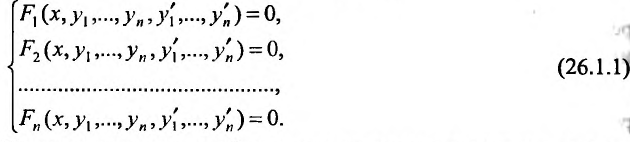

Частным случаем такой системы является нормальная система (разрешенная относительно производных) дифференциальных уравнений: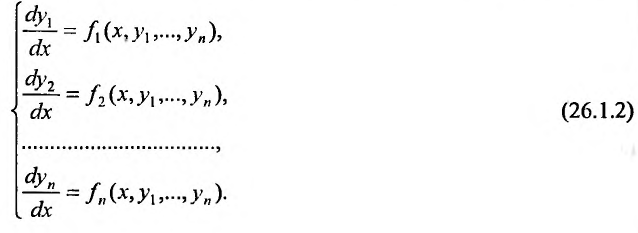

Система (26.1.2) задана в области 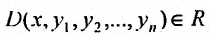, если в каждой точке этой области определены функции

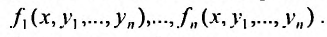
Совокупность функций

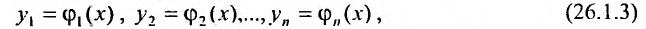
заданных, на промежутке 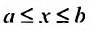, называется решением системы (26.1.2), если эти функции тождественно удовлетворяют уравнениям (26.1.2):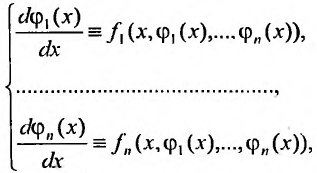

при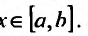

Задача Коши формулируется следующим образом: найти решение (26.1.3) системы (26.1.2) , удовлетворяющее условиям: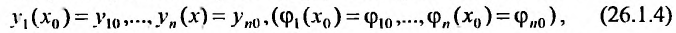

где точка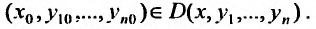 Следовательно, задача Коши состоит в том, чтобы найти решение, проходящее через точку

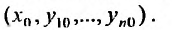
Совокупность n функций:

называется общим решением системы (26.1.2) в области D, если для любой точки 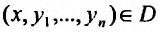система равенств (26.1.5), разрешима относительно произвольных постоянных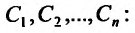

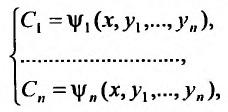
и при этих значениях 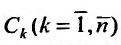функции (26.1.5) тождественно удовлетворяют уравнениям (26.1.2).

Из общего решения (26.1.5) получаем частные решения вида (26.1.3) при фиксированных значениях постоянных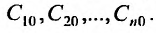 Заметим, что любое уравнение n -го порядка

можно записать как систему вида (26.1.2), применив следующий прием:

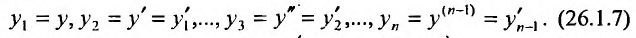Тогда для уравнения 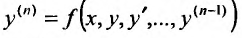получим систему дифференциальных уравнений:

эквивалентную уравнению (26.1.6).

При такой записи функция 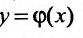является решением дифференциального уравнения n -го порядка. В самом деле, пусть 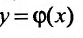решение уравнения (26.1.6). Тогда,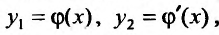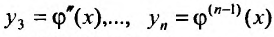, согласно (26.1.7), есть решение системы (26.1.8). И, обратно, пусть 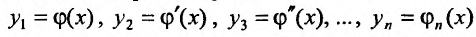есть решение системы (26.1.8). Тогда 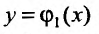есть решение уравнения (26.1.6) , так как согласно (26.1.8) будем иметь 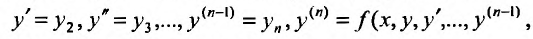что и доказывает утверждение.

И для системы уравнений (26.1.2) иногда можно сопоставить эквивалентное одно уравнение с одной неизвестной функцией, путем последовательного дифференцирования, например, первого уравнения по х и выражая функции 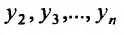из других уравнений.

Пример:

Дифференциальное уравнение третьего порядка 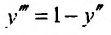запишем в виде системы третьего порядка.

Решение:

Положим 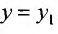тогда система будет иметь вид:

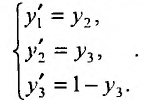
Пример:

Систему двух дифференциальных уравнений 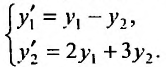сведем к дифференциальному уравнению.

Решение:

Продифференцируем первое из уравнений системы по x

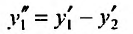
и значение 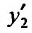подставим из второго уравнения системы:

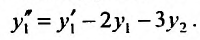
Из первого уравнения заданной системы найдем :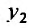

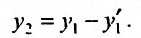
Подставляя это значение 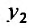в полученное равенство, получим: 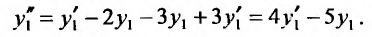Итак, уравнение, эквивалентное системе, имеет вид: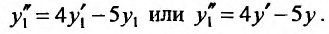

Ниже мы остановимся на изучении систем линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Способы решения систем линейных дифференциальных уравнений второго порядка с постоянными коэффициентами

Система двух дифференциальных уравнений относительно неизвестных 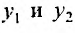заданных для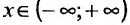вида

где 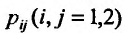- постоянные, называется линейной однородной

системой с постоянными коэффициентами.

Система (26.2.1) всегда может быть решена в элементарных функциях: полиномах, показательных и тригонометрических функциях. При этом можно выделить два случая.

1. 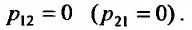. Если 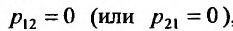, то система примет вид:

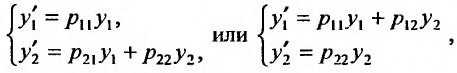
в которой первое (второе) уравнение имеет решение: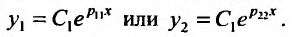

Подставляя это решение во второе (первое) уравнение, получим линейное дифференциальное уравнение первого порядка:

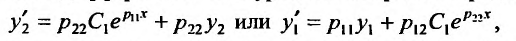
которое интегрируется, например, при помощи интегрирующего множителя:

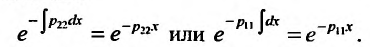
В результате получаем общее решение системы (26.2.1) при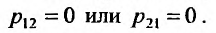

Пример:

Решить систему

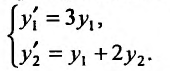
Решение:

Первое уравнение системы является дифференциальным уравнением первого порядка с разделяющимися переменными. Поэтому, последовательно преобразовывая и интегрируя, получим:

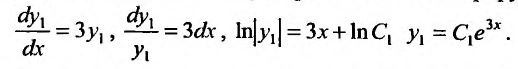
Подставим найденное значение 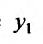во второе уравнение системы, получим линейное уравнение:

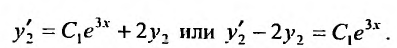
Умножим это уравнение на интегрирующий множитель 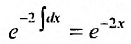огда в левой части уравнения будет записана производная произведения: 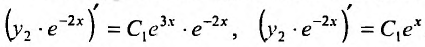Вычисляя интегралы обеих частей последнею уравнения, найдем его общее решение

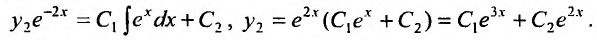
Таким образом, общее решение системы будет иметь вид:

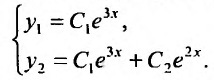
2. Пусть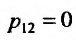. Тогда систему (26.2.1) можно свести к одному дифференциальному уравнению второго порядка с постоянными коэффициентами. Для этого продифференцируем первое уравнение системы и подставим из второго уравнения значение 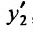, а затем и значение 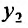, из первого уравнения системы. В результате получим однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, относительно 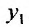, которое решаем известными методами, изложенными в лекции 25. Затем находим 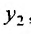используя первое уравнение системы.

Итак, дифференцируем первое уравнение по х:

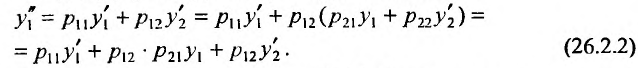
Из первого уравнения системы (26.2.1) находим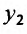

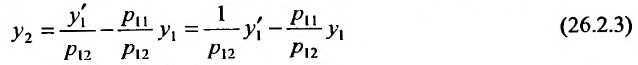
и подставляем в (26.2.2):

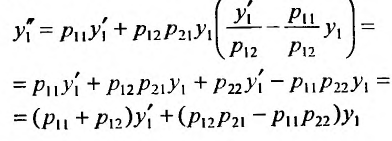
или

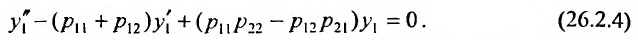
Уравнение (26.2.4)- это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами, общее решение которого зависит от корней характеристическою уравнения:

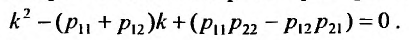Если 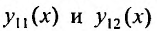- частные решения (26.2.4), то общее решение имеет вид:

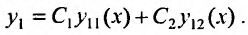
Вторую функцию 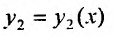можно найти из дифференциального уравнения первого порядка:

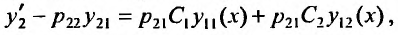которое решается при помоши интегрирующего множителя, или, что проще, из равенства (26.2.3):

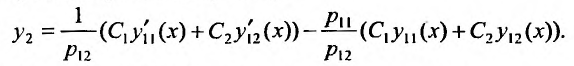
Пример:

Найти общее решение системы: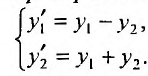-и решить задачу Коши (0;1;0).

Решение:

Продифференцируем первое уравнение системы и подставим значение 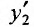из второго уравнения заданной системы:

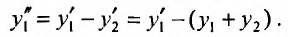
В полученное уравнение подставим значение 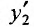из первого уравнения:

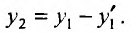Получим:

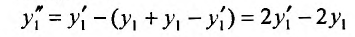
или

(26.2.4)- линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Для нахождения его общего решения составим характеристическое уравнение: 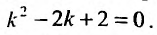. Его корни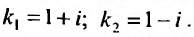

Тогда общее решение уравнения (26.2.4) имеет вид:

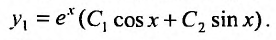
Подставляя в равенство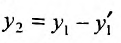 найденное значение 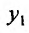и производную 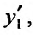последовательно получим:

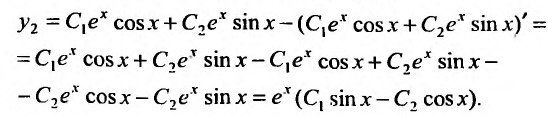
Итак, общее решение системы имеет вид:

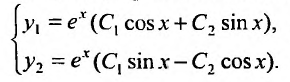
Применение систем дифференциальных уравнений в исследовании проблем экономического роста

Предложенная В. Леонтьевым динамическая межотраслевая модель является классическим примером использования дифференциальных уравнений в исследовании проблем экономического роста. Построение этой модели удобно представить как дезагрегирование элементов простейшей динамической модели воспроизводства общественного продукта, при котором эндогенные и экзогенные макропеременные заменяются векторами, а технологические макропараметры - матрицами. Модель имеет вид:

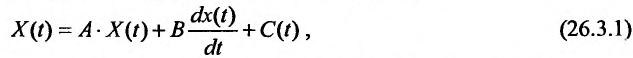
где 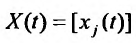- матрица-столбец объемов производсгва;

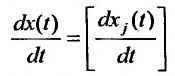матрица-столбец абсолютных приростовм производства

C(t) - матрица-столбец потребления (включая непроизводственные накопления);

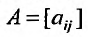- матрица коэффициентов прямых материальных затрат, которые включают затраты на возмещение выбытия и капитальный ремонт основных производственных фондов;

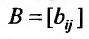- матрица коэффициентов капиталоемкости приростов

(затраты производственного накопления на единицу прироста соответствующих видов продукции).

Пусть C(t) = 0, тогда систему (26.3.1) последовательно преобразуем к виду: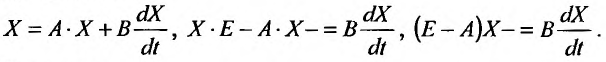

Положим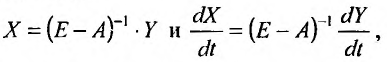

тогда получим систему вида:

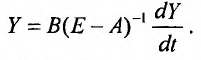
Умножая на обратную матрицу 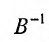, а затем на матрицу (Е - А), получим систему однородных дифференциальных уравнений:

решения которой, характеризуют предельные технологические возможности развития производства при заданных матрицах А и В, когда все ресурсы национального дохода направляются на расширенное воспроизводство, а потребление остается неизменным, т.е. С(0) = 0.

Так как мы изучали системы вида (26.2.1), то рассмотрим систему (26.3.2) для народного хозяйства в разрезе двух отраслей.

• Заказать решение задач по высшей математике

Пусть заданы матрицы:

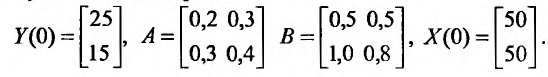
Составим систему вида (26.3.2):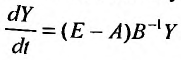

Для этого находим матрицы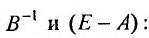

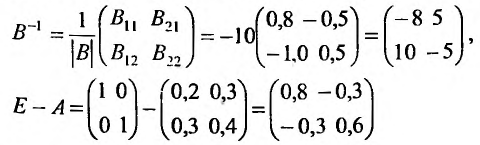и произведение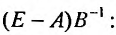

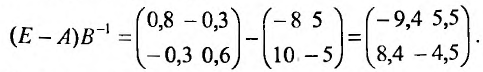Тогда система примет вид:

в которой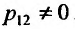Следовательно, имеем второй случай. Дифференцируем первое уравнение системы (26.3.3), подставляем значение 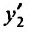из второго уравнения этой системы, затем из первого уравнения подставляем значение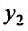

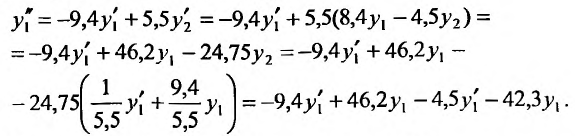
Приведя подобные, окончательно получим:

Составляем характеристическое уравнение: 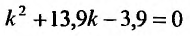и находим его корни:

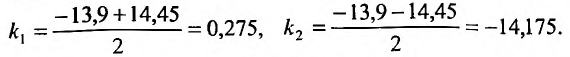
общее решение уравнения (26.3.4) имеет вид:

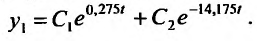
Вторую функцию 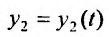найдем из равенства:

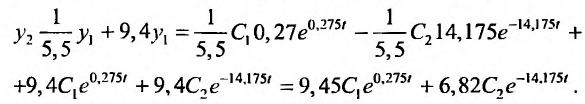
Итак, общее решение системы (26.3.3) имеет вид: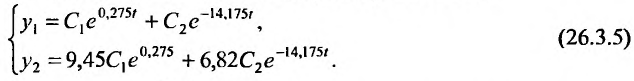 Так как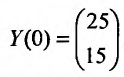то определим значение произвольных постоянных 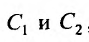, решая систему: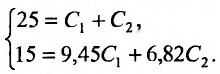

Откуда, получим 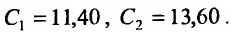Тогда, частное решение системы (26.3.5) примет вид:

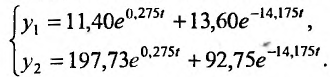
Технологический темп прироста равен 0,275. Второе слагаемое в частном решении очень быстро стремится к нулю. Семейство траекторий (26.3.5) изображено на рисунке 26.1.

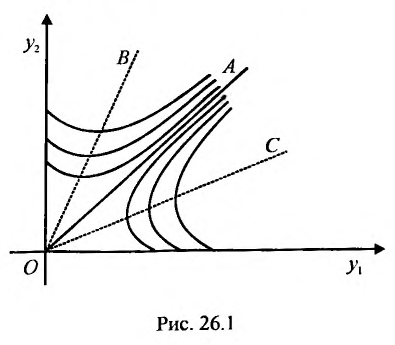
Луч OA - траектория с постоянным темпом прироста национального дохода. Все траектории семейства (26.3.5) также стремятся к лучу OA. Войдя в конус ВОС допустимых решений, траектория уже остается в нем. В теории дифференциальных уравнений семейство траекторий такого типа называют седлом.